1.2 《二次函数的图象》(4)-浙教版数学九年级上册课堂分层训练
试卷更新日期:2025-08-06 类型:同步测试
一、基础应用
-
1. 已知二次函数为 , 则它的图象可能是( ).A、
 B、
B、 C、
C、 D、
D、 2. 将二次函数的图象向左平移1个单位,再向下平移2个单位,所得图象的函数表达式是( )A、 B、 C、 D、3. 已知二次函数的图象开口向下,则的值可以是( )A、 B、0 C、2 D、44. 二次函数()的图象如图所示,则一次函数与一次函数在同一坐标系内的图象大致是( )
2. 将二次函数的图象向左平移1个单位,再向下平移2个单位,所得图象的函数表达式是( )A、 B、 C、 D、3. 已知二次函数的图象开口向下,则的值可以是( )A、 B、0 C、2 D、44. 二次函数()的图象如图所示,则一次函数与一次函数在同一坐标系内的图象大致是( )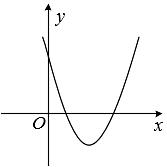 A、
A、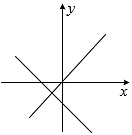 B、
B、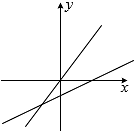 C、
C、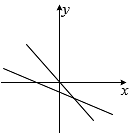 D、
D、 5. 已知一条抛物线的形状、开口方向与抛物线相同,它的顶点坐标为 , 则此抛物线的解析式 .6. 请你写出一个二次函数,其图象满足条件:①开口向下,②顶点在y轴上.此二次函数的解析式可以是 .7. 二次函数y=ax2+bx+c(a≠0)中,决定该函数图象的开口方向和开口大小,在确定的条件下,决定图象对称轴的位置,决定图象与y轴交点的位置.8. 已知函数 是二次函数.(1)、求m的值;(2)、求这个二次函数的解析式,并指出开口方向、对称轴和顶点坐标.9. 已知:抛物线y=﹣x2+bx+c经过点B(﹣1,0)和点C(2,3).(1)、求此抛物线的表达式;(2)、如果此抛物线沿y轴平移一次后过点(﹣2,1),试确定这次平移的方向和距离.
5. 已知一条抛物线的形状、开口方向与抛物线相同,它的顶点坐标为 , 则此抛物线的解析式 .6. 请你写出一个二次函数,其图象满足条件:①开口向下,②顶点在y轴上.此二次函数的解析式可以是 .7. 二次函数y=ax2+bx+c(a≠0)中,决定该函数图象的开口方向和开口大小,在确定的条件下,决定图象对称轴的位置,决定图象与y轴交点的位置.8. 已知函数 是二次函数.(1)、求m的值;(2)、求这个二次函数的解析式,并指出开口方向、对称轴和顶点坐标.9. 已知:抛物线y=﹣x2+bx+c经过点B(﹣1,0)和点C(2,3).(1)、求此抛物线的表达式;(2)、如果此抛物线沿y轴平移一次后过点(﹣2,1),试确定这次平移的方向和距离.二、能力提升
-
10. 已知反比例函数在第二象限内的图象与一次函数的图象如图所示,则函数的图象可能为( )
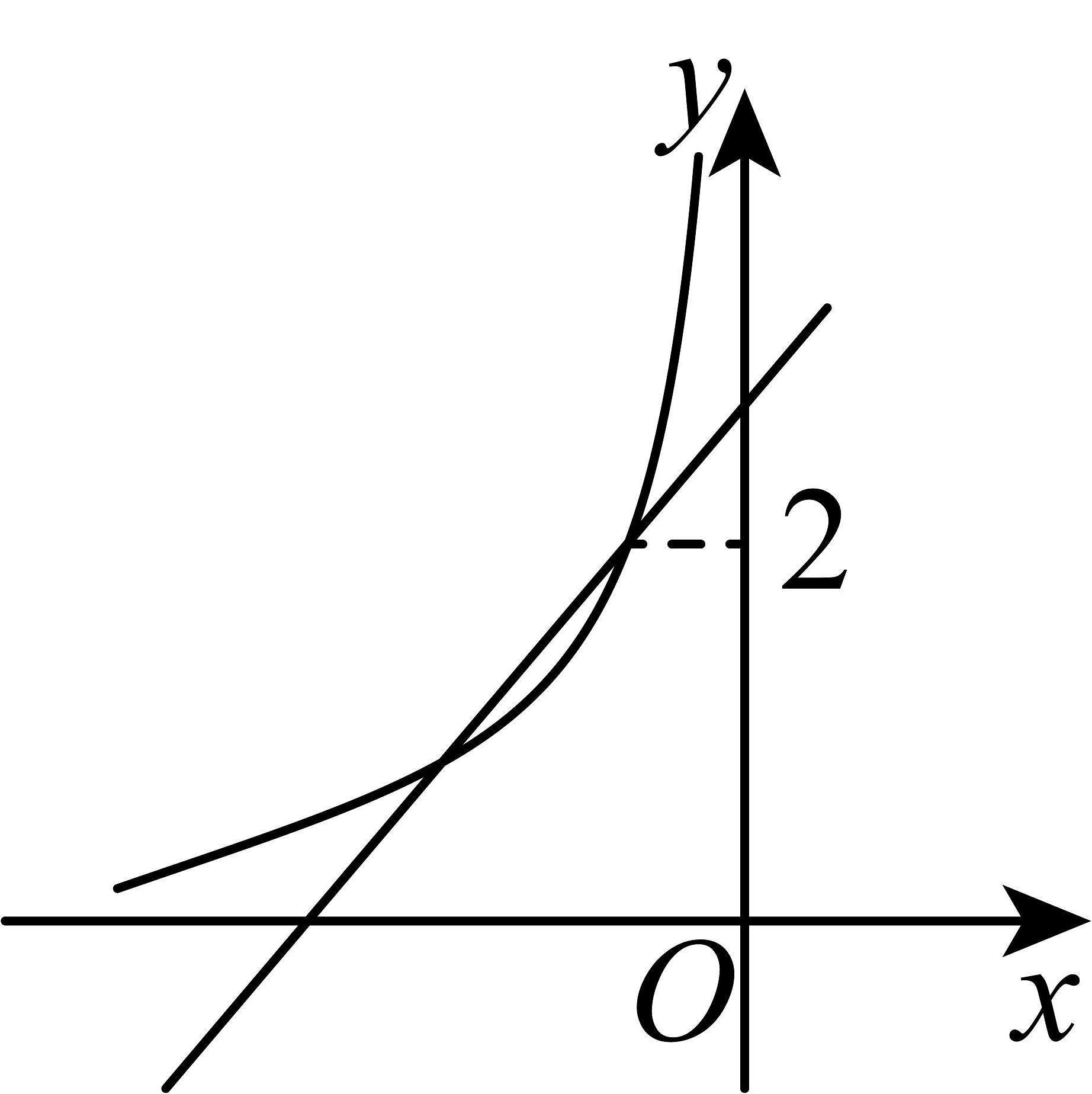 A、
A、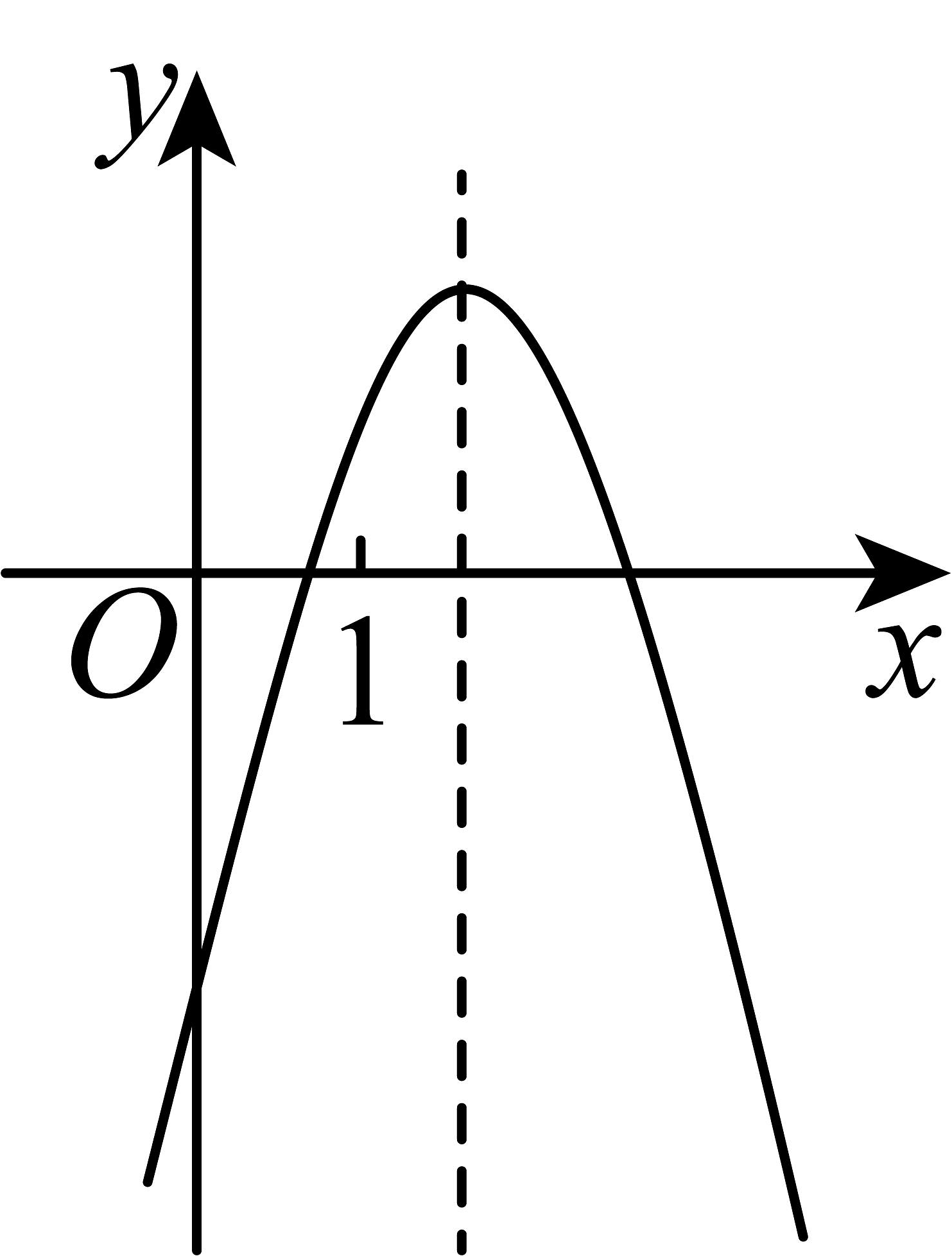 B、
B、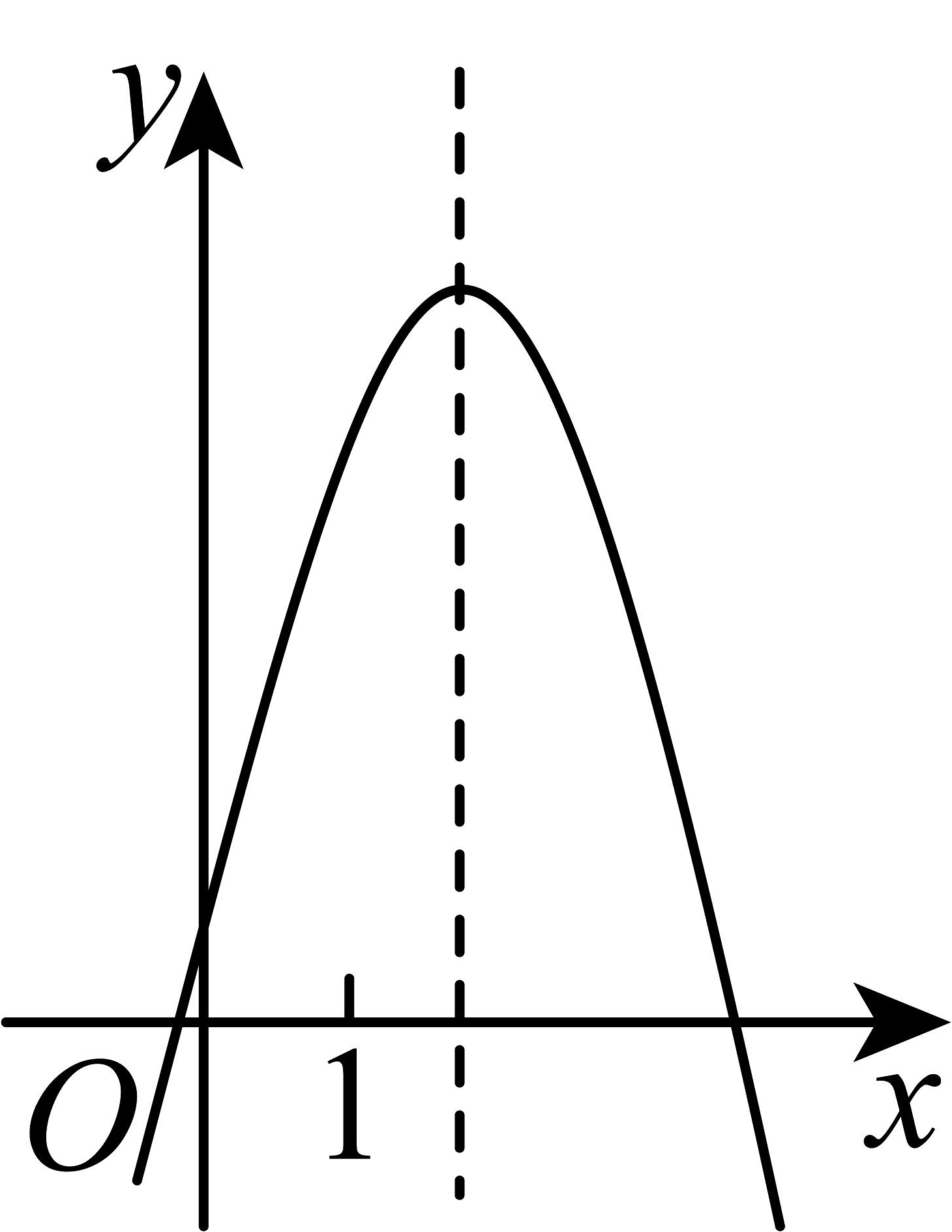 C、
C、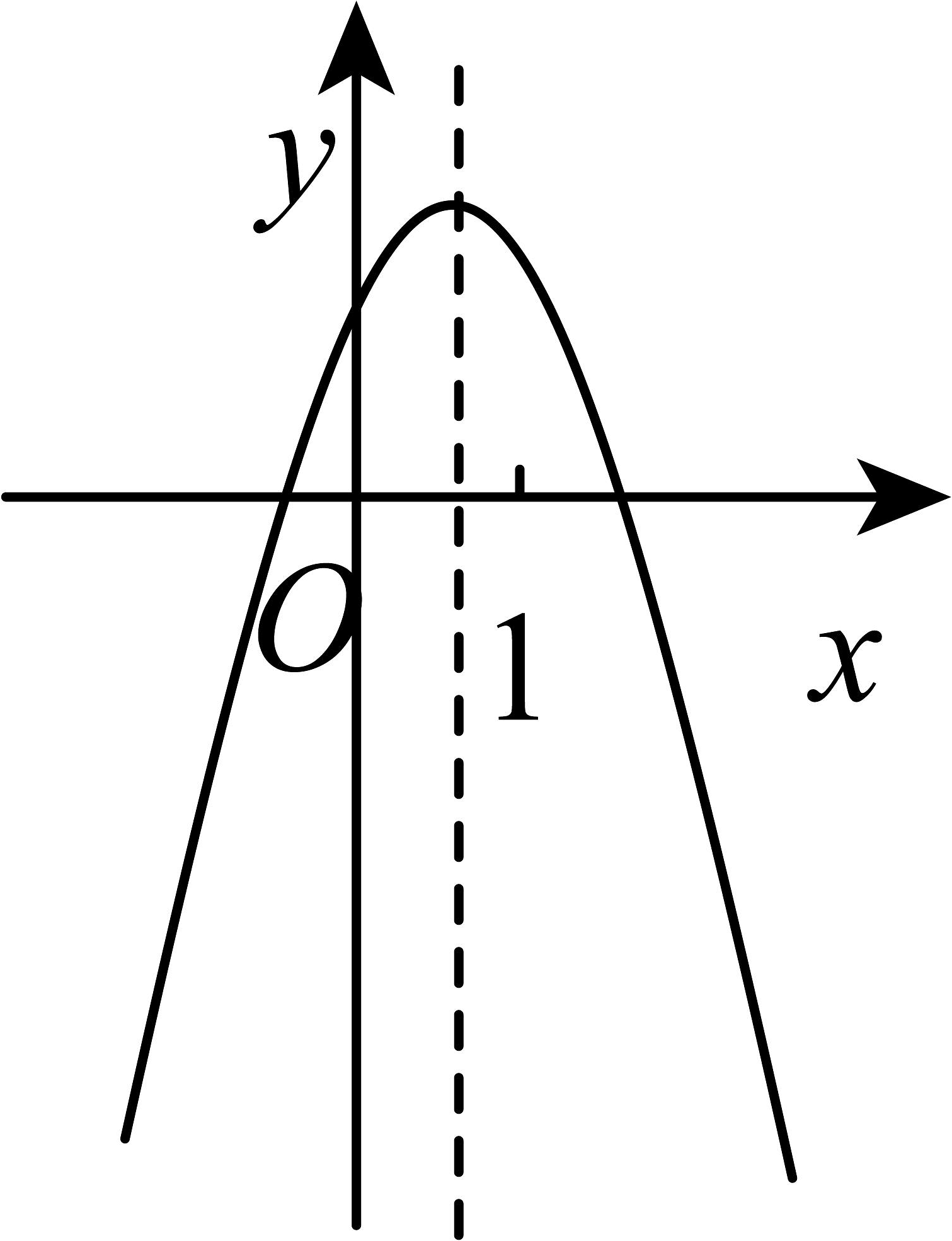 D、
D、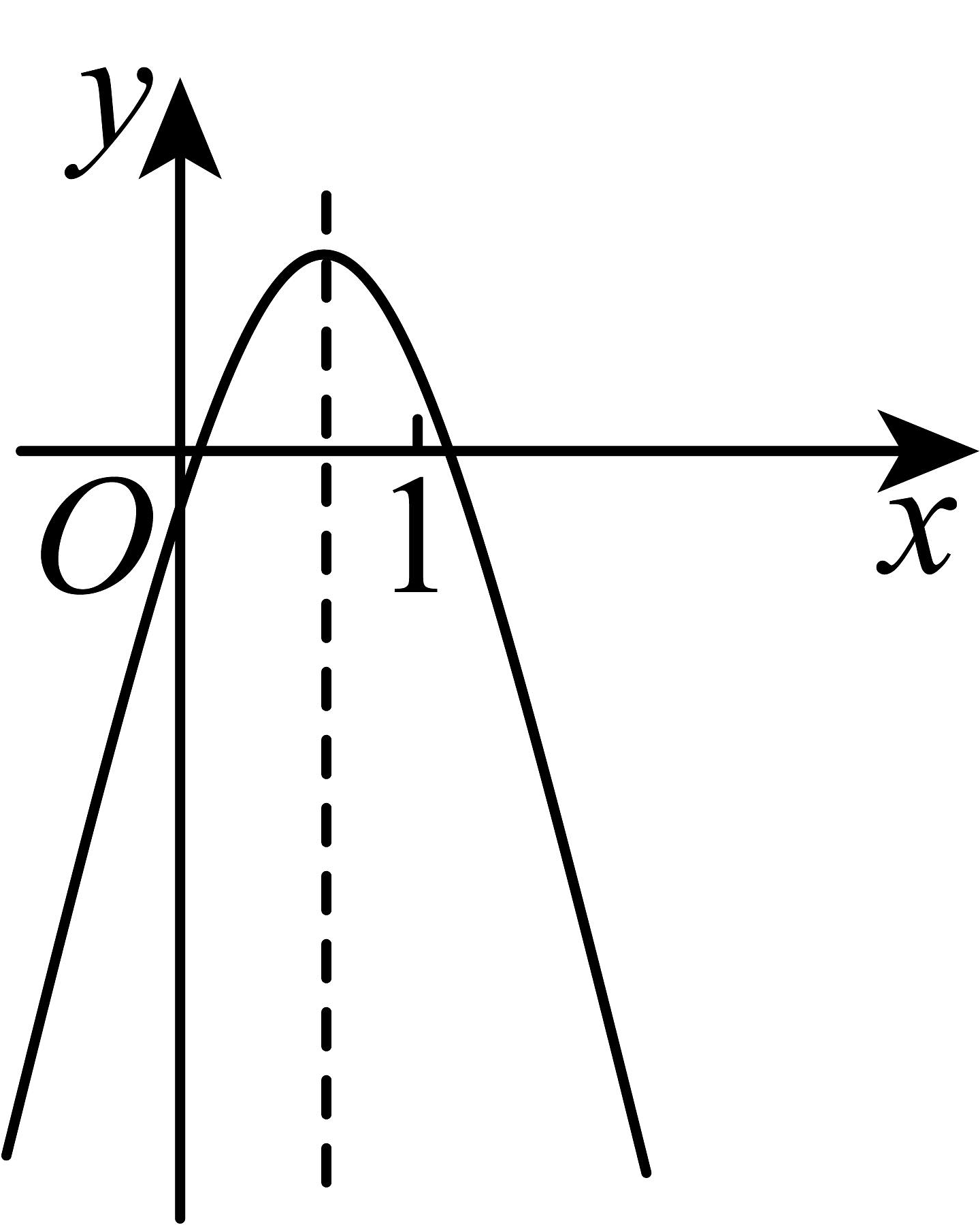 11. 如图,已知抛物线(a、b、c为常数,且)的对称轴为直线 , 且该抛物线与轴交于点 , 与轴的交点在 , 之间(不含端点),则下列结论正确的有多少个( )
11. 如图,已知抛物线(a、b、c为常数,且)的对称轴为直线 , 且该抛物线与轴交于点 , 与轴的交点在 , 之间(不含端点),则下列结论正确的有多少个( )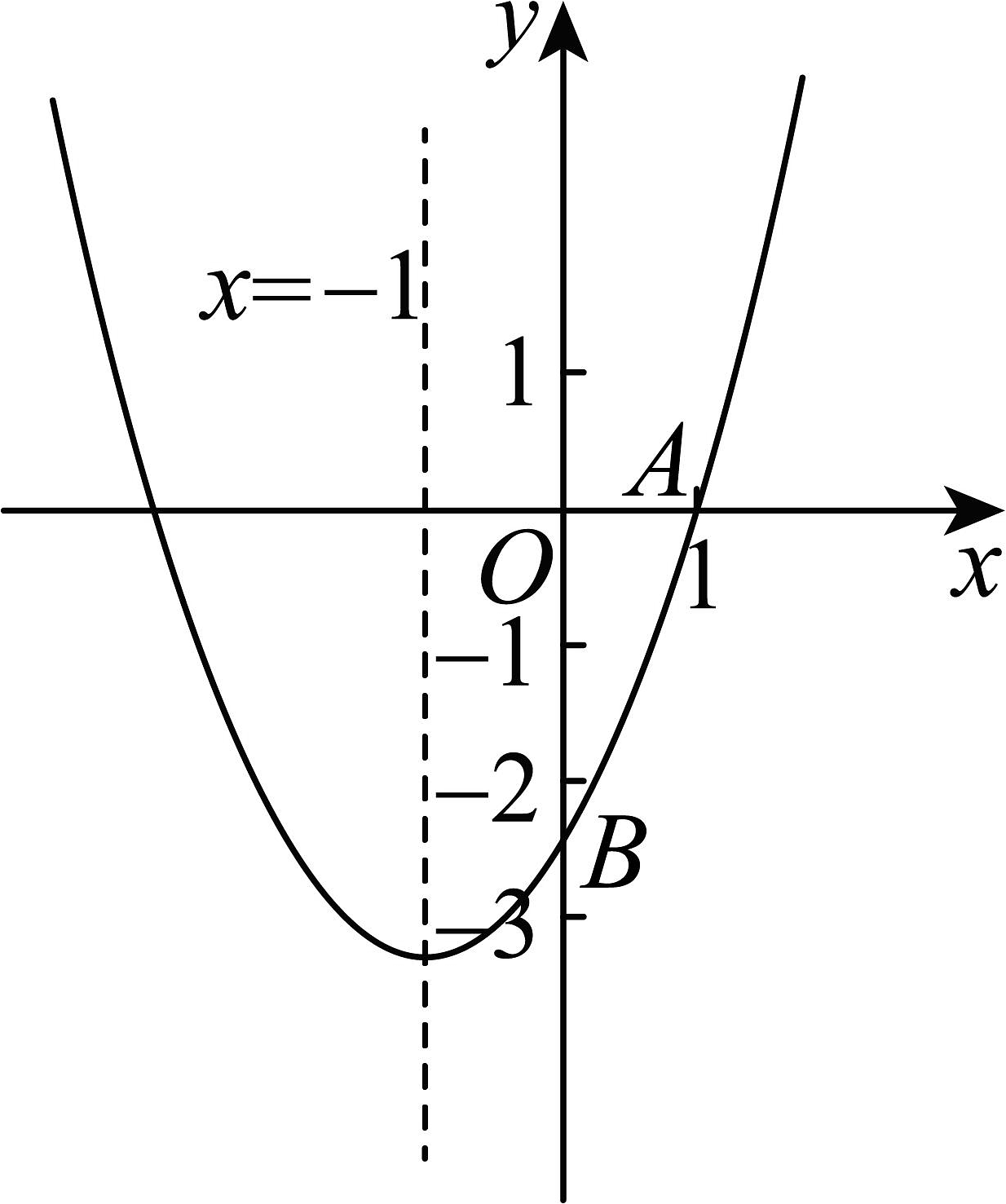
①;
②;
③;
④若方程两根为 , 则 .
A、1 B、2 C、3 D、412. 抛物线的图象如图所示,对称轴为直线: , 下列说法:①;②(t为全体实数);③;④若和为图象上两点,且 , 则 . 其中正确的是( ) A、②③ B、②④ C、③④ D、①②13. 已知二次函数的函数值y和自变量x的部分对应取值如下表所示:
A、②③ B、②④ C、③④ D、①②13. 已知二次函数的函数值y和自变量x的部分对应取值如下表所示:x
…
0
1
2
…
y
…
2
m
2
…
则下列结论:①;②若点 , , 均在该二次函数图象上,则;③若方程的两个实数根为 , , 则;④ . 其中正确的结论是( )
A、①② B、②③ C、③④ D、④14. 已知函数的图象与轴只有一个交点,则 .15. 已知二次函数的图象如图,①;②;③;④;⑤ , 其中结论正确的有(填序号). 16. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=﹣2,并与x轴交于A , B两点.若OA=5OB, 则下列结论中:
16. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=﹣2,并与x轴交于A , B两点.若OA=5OB, 则下列结论中:①abc>0;
②(a+c)2﹣b2=0;
③9a+4c<0;
④若m为任意实数,则am2+bm+2b≥4a , 正确的是 .
 17. 已知抛物线 经过点 .(1)、求 的值.(2)、若 ,过点 作 轴的平行线交抛物线于另一点 ,交 轴于点 ,且 ,求此抛物线的表达式.18. 在平面直角坐标系中,反比例函数与二次函数y=k(x2+x-1)的图象交于点A(1,k)和点B(-1,-k).
17. 已知抛物线 经过点 .(1)、求 的值.(2)、若 ,过点 作 轴的平行线交抛物线于另一点 ,交 轴于点 ,且 ,求此抛物线的表达式.18. 在平面直角坐标系中,反比例函数与二次函数y=k(x2+x-1)的图象交于点A(1,k)和点B(-1,-k).
(1)当k=-2时,求反比例函数的解析式;
(2)要使反比例函数与二次函数都是y随着x的增大而增大,求k应满足的条件以及x的取值范围.
(3)设二次函数的图象的顶点为Q,当△ABQ是以AB为斜边的直角三角形时,求k的值.
三、综合拓展
-
19. 为落实“双减”,老师布置了一项这样的课后作业:

二次函数的图象经过点 , 且不经过第一象限,写出满足这些条件的一个函数表达式.
(1)、 [观察发现]请完成作业,并在直角坐标系中画出大致图象.
(2)、[思考交流]小亮说:“满足条件的函数图象的对称轴一定在y轴的左侧.”
小莹说:“满足条件的函数图象一定在x轴的下方.”
你认同他们的说法吗?若不认同,请举例说明.
(3)、[概括表达]小博士认为这个作业的答案太多,老师不方便批阅,于是探究了二次函数的图象与系数a,b,c的关系,得出了提高老师作业批阅效率的方法.
请你探究这个方法,写出探究过程.
20. 如图1,抛物线y=ax2+b的顶点坐标为(0,﹣1),且经过点A(﹣2,0).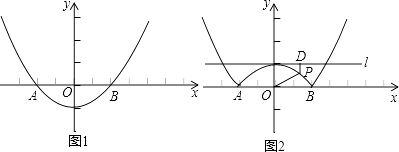 (1)、求抛物线的解析式;(2)、若将抛物线y=ax2+b中在x轴下方的图象沿x轴翻折到x轴上方,x轴上方的图象保持不变,就得到了函数y=|ax2+b|图象上的任意一点P,直线l是经过(0,1)且平行与x轴的直线,过点P作直线l的垂线,垂足为D,猜想并探究:PO与PD的差是否为定值?如果是,请求出此定值;如果不是,请说明理由.
(1)、求抛物线的解析式;(2)、若将抛物线y=ax2+b中在x轴下方的图象沿x轴翻折到x轴上方,x轴上方的图象保持不变,就得到了函数y=|ax2+b|图象上的任意一点P,直线l是经过(0,1)且平行与x轴的直线,过点P作直线l的垂线,垂足为D,猜想并探究:PO与PD的差是否为定值?如果是,请求出此定值;如果不是,请说明理由.(注:在解题过程中,如果你觉得有困难,可以阅读下面的材料)
附阅读材料:
① 在平面直角坐标系中,若A、B两点的坐标分别为A(x1 , y1),B(x2 , y2),则A,B两点间的距离为|AB|= ,这个公式叫两点间距离公式.
例如:已知A,B两点的坐标分别为(﹣1,2),(2,﹣2),则A,B两点间的距离为|AB|= =5.
② 因式分解:x4+2x2y2+y4=(x2+y2)2 .