传统文化-【培优周周练】浙教版数学八年级上册-在线组卷题库

1. 如图①，油纸伞是中国传统工艺品之一，起源于中国的一种纸制或布制伞．油纸伞的制作工艺十分巧妙，如图②，伞圈D沿着伞柄 $A P$ 滑动时，伞柄 $A P$ 始终平分同一平面内两条伞骨所成的 $∠ B A C$ ，伞骨 $B D$ ， $C D$ 的B ， C点固定不动，且到点A的距离 $A B = A C$ ．

(1)、当D点在伞柄 $A P$ 上滑动时，处于同一平面的两条伞骨 $B D$ 和 $C D$ 相等吗？请说明理由．

(2)、如图③，当油纸伞撑开时，伞的边缘M ， N与点D在同一直线上，若 $∠ B A C = 140 °$ ， $∠ M B D = 120 °$ ，求 $∠ C D A$ 的度数．

查看试题解析
2. 山西皮影戏又称“影戏”或“影子戏”，属于传统民间艺术，皮影是一种以兽皮或纸板做成的人物剪影，在制作人物剪影中，给出下面4个条件：① $A B = A C$ ；② $A D = A E$ ；③ $∠ A B D = ∠ A C E$ ；④ $∠ B A E = ∠ C A D$ .

(1)、在上述四个条件中，选三个条件作为题设，另一个作为结论，其中真命题有哪几个？（用序号表示即可）

(2)、请选择（1）中的一个命题证明其符合题意性.

查看试题解析

3. 我国传统建筑中，窗框(如图1)的图案玲珑剔透、千变万化．窗框一部分如图2所示，它是一个轴对称图形，其对称轴有（）

A、1条 B、2条 C、3条 D、4条

查看试题解析

4. 我国古代《易经》记载，远古时期人们通过在绳子上打结来记录数量，即“结绳记数”．如图，一位妇女在从右到左依次排列的绳子上打结，满五进一，用来记录采集到野果的个数．若她采集到的一筐野果不少于46个则在第2根绳子上的打结数至少是（）

A、2 B、3 C、4 D、5

查看试题解析
5. 综合与实践问题情境：“文房四宝”是中国独有的书法绘画工具，即笔、墨、纸、砚，文房四宝之名，起源于南北朝时期．某中学为了落实双减政策，丰富学生的课后服务活动，开设了书法社团，计划为学生购买A，B两种型号“文房四宝”共40套．已知某文化用品店每套A型号的“文房四宝”的标价比B型号的“文房四宝”的标价高30%，若按标价购买需花费4300元，其中购买B型号“文房四宝”花费3000元．
问题解决：

(1)、求每套B型号的“文房四宝”的标价．

(2)、若经过与店主协商，考虑到购买较多，店主同意该中学按A型号“文房四宝”九折，B型号“文房四宝”八折的优惠价购入，则购买原定数量的A，B型号“文房四宝”共需花费多少元？

(3)、一段时间后，由于传统文化广受关注，另一所学校想要购入A，B两种型号“文房四宝”共100套。店主继续以（2）中的折扣价进行销售，已知A，B两种型号的“文房四宝”每套进价分别为67元和50元，若通过此单生意，该店主获利不低于3800元，则该校在这家店至少买了套A型“文房四宝”？

查看试题解析

6. “漏刻”是我国古代一种利用水流计时的工具（如图①），综合实践小组用甲、乙两个透明的竖直放置的容器和一根装有节流阀（控制水的流速）的软管，制作了类似“漏刻”的简易计时装置（如图②）.上午10：00，综合实践小组在甲容器里加满水，经过实验得到甲容器的水面高度h(cm)与流水时间t(min)的关系如图③所示，下列说法错误的是（）

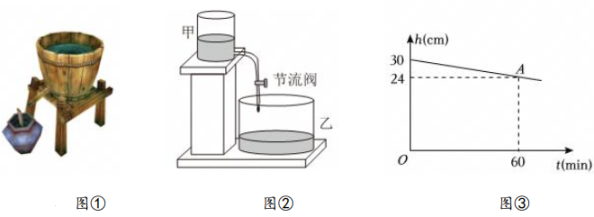A、甲容器的初始水面高度为30cm B、15：00甲容器的水流光 C、甲容器的水面高度h与流水时间t的关系式为 $h = - 0.1 t + 30$ D、12：00时甲容器的水面高度为12cm

查看试题解析
7. 综合与实践
【问题背景】杆秤是我国古代传统的度量衡三大件之一，在学习了杆秤相关知识之后，小红学习小组想利用一根木棒制作一个简易杆秤．
【制作实验】
（1）如图所示，在木棒上先确定点 $O$ 为杆秤提组，点A处挂托盘，选取的托盘质量 $m_{0} = 0.5 kg$ ，秤砣质量 $m_{2} = 1 kg$ ，测得 $l_{1} = O A = 3 cm$ ．
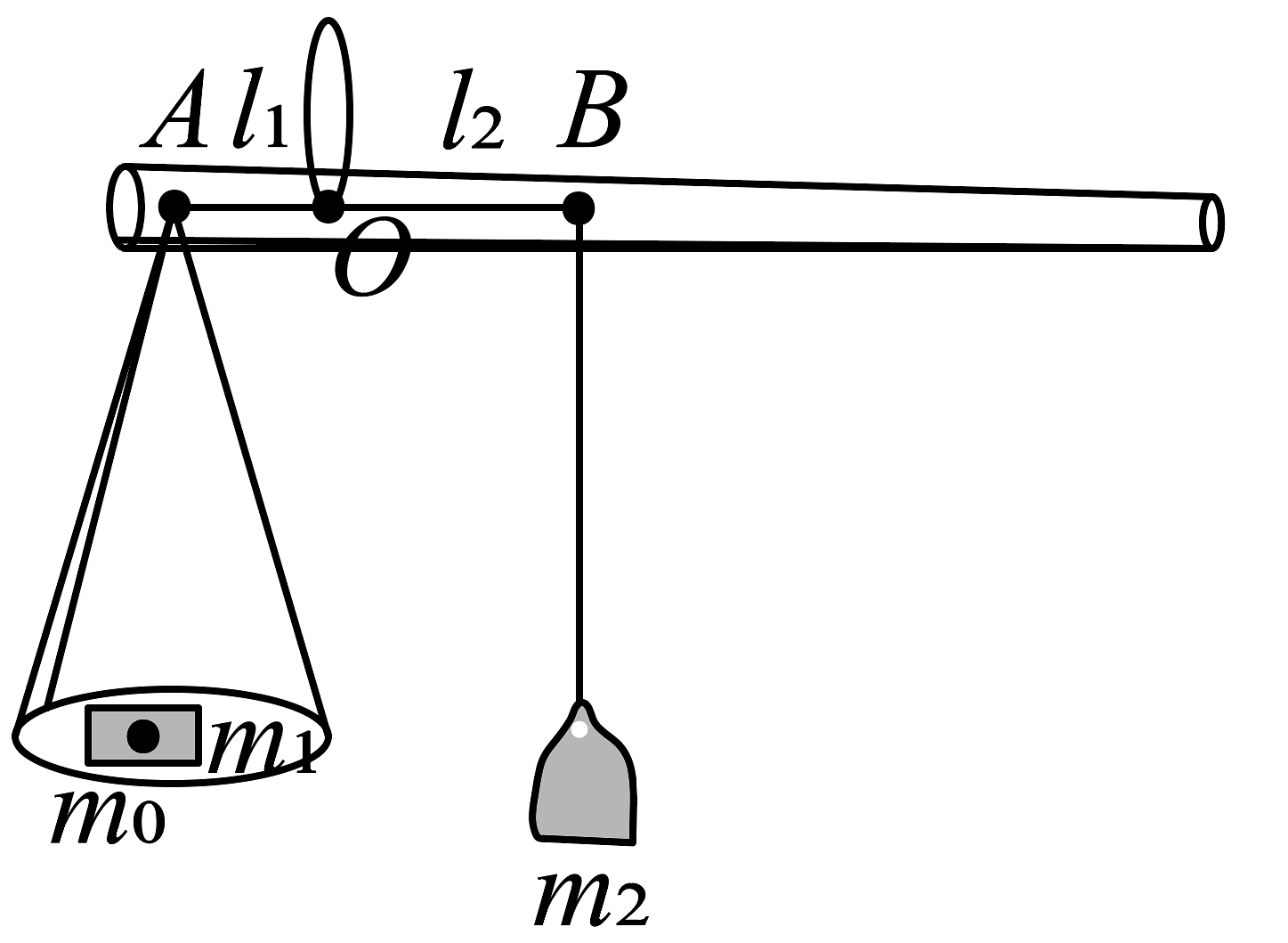
（2）先在托盘里加相应质量的物体，调整秤砣位置，使杆秤保持平衡，记录 $O B$ 的长度，获得的实验数据如表所示：
物体质量 $m_{1} / kg$
0
1
2
3
4
$O B$ 长度 $l_{2} / cm$
1.5
4.5
7.5
10.5
13.5
任务1：杆秤在不挂重物而保持平衡时，其点 $B$ 所处的位置，称为定盘星．由表可知，定盘星和提纽的距离是 ▲ ．
【建立模型】
任务2：小组讨论认为 $O B$ 长度 $l_{2}$ 与物体质量 $m_{1}$ 的关系可以用一次函数来刻画．请求出 $O B$ 长度 $l_{2}$ 与物体质量 $m_{1}$ 的函数关系式．
【结论应用】
任务3：经测量，发现该木棒在提纽 $O$ 挂秤砣一侧的长度为 $34 cm$ ，根据要求，制作杆秤刻度时需在杆头和杆尾各预留 $2.5 cm$ 长的部分用作杆秤美化，求该杆秤称量重物的最大量程．

查看试题解析
8. 缂丝，是中国传统丝绸艺术品中的精华．缂丝织造技艺主要是使用古老的木机（如图①）及若干竹制的梭子和拨子，经过“通经断纬”的织造方法，将五彩的蚕丝线缂织成一幅色彩丰富的织物．缂丝工匠现要完成一件织品，工作一段时间后，记录了工作时间和织品长度的数据变化，并从函数角度进行了如下实验探究．
图①
【数据观察】记录的工作时间x（时）和织品长度y（厘米）的数据变化，如下表：
工作时间x（时）
0
2
4
6
8
织品长度y（厘米）
3
3.6
4.2
4.8
5.4
【探索发现】

(1)、建立平面直角坐标系，如图②，横轴表示记录的工作时间x ，纵轴表示织品长度y ，描出以表格中数据为坐标的各点．
图②

(2)、观察上述各点的分布规律，判断它们是否在同一条直线上，如果在同一条直线上，求出这条直线所对应的函数表达式，如果不在同一条直线上，说明理由．

(3)、如果每天工作10小时，要完成长为240厘米的织品，共需要多少天？

查看试题解析
9. 综合与实践
某班同学分三个小组进行“板凳中的数学”的项目式学习研究．第一小组负责调查板凳的历史及结构特点；第二小组负责研究板凳中蕴含的数学知识；第三小组负责汇报和交流．下面是第三小组汇报的部分内容，请你阅读相关信息，并解答“建立模型”中的问题．
【背景调查】
图①中的板凳又叫“四脚八叉凳”，是中国传统家具，其榫卯结构体现了古人含蓄内敛的审美观．榫眼的设计很有讲究，木工一般用铅笔画出凳面的对称轴，以对称轴为基准向两边各取相同的长度，确定榫眼的位置，如图②所示．板凳的结构设计体现了数学的对称美．
【收集数据】
小组收集了一些板凳并进行了测量．设以对称轴为基准向两边各取相同的长度为x mm ，凳面的宽度为y mm ，记录如下：
以对称轴为基准向两边各取相同的长度x/mm
16.5
19.8
23.1
26.4
29.7
凳面的宽度y/mm
115.5
132
148.5
165
181.5
【分析数据】
如图③，小组根据表中x ， y的数值，在平面直角坐标系中描出了各点．
【建立模型】
请你帮助小组解决下列问题：

(1)、观察上述各点的分布规律，它们是否在同一条直线上？如果在同一条直线上，求出这条直线所对应的函数解析式；如果不在同一条直线上，说明理由．

(2)、当凳面宽度为213mm时，以对称轴为基准向两边各取相同的长度是多少？

查看试题解析
10. 综合与实践：
【问题背景】沙漏又称“沙钟”，是我国古代一种计量时间的仪器，它是根据流沙从一个容器漏到另一个容器的数量来计量时间 $.$ 综合实践小组在进行项目化学习时，根据古代的沙漏模型 $($ 图 $1)$ 制作了一套“沙漏计时装置”，该装置由沙漏和精密电子秤组成，电子秤上放置盛沙容器 $.$ 沙子缓慢匀速地从沙漏孔漏到精密电子称上的容器内，可以通过读取电子秤的读数计算时间 $($ 假设沙子足够 $)$ ．
【实验操作】该实验小组从函数角度进行了如下实验探究：
实验观察：实验小组通过观察，每两小时记录一次电子秤读数，得到如表：
沉淀时间 $x (h)$
$0$
$2$
$4$
$6$
$8$
电子秤读数 $y ($ 克 $)$
$6$
$18$
$30$
$42$
$54$

(1)、问题 $1$ ：建立平面直角坐标系，如图 $2$ ，横轴表示漏沙时间 $x$ ，纵坐标表示精密电子称的读数 $y$ ，描出以表中的数据为坐标的各点；

(2)、【建立模型】问题 $2$ ：观察上述各点的分布规律，依次将各点连接起来，判断它们是否在同一条直线上，如果在同一条直线上，请你建立适当的函数模型，并求出函数表达式：如果不在同一条直线上 $.$ 请说明理由；

(3)、【结论应用】问题 $3$ ：应用上述发现的规律估算：
①若漏沙时间为 $9$ 小时，精密电子称的读数为多少？
②若本次实验开始记录的时间是上午 $7$ ： $30$ ，当精密电子秤的读数为 $72$ 克时是几点钟？ $($ 时间为 $24$ 时制 $)$

查看试题解析

传统文化-【培优周周练】浙教版数学八年级上册

一、第一章三角形的初步知识

二、第二章特殊三角形

三、第三章一元一次不等式

四、第四章图形与坐标

五、第五章一次函数

物体质量 $m_{1} / kg$	0	1	2	3	4
$O B$ 长度 $l_{2} / cm$	1.5	4.5	7.5	10.5	13.5

工作时间x（时）	0	2	4	6	8
织品长度y（厘米）	3	3.6	4.2	4.8	5.4

以对称轴为基准向两边各取相同的长度x/mm	16.5	19.8	23.1	26.4	29.7
凳面的宽度y/mm	115.5	132	148.5	165	181.5

沉淀时间 $x (h)$	$0$	$2$	$4$	$6$	$8$
电子秤读数 $y ($ 克 $)$	$6$	$18$	$30$	$42$	$54$

传统文化-【培优周周练】浙教版数学八年级上册

一、第一章 三角形的初步知识

二、第二章 特殊三角形

三、第三章 一元一次不等式

四、第四章 图形与坐标

五、第五章 一次函数

一、第一章三角形的初步知识

二、第二章特殊三角形

三、第三章一元一次不等式

四、第四章图形与坐标

五、第五章一次函数