勾股定理的常见模型-【培优周周练】浙教版数学八年级上册
试卷更新日期:2025-08-06 类型:复习试卷
一、“勾股树”模型
-
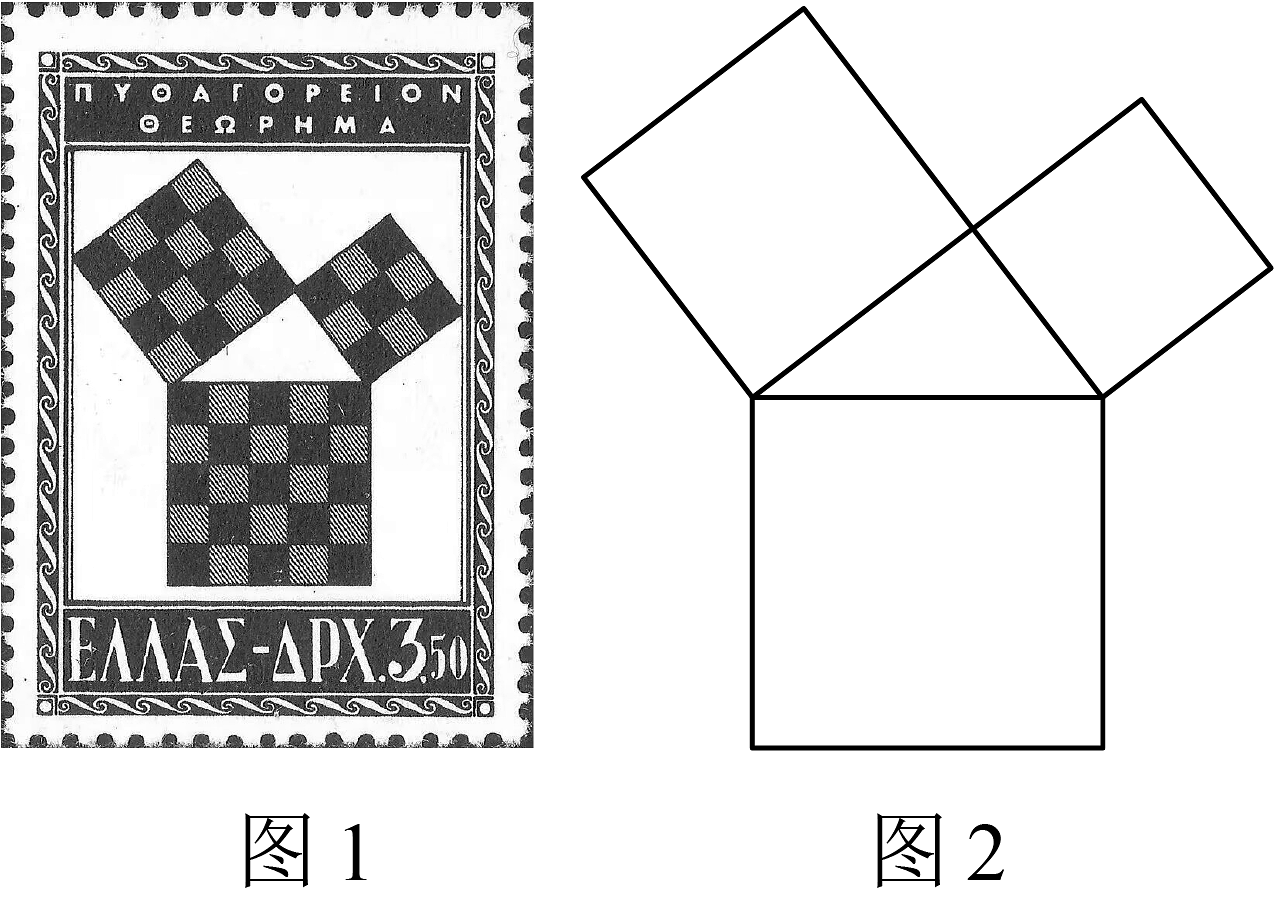
1. 1995年,希腊为纪念毕达哥拉斯学派发行了如图1所示的邮票,图片中间是三个正方形顶点相连构成一个三角形.如图2,若中间的三角形为直角三角形,则三个正方形的面积可以是( )
 A、2,3,5 B、3,4,5 C、6,8,13 D、5,12,142. 有一个边长为1的大正方形,经过1次“生长”后,在它的左右肩上生出两个小正方形,其中三个正方形围成的三角形是直角三角形,再经过1次“生长”后,形成的图形如图1所示.如果继续“生长”下去,它将变得“枝繁叶茂”,若“生长”了2024次后形成的图形如图2所示,则图2中所有的正方形的面积和是( )
A、2,3,5 B、3,4,5 C、6,8,13 D、5,12,142. 有一个边长为1的大正方形,经过1次“生长”后,在它的左右肩上生出两个小正方形,其中三个正方形围成的三角形是直角三角形,再经过1次“生长”后,形成的图形如图1所示.如果继续“生长”下去,它将变得“枝繁叶茂”,若“生长”了2024次后形成的图形如图2所示,则图2中所有的正方形的面积和是( )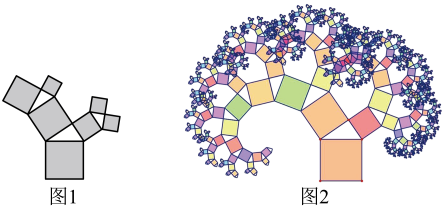 A、2025 B、2024 C、 D、3. 如图 , , , , 以这个直角三角形两直角边为边作正方形图由图的两个小正方形向外分别作直角边之比为:的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形, , 按此规律,则图中所有正方形的面积和为( )
A、2025 B、2024 C、 D、3. 如图 , , , , 以这个直角三角形两直角边为边作正方形图由图的两个小正方形向外分别作直角边之比为:的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形, , 按此规律,则图中所有正方形的面积和为( ) A、 B、 C、 D、4. 如图, 以 Rt 的三边为直角边分别向外作等腰直角三角形. 若 , 则图中阴影部分的面积为
A、 B、 C、 D、4. 如图, 以 Rt 的三边为直角边分别向外作等腰直角三角形. 若 , 则图中阴影部分的面积为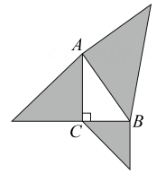 5. 勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
5. 勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
 (1)、①如图2,3,4,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,面积分别为 , , , 利用勾股定理,判断这3个图形中面积关系满足的有________个.
(1)、①如图2,3,4,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,面积分别为 , , , 利用勾股定理,判断这3个图形中面积关系满足的有________个.②如图5,分别以直角三角形三边为直径作半圆,设图中两个月牙形图案(图中阴影部分)的面积分别为 , , 直角三角形面积为 , 也满足吗?若满足,请证明;若不满足,请求出 , , 的数量关系.
(2)、如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图6所示的“勾股树”.在如图7所示的“勾股树”的某部分图形中,设大正方形M的边长为定值m,四个小正方形A,B,C,D的边长分别为a,b,c,d,则__________.二、“赵爽弦图”模型
-
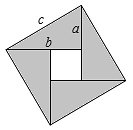
6. 如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“勾股圆方图”(又称赵爽弦图),它是由四个全等的直角三角形(直角边分别为a,b,斜边为c)与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积为11,小正方形的面积为3,则的值为( )
 A、68 B、89 C、119 D、1307. 如图,四个全等的直角三角形与中间的小正方形EFGH拼成了一个大正方形ABCD , 连结AC , 交BE于点 , 若正方形ABCD的面积为.则的值是( )
A、68 B、89 C、119 D、1307. 如图,四个全等的直角三角形与中间的小正方形EFGH拼成了一个大正方形ABCD , 连结AC , 交BE于点 , 若正方形ABCD的面积为.则的值是( ) A、5.5 B、6.5 C、7 D、7.58. 如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD 与正方形EFGH,连接 EG,BD 相交于点O,BD 与HC相交于点 P.若GO=GP,则 的值是( ).
A、5.5 B、6.5 C、7 D、7.58. 如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD 与正方形EFGH,连接 EG,BD 相交于点O,BD 与HC相交于点 P.若GO=GP,则 的值是( ).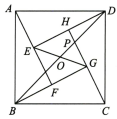 A、 B、 C、 D、9. 在认识了勾股定理的赵爽弦图后,一位同学尝试将个全等的小正方形嵌入长方形内部,其中点 , , , 分别在长方形的边 , , 和上,若 , , 则小正方形的边长为( )
A、 B、 C、 D、9. 在认识了勾股定理的赵爽弦图后,一位同学尝试将个全等的小正方形嵌入长方形内部,其中点 , , , 分别在长方形的边 , , 和上,若 , , 则小正方形的边长为( ) A、 B、 C、 D、10. 如图是我国古代著名的赵爽弦图的示意图,其由四个全等的直角三角形拼接成一个正方形 , 其中 , , 则的值是 .
A、 B、 C、 D、10. 如图是我国古代著名的赵爽弦图的示意图,其由四个全等的直角三角形拼接成一个正方形 , 其中 , , 则的值是 . 11. 图1是由5个全等的直角三角形与一个小正方形组成,延长交、分别于点、 , 延长交于点(如图2).
11. 图1是由5个全等的直角三角形与一个小正方形组成,延长交、分别于点、 , 延长交于点(如图2).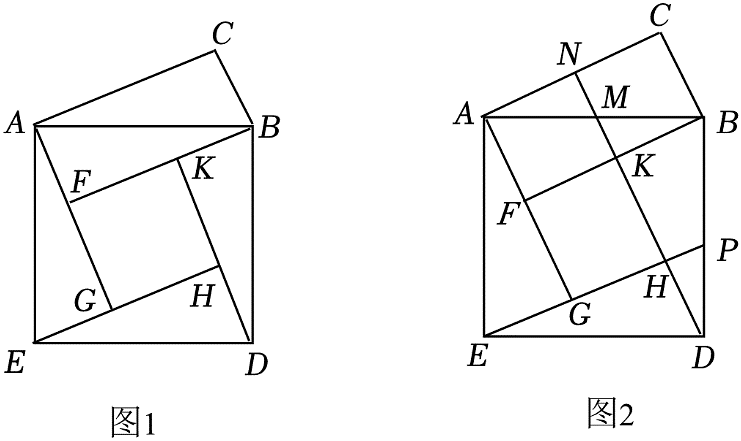
(1)若的面积为 , 小正方形的面积为 , 则=;
(2)如图2,若 , 则=(用含的代数式表示).
12. 勾股定理的证明方法多种多样,我国古代数学家赵爽构造“弦图”证明了勾股定理,后人称其为“赵爽弦图”.“赵爽弦图”是由四个全等的直角三角形拼成.如图1为赵爽弦图,其中∠AGB=∠DFA=∠CED=∠BHC=90°,连结AE交BG于点P,连结BE,得到图2,若∠ABE=∠AEB. (1)、求证:EF=DF;(2)、若EF=2,求PE的长.
(1)、求证:EF=DF;(2)、若EF=2,求PE的长.三、蚂蚁爬行模型
-
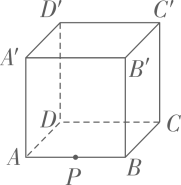
13. 如图,在棱长为2 的正方体中,蚂蚁从正方体下方一边 AB 的中点 P 出发爬到顶点( 处,若蚂蚁选择的路径是最短的,则最短路径长为.
 14. 如图,长方体盒子的长、宽、高分别为2,2,4,若一只蚂蚁想从盒底的点 A 处沿盒子的表面爬行一周到达点 B处,则蚂蚁爬行的最短路径长为.
14. 如图,长方体盒子的长、宽、高分别为2,2,4,若一只蚂蚁想从盒底的点 A 处沿盒子的表面爬行一周到达点 B处,则蚂蚁爬行的最短路径长为.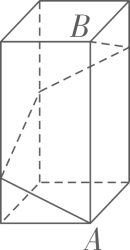 15. 如图,有一个高为8cm ,底面周长为6 cm的圆柱形容器,在外壁距下沿3c m的点A处有一只蚂蚁,与蚂蚁相对的内壁距上沿4 cm 的点 B 处有一滴蜂蜜,则蚂蚁从A 处到蜂蜜 B 处所走的最短路径长为.
15. 如图,有一个高为8cm ,底面周长为6 cm的圆柱形容器,在外壁距下沿3c m的点A处有一只蚂蚁,与蚂蚁相对的内壁距上沿4 cm 的点 B 处有一滴蜂蜜,则蚂蚁从A 处到蜂蜜 B 处所走的最短路径长为. 16. 如图,已知圆锥的母线长为6,底面圆的半径为3,在圆锥的底面边缘上点A处有一只蚂蚁,想吃到与点A 相对的母线的中点B处的食物,这只蚂蚁从点 A 出发,沿着曲面爬到点 B,则最短路线长是.
16. 如图,已知圆锥的母线长为6,底面圆的半径为3,在圆锥的底面边缘上点A处有一只蚂蚁,想吃到与点A 相对的母线的中点B处的食物,这只蚂蚁从点 A 出发,沿着曲面爬到点 B,则最短路线长是.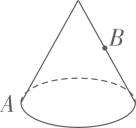 17. 如图,是一个四级台阶,它的每一级的长、宽和高分别为5,1.5 和1.5,A 和 B 是这个台阶的两个相对的端点,B点上有一只蚂蚁,想到A点去觅食,则蚂蚁从 B 点出发,沿着台阶面爬到A点,最短路径长为.
17. 如图,是一个四级台阶,它的每一级的长、宽和高分别为5,1.5 和1.5,A 和 B 是这个台阶的两个相对的端点,B点上有一只蚂蚁,想到A点去觅食,则蚂蚁从 B 点出发,沿着台阶面爬到A点,最短路径长为. 18. 问题情境:如图①,一只蚂蚁在一个长为 , 宽为的长方形地毯上爬行,地毯上堆放着一根正三棱柱的木块,它的侧棱平行且等于宽 , 木块从正面看是一个边长为的等边三角形,求一只蚂蚁从点处到达点处需要走的最短路程.
18. 问题情境:如图①,一只蚂蚁在一个长为 , 宽为的长方形地毯上爬行,地毯上堆放着一根正三棱柱的木块,它的侧棱平行且等于宽 , 木块从正面看是一个边长为的等边三角形,求一只蚂蚁从点处到达点处需要走的最短路程.数学抽象:将蚂蚁爬行过的木块的侧面“拉直”“铺平”,“化曲为直”,连接 .
 (1)、线段的长即蚂蚁从点处到达点处需要走的最短路程,依据是;(2)、问题解决:求出这只蚂蚁从点处到达点处需要走的最短路程.19. “转化”是一种重要的数学思想,将空间问题转化为平面问题是转化思想的一个重要方面.例如,如图①,一个立方体的棱长为1,有一只蚂蚁从点出发,沿着立方体的表面爬行到点.沿怎样的路线爬行路程最短?要解决这个问题,我们可以把立方体展开(如图②③,把空间两个面上的两点A,G之间的最短路径问题转化为同一个面上两点之间的距离问题.根据“两点之间线段最短”,可知蚂蚁沿线段AG爬行路径最短,最短路径长为.
(1)、线段的长即蚂蚁从点处到达点处需要走的最短路程,依据是;(2)、问题解决:求出这只蚂蚁从点处到达点处需要走的最短路程.19. “转化”是一种重要的数学思想,将空间问题转化为平面问题是转化思想的一个重要方面.例如,如图①,一个立方体的棱长为1,有一只蚂蚁从点出发,沿着立方体的表面爬行到点.沿怎样的路线爬行路程最短?要解决这个问题,我们可以把立方体展开(如图②③,把空间两个面上的两点A,G之间的最短路径问题转化为同一个面上两点之间的距离问题.根据“两点之间线段最短”,可知蚂蚁沿线段AG爬行路径最短,最短路径长为.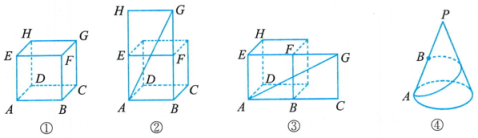
下面请你思考蚂蚁在圆锥表面的爬行问题:如图④,圆锥的底面半径为1,母线长为4.一只蚂蚁从圆锥底面圆周上一点出发,沿着圆锥的侧面爬过一圈到达母线PA的中点.问:蚂蚁爬行的最短路径长是多少?
四、矩形翻折形成的全等模型
-
20. 如图,矩形沿着直线折叠,使点C落在点处, , , 则的长度为( )
 A、4 B、6 C、8 D、1021. 如图,折叠长方形纸片 , 使得点D落在边上的点F处,折痕为 , 已知 , , 则的长为( )
A、4 B、6 C、8 D、1021. 如图,折叠长方形纸片 , 使得点D落在边上的点F处,折痕为 , 已知 , , 则的长为( ) A、3 B、 C、 D、22. 如图,在矩形纸片中, , , 折叠纸片使边落在对角线上,折痕为 , 则的面积为( )
A、3 B、 C、 D、22. 如图,在矩形纸片中, , , 折叠纸片使边落在对角线上,折痕为 , 则的面积为( )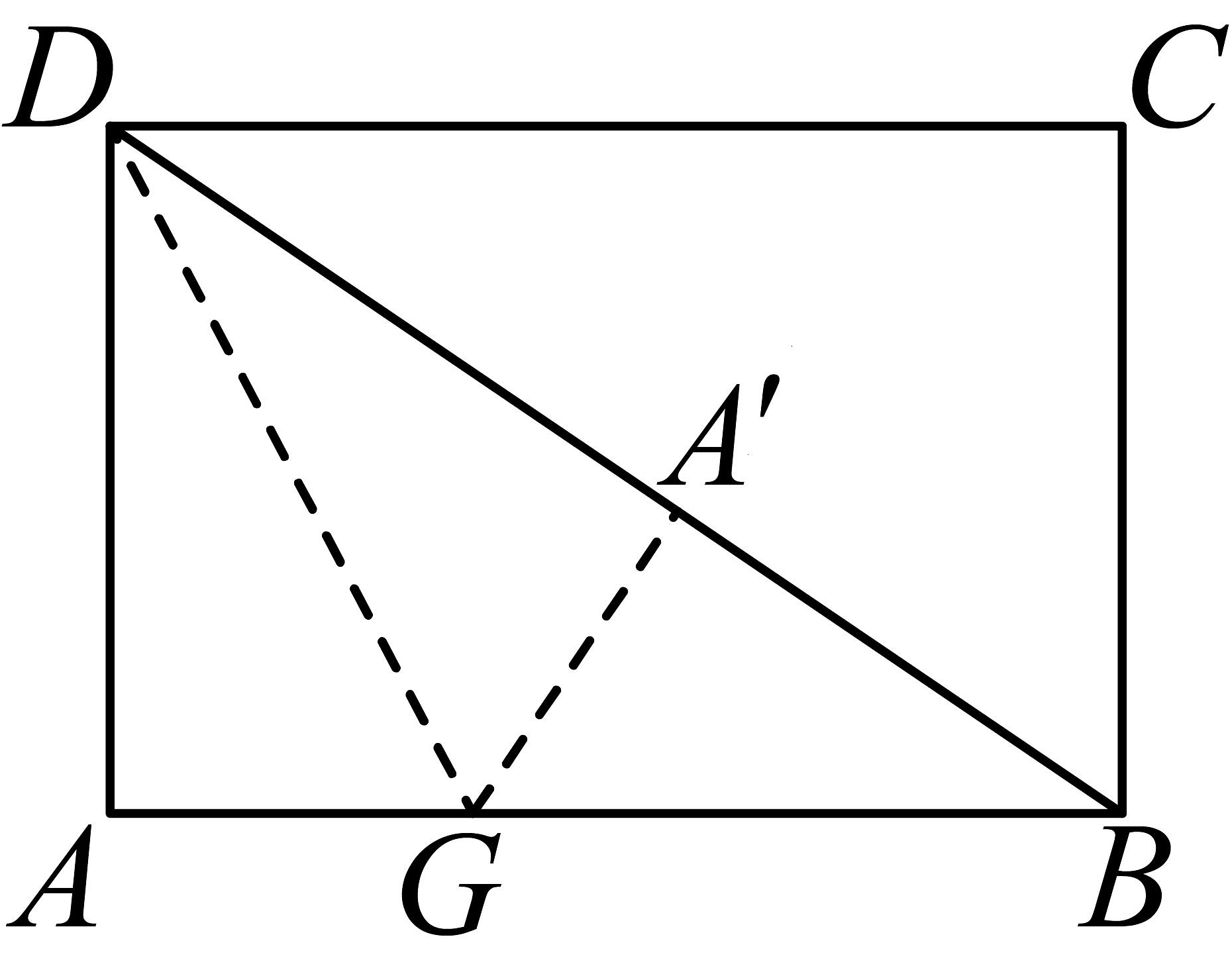 A、 B、 C、 D、23. 如图,在矩形中, , . 点O为矩形的对称中心,点E为边上的动点,连接并延长交于点F.将四边形沿着翻折,得到四边形 , 边交边于点G,连接 , 则的面积的最小值为( )
A、 B、 C、 D、23. 如图,在矩形中, , . 点O为矩形的对称中心,点E为边上的动点,连接并延长交于点F.将四边形沿着翻折,得到四边形 , 边交边于点G,连接 , 则的面积的最小值为( ) A、18-3 B、 C、 D、24. 在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:第一步 : 将矩形纸片利用图 1 的方法折出一个正方形 , 然后把纸片展平.第二步: 将图 1 中的矩形纸片折叠, 使点 恰好落在点 处, 得到折痕 , 如图 2 .根据以上的操作, 若 , 则线段 的长是( )
A、18-3 B、 C、 D、24. 在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:第一步 : 将矩形纸片利用图 1 的方法折出一个正方形 , 然后把纸片展平.第二步: 将图 1 中的矩形纸片折叠, 使点 恰好落在点 处, 得到折痕 , 如图 2 .根据以上的操作, 若 , 则线段 的长是( )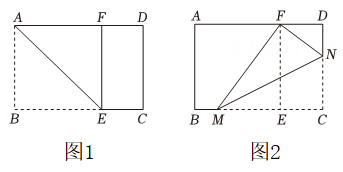 A、3 B、 C、2 D、125. 小明同学手中有一张矩形纸片ABCD , AD=12cm , CD=10cm , 他进行了如下操作:
A、3 B、 C、2 D、125. 小明同学手中有一张矩形纸片ABCD , AD=12cm , CD=10cm , 他进行了如下操作:第一步,如图①,将矩形纸片对折,使AD与BC重合,得到折痕MN , 将纸片展平.
第二步,如图②,再一次折叠纸片,把△ADN沿AN折叠得到△AD'N , AD'交折痕MN于点E , 则线段EN的长为( )
 A、8cm B、 C、 D、
A、8cm B、 C、 D、

