广东省广州市2025年中考数学真题
试卷更新日期:2025-08-01 类型:中考真卷
一、单选题
-
1. 下列四个选项中,负无理数的是( )A、 B、 C、0 D、32. 如图,将绕直角边所在直线旋转一周,可以得到的立体图形是( )
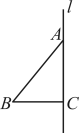 A、
A、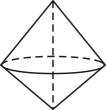 B、
B、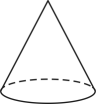 C、
C、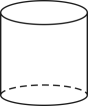 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 关于x的方程根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、只有一个实数根5. 某地一周的每天最高气温如下表,利用这些数据绘制了下列四个统计图,最适合描述气温变化趋势的是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 关于x的方程根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、只有一个实数根5. 某地一周的每天最高气温如下表,利用这些数据绘制了下列四个统计图,最适合描述气温变化趋势的是( )星期
一
二
三
四
五
六
日
最高气温/℃
25
25
28
30
33
30
29
A、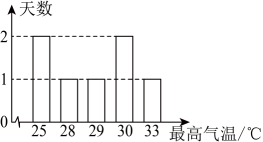 B、
B、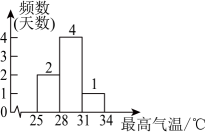 C、
C、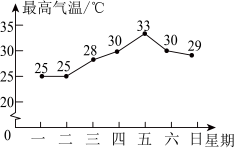 D、
D、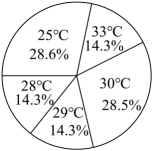 6. 如图,在平面直角坐标系中,点 , 点 , 若将直线向上平移d个单位长度后与线段有交点,则d的取值范围是( )
6. 如图,在平面直角坐标系中,点 , 点 , 若将直线向上平移d个单位长度后与线段有交点,则d的取值范围是( )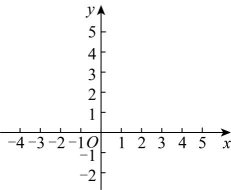 A、 B、 C、 D、7. 若 , 反比例函数的图象在( )A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限8. 如图,菱形的面积为10,点E , F , G , H分别为 , , , 的中点,则四边形的面积为( )
A、 B、 C、 D、7. 若 , 反比例函数的图象在( )A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限8. 如图,菱形的面积为10,点E , F , G , H分别为 , , , 的中点,则四边形的面积为( )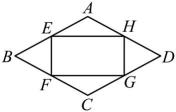 A、 B、5 C、4 D、89. 如图,的直径 , C为中点,点D在弧上, , 点P是上的一个动点,则周长的最小值是( )
A、 B、5 C、4 D、89. 如图,的直径 , C为中点,点D在弧上, , 点P是上的一个动点,则周长的最小值是( )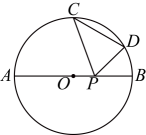 A、 B、 C、 D、10. 在平面直角坐标系中,两点 , 在抛物线 , 则下列结论中正确的是( )A、当且时,则 B、当时,则 C、当且时,则 D、当时,则
A、 B、 C、 D、10. 在平面直角坐标系中,两点 , 在抛物线 , 则下列结论中正确的是( )A、当且时,则 B、当时,则 C、当且时,则 D、当时,则二、填空题
-
11. 如图,直线 , 相交于点O . 若 , 则的度数为 .
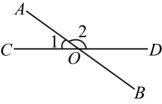 12. 如图,在中,点 , 分别在 , 上, , 若 , 则 .
12. 如图,在中,点 , 分别在 , 上, , 若 , 则 .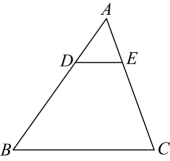 13. 要使代数式有意义,则x的取值范围是 .14. 如图,在中, , 平分 , 已知 , , 则点B到的距离为 .
13. 要使代数式有意义,则x的取值范围是 .14. 如图,在中, , 平分 , 已知 , , 则点B到的距离为 . 15. 若抛物线的顶点在直线上,则m的值为 .16. 已知的半径为 , 所在平面内有一动点 , 过点可以引的两条切线 , , 切点分别为 , . 点与圆心的距离为 , 则的取值范围是;若过点作交直线于点(点不与点重合),线段与交于点 . 设 , , 则关于的函数解析式为 .
15. 若抛物线的顶点在直线上,则m的值为 .16. 已知的半径为 , 所在平面内有一动点 , 过点可以引的两条切线 , , 切点分别为 , . 点与圆心的距离为 , 则的取值范围是;若过点作交直线于点(点不与点重合),线段与交于点 . 设 , , 则关于的函数解析式为 .三、解答题
-
17. 解不等式组 , 并在数轴上表示解集.18. 如图, , , . 求证: .
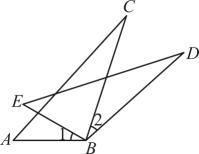 19. 求代数式的值,其中 .20. 为了弘扬中华优秀传统文化,某校开展主题为“多彩非遗,国韵传扬”的演讲比赛.评委从演讲的内容、能力、效果三个方面为选手打分,各项成绩均按百分制计.进入决赛的前两名选手需要确定名次(不能并列),他们的单项成绩如下表所示:
19. 求代数式的值,其中 .20. 为了弘扬中华优秀传统文化,某校开展主题为“多彩非遗,国韵传扬”的演讲比赛.评委从演讲的内容、能力、效果三个方面为选手打分,各项成绩均按百分制计.进入决赛的前两名选手需要确定名次(不能并列),他们的单项成绩如下表所示:选手
内容
能力
效果
甲
乙
(1)、分别计算甲、乙两名选手的平均成绩(百分制),能否以此确定两人的名次?(2)、如果评委认为“内容”这一项最重要,内容、能力、效果的成绩按照的比确定,以此计算两名选手的平均成绩(百分制),并确定两人的名次;(3)、如果你是评委,请按你认为各项的“重要程度”设计三项成绩的比,并解释设计的理由.21. 如图,曲线过点 .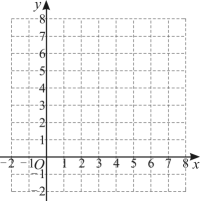 (1)、求t的值;(2)、直线也经过点P , 求l与y轴交点的坐标,并在图中画出直线l;(3)、在(2)的条件下,若在l与两坐标轴围成的三角形内部(不包含边界)随机取一个格点(横、纵坐标都是整数的点),求该格点在曲线G上的概率.22. 智能机器人广泛应用于智慧农业.为了降低成本和提高采摘效率,某果园引进一台智能采摘机器人进行某种水果采摘.(1)、若用人工采摘的成本为a元,相比人工采摘,用智能机器人采摘的成本可降低 . 求用智能机器人采换的成本是多少元;(用含a的代数式表示)(2)、若要采摘4000千克该种水果,用这台智能采摘机器人采摘比4个工人同时采摘所需的天数还少1天,已知这台智能采摘机器人采摘的效率是一个工人的5倍,求这台智能采摘机器人每天可采摘该种水果多少千克.23. 宽与长的比是(约为)的矩形叫做黄金矩形.现有一张黄金矩形纸片 , 长 . 如图1,折叠纸片 , 点B落在上的点E处,折痕为 , 连接 , 然后将纸片展开.
(1)、求t的值;(2)、直线也经过点P , 求l与y轴交点的坐标,并在图中画出直线l;(3)、在(2)的条件下,若在l与两坐标轴围成的三角形内部(不包含边界)随机取一个格点(横、纵坐标都是整数的点),求该格点在曲线G上的概率.22. 智能机器人广泛应用于智慧农业.为了降低成本和提高采摘效率,某果园引进一台智能采摘机器人进行某种水果采摘.(1)、若用人工采摘的成本为a元,相比人工采摘,用智能机器人采摘的成本可降低 . 求用智能机器人采换的成本是多少元;(用含a的代数式表示)(2)、若要采摘4000千克该种水果,用这台智能采摘机器人采摘比4个工人同时采摘所需的天数还少1天,已知这台智能采摘机器人采摘的效率是一个工人的5倍,求这台智能采摘机器人每天可采摘该种水果多少千克.23. 宽与长的比是(约为)的矩形叫做黄金矩形.现有一张黄金矩形纸片 , 长 . 如图1,折叠纸片 , 点B落在上的点E处,折痕为 , 连接 , 然后将纸片展开.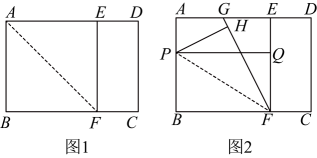 (1)、求的长;(2)、求证:四边形是黄金矩形;(3)、如图2,点G为的中点,连接 , 折叠纸片 , 点B落在上的点H处,折痕为 , 过点P作于点Q . 四边形是否为黄金矩形?如果是,请证明:如果不是,请说明理由.24. 某玩转数学小组发现隧道前通常设有涉水线和限高架等安全警示,为探究其内在的数学原理,该小组考察了如图1所示的双向通行隧道.以下为该小组研究报告的部分记录,请认真阅读,解决问题.
(1)、求的长;(2)、求证:四边形是黄金矩形;(3)、如图2,点G为的中点,连接 , 折叠纸片 , 点B落在上的点H处,折痕为 , 过点P作于点Q . 四边形是否为黄金矩形?如果是,请证明:如果不是,请说明理由.24. 某玩转数学小组发现隧道前通常设有涉水线和限高架等安全警示,为探究其内在的数学原理,该小组考察了如图1所示的双向通行隧道.以下为该小组研究报告的部分记录,请认真阅读,解决问题.
发现问题确定目标
涉水线设置
限高架设置
数学抽象绘制图形
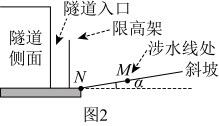
隧道及斜坡的侧面示意图,可近似如图2所示.
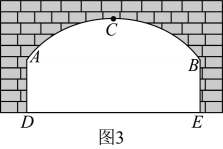
图3为隧道横截面示意图,由抛物线的一部分和矩形的三边构成.
信息收集资料整理
当隧道内积水的水深为0.27米时,(即积水达到涉水线处),车辆应避免通行.
车辆进入隧道,应在行驶车道内通行(禁止压线),且必须保证车辆顶部与隧道顶部在竖直方向的空隙不小于0.3米.
实地考察数据采集
斜坡的坡角为 , 并查得: ,
,
.
隧道的最高点C到地面距离为5.4米,两侧墙面高米,地面跨度米.车辆行驶方向的右侧车道线(宽度忽略不计)与墙面的距离为1米.
问题解决:
(1)、如图2,求涉水线离坡底的距离(精确到0.01米);(2)、在图3中建立适当的平面直角坐标系,求抛物线的解析式;(3)、限高架上标有警示语“车辆限高h米”(即最大安全限高),求h的值(精确到米).25. 如图1, , 为中点,点在上方,连接 , .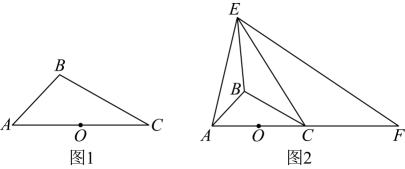 (1)、尺规作图:作点关于点的对称点(保留作图痕迹,不写作法),连接 , , 并证明:四边形为平行四边形;(2)、如图2,延长至点 , 使得 , 当点在直线的上方运动,直线的上方有异于点的动点 , 连接 , , , , 若 , 且 .
(1)、尺规作图:作点关于点的对称点(保留作图痕迹,不写作法),连接 , , 并证明:四边形为平行四边形;(2)、如图2,延长至点 , 使得 , 当点在直线的上方运动,直线的上方有异于点的动点 , 连接 , , , , 若 , 且 .①求证:;
②的长是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.