1.2矩形的性质与判定（第1课时）—北师大版数学九（上）课堂达标卷

试卷更新日期：2025-07-28 类型：同步测试

进入出卷网下载

1. 矩形具有而菱形不具有的性质是（）

A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角相等

查看试题解析
2. 如图，在矩形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点 $O$ ，则下列结论一定正确的是（）

A、 $A B = A D$ B、 $A C ⊥ B D$ C、 $A C = B D$ D、 $∠ A C B = ∠ A C D$

查看试题解析
3. 如图，将矩形 $A B C D$ 沿对角线 $B D$ 折叠，点 $A$ 落在 $A^{'}$ 处， $A^{'} D$ 交 $B C$ 于点 $E$ ．将 $△ C D E$ 沿 $D E$ 折叠，点 $C$ 落在 $△ B D E$ 内的 $C^{'}$ 处，下列结论一定正确的是（）

A、 $∠ 1 = 45 ° - α$ B、 $∠ 1 = α$ C、 $∠ 2 = 90 ° - α$ D、 $∠ 2 = 2 a$

查看试题解析
4. 如图，在矩形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O， $∠ A B D = 60 °$ ， $A B = 2$ ，则 $A C$ 的长为（　　）

A、6 B、5 C、4 D、3

查看试题解析
5. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 20 °$ ， $C D$ 为 $A B$ 边上的中线， $D E ⊥ A C$ ，则图中与 $∠ A$ 互余的角共有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

6. 如图，在矩形 $A B C D$ 中， $A B = 8, A D = 6$ ，点E、F分别是边 $A D 、 C D$ 上的动点，连接 $B E 、 E F$ ，点G为 $B E$ 的中点，点H为 $E F$ 的中点，连接 $G H$ ，则 $G H$ 的最大值是．

查看试题解析
7. 如图矩形ABCD的对角线AC和BD相交于点O，过点O的直线分别交AD和BC于点E，F，AB＝3，BC＝4，则图中阴影部分的面积为．

查看试题解析
8. 已知矩形纸片ABCD ， AB＝5，BC＝4，点P在边BC上，连接AP ，将△ABP沿AP所在的直线折叠，点B的对应点为 $B^{'}$ ，把纸片展平，连接 $B B^{'}$ ， $C B^{'}$ ，当 $△ B C B^{'}$ 为直角三角形时，线段CP的长为．

查看试题解析
9. 如图，在△ABC中，点D ， E分别是边AB ， BC的中点，点F在线段DE的延长线上，且∠BFC＝90°．若AC＝4，BC＝8，则DF的长是．

查看试题解析
10. 如图，四边形 $A B C D$ 是菱形，对角线 $A C$ ， $B D$ 相交于点 $O$ ， $E$ 是边 $C D$ 的中点，过点 $E$ 作 $E F ⊥ B D$ 于点 $F$ ， $E G ⊥ A C$ 于点 $G$ ，若 $A C = 12$ ， $B D = 16$ ，则 $F G$ 的长为．

查看试题解析

11. 如图，在矩形ABCD中，点E ， F在边BC上，连接AE ， DF ， ∠BAE＝∠CDF ．

(1)、求证：△ABE≌△DCF ．

(2)、当AB＝12，DF＝13时，求BE的长．

查看试题解析
12. 如图，将矩形ABCD沿对角线AC折叠，点B的对应点为E，AE与CD交于点F.

(1)、求证： $△ D A F ≌ △ E C F$ ；

(2)、若 $∠ F C E = 40 °$ ，求 $∠ C A B$ 的度数.

查看试题解析
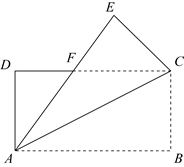13. 如图，在矩形ABCD中，AB＞2AD ，点E ， F分别在边AB ， CD上．将△ADF沿AF折叠，点D的对应点G恰好落在对角线AC上；将△CBE沿CE折叠，点B的对应点H恰好也落在对角线AC上．连接GE ， FH ．
求证：

(1)、△AEH≌△CFG；

(2)、四边形EGFH为平行四边形．

查看试题解析
14. 如图，矩形ABCD中，E是AD的中点，延长CE，BA交于点F，连接AC，DF。

(1)、求证：四边形ACDF是平行四边形；

(2)、当CF平分∠BCD时，写出BC与CD的数量关系，并说明理由。

查看试题解析
15. 如图， $O$ 为矩形 $A B C D$ 对角线 $A C$ 的中点， $E F ⊥ A C$ 于点 $O$ ，交 $A D$ ， $B C$ 于点 $E$ ， $F$ ，连接 $A F$ ， $C E$ ．

(1)、求证：四边形 $A E C F$ 为菱形；

(2)、若 $A B = 2$ ， $B C = 4$ ，求 $A E$ 的长．

查看试题解析