1.2矩形的性质与判定（第2课时）—北师大版数学九（上）课堂达标卷

试卷更新日期：2025-07-28 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，要使平行四边形ABCD是矩形，需要增加的一个条件可以是（）

A、AB∥CD B、AB=BC C、 $∠ B = ∠ D$ D、 $A C = B D$

查看试题解析
2. 在四边形 $A B C D$ 中， $A D ∥ B C ， A B = C D$ ．下列说法能使四边形 $A B C D$ 为矩形的是（）

A、 $A B ∥ C D$ B、 $A D = B C$ C、 $∠ A = ∠ B$ D、 $∠ A = ∠ D$

查看试题解析
3. 如图，在菱形ABCD中，E，F，G，H 分别是边AB，BC，CD 和DA 的中点，连接EF，FG，GH和 HE.若EH=2EF，则下列结论正确的是( ).

A、 $A B = \sqrt{2} E F$ B、AB=2EF C、 $A B = \sqrt{3} E F$ D、 $A B = \sqrt{5} E F$

查看试题解析
4. 如图，在Rt△ABC中，∠BCA＝90°，取边AB上任意一点D（不与点A重合），连结DC ，作▱ADCE ， AC与DE交于点F ，则下列结论中正确的是（）
①当点D位置变化时，F始终为AC中点；
②当D为AB中点时，线段DE取得最小值；
③当CD⟂AB时，四边形ADCE为矩形；

A、①② B、①③ C、②③ D、①②③

查看试题解析
5. 如图，AC ， BD是四边形ABCD的对角线，点E，F分别是AD，BC的中点，点M，N分别是AC，BD的中点．下列说法中不正确的是（）

A、四边形EMFN一定是平行四边形 B、若 $A C ⊥ B D$ ，则四边形EMFN是矩形 C、若 $A B = C D$ ，则四边形EMFN是菱形 D、若 $∠ A B C + ∠ D C B = 9 0^{°}$ ，则四边形EMFN是矩形

查看试题解析

二、填空题

6. 如图，四边形 $A B C D$ 为平行四边形，延长 $A D$ 到 $E$ ，使 $D E = A D$ ，连结 $E B$ ， $E C$ ， $D B$ ，要使四边形 $D B C E$ 成为矩形，可添加一个条件是． (只要写出一个条件即可)

查看试题解析
7. 如图，四边形 $A B C D$ 是平行四边形，请你添加一个条件，使 $□ A B C D$ 为矩形（任意添加一个符合题意的条件即可）．

查看试题解析
8. 如图，将平行四边形 $A B C D$ 的边 $D C$ 延长线到点 $E$ ，使 $C E = D C$ ，连接 $A E$ ，交 $B C$ 于点 $F$ ．添加一个条件，使四边形 $A B E C$ 是矩形．下列四个条件：① $∠ D A C = ∠ E A C$ ；② $A D = A E$ ；③ $A B = A D$ ；④ $∠ A F C = 2 ∠ A B C$ 中，你认为可选择的是．（填上所有满足条件的序号）

查看试题解析
9. 如图，在 $△ A B C$ 中， $D ， E ， F$ 分别是 $A B ， B C$ ， $A C$ 边的中点，请添加一个条件，使四边形 $B E F D$ 为矩形．（填一个即可）

查看试题解析
10. 如图，在菱形 $A B C D$ 中，边长为1， $∠ A = 60^{\circ}$ 顺次连接菱形 $A B C D$ 各边中点，可得四边形 $A_{1} B_{1} C_{1} D_{1}$ ；顺次连接四边形 $A_{1} B_{1} C_{1} D_{1}$ 各边中点，可得四边形 $A_{2} B_{2} C_{2} D_{2}$ ；顺次连接四边形 $A_{2} B_{2} C_{2} D_{2}$ 边中点，可得四边形 $A_{3} B_{3} C_{3} D_{3} \dots$ ；按此规律继续下去，则四边形 $A_{8} B_{8} C_{8} D_{8}$ 的面积是．

查看试题解析

三、解答题

11. 如图

(1)、如图①，将平行四边形纸片ABCD的四个角向内折叠，恰好拼成一个无缝隙、无重叠的四边形EFGH ．判断四边形EFGH的形状，并说明理由；

(2)、如图②，已知▱ABCD能按照图①的方式对折成一个无缝隙、无重叠的四边形MNPQ ，其中，点M在AD上，点N在AB上，点P在BC上，点Q在CD上．请用直尺和圆规确定点M的位置．（不写作法，保留作图痕迹）

查看试题解析
12. 如图，在 $▱ A B C D$ 中， $∠ B A D$ 的平分线交 $B C$ 于点E， $∠ D C B$ 的平分线交 $A D$ 于点F，点G，H分别是 $A E$ 和 $C F$ 的中点．

(1)、求证： $△ A B E ≌ △ C D F$ ；

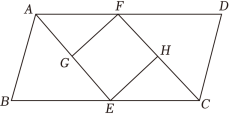(2)、连接 $E F$ ．若 $E F = A F$ ，请判断四边形 $G E H F$ 的形状，并证明你的结论．

查看试题解析
13. 如图，△ABC中，D是BC边上一点，E是AD的中点，过点A作BC的平行线交BE的延长线于F，且AF=CD，连接CF．

(1)、求证：△AEF≌△DEB；

(2)、若AB=AC，试判断四边形ADCF的形状，并证明你的结论．

查看试题解析
14. 如图，在 $△ A B C$ 中， $A B = A C$ ， D是 $B C$ 的中点， $C E ∥ A D$ ， $A E ⊥ A D$ ， $E F ⊥ A C$ ．

(1)、求证：四边形 $A D C E$ 是矩形；

(2)、若 $B C = 4, C E = 3$ ，求 $E F$ 的长．

查看试题解析
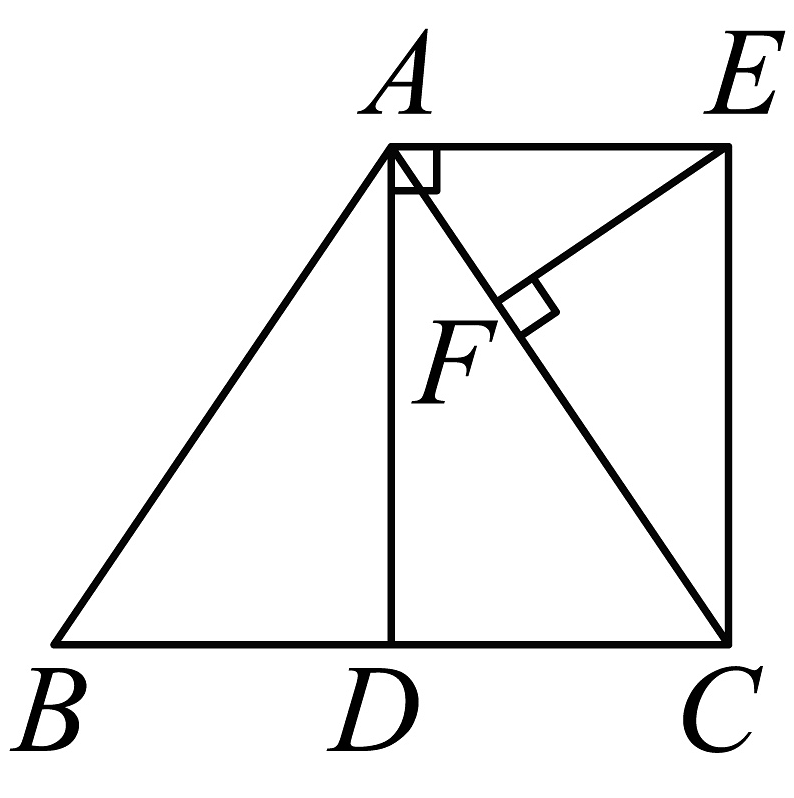15. 康康在学习了矩形定义及判定定理1后，继续探究其它判定定理.

(1)、实践与操作
①任意作两条相交的直线，交点记为O；
②以点O为圆心，适当长为半径画弧，在两条直线上分别截取相等的四条线段；OA ， OB ， OC ， OD
③顺次连结所得的四点得到四边形 $A B C D$ .
于是可以直接判定四边形 $A B C D$ 是平行四边形，则该判定定理是：.

(2)、猜想与证明
通过和同伴交流，他们一致认为四边形 $A B C D$ 是矩形，于是猜想得到了矩形的另外一种判定方法：对角线相等的平行四边形是矩形.并写出了以下已知、求证，请你完成证明过程.
已知：如图，四边形 $A B C D$ 是平行四边形， $A C = B D$ .
求证：四边形 $A B C D$ 是矩形.

查看试题解析