1.2矩形的性质与判定（第3课时）—北师大版数学九（上）课堂达标卷

试卷更新日期：2025-07-28 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $A C = 12$ ， $B C = 5$ ，点P是边 $A B$ 上任意一点，过点P作 $P D ⊥ A C$ ， $P E ⊥ B C$ ，垂足分别为点D，E，连接 $D E$ ，则 $D E$ 的最小值是（）

A、 $\frac{13}{2}$ B、 $\frac{60}{13}$ C、 $\frac{12}{5}$ D、 $\frac{30}{13}$

查看试题解析
2. 如图，在Rt△ABC中，∠A＝90°，M为BC的中点，H为AB上一点，过点C作CG∥AB，交HM的延长线于点G，若AC＝8，AB＝6，则四边形ACGH周长的最小值是（）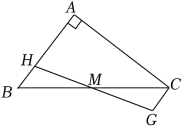

A、24 B、22 C、20 D、18

查看试题解析
3. 如图，在矩形 $A B C D$ 中， E、F分别是 $A B 、 C D$ 边的中点， G为 $A D$ 边上的一点，将矩形沿 $B G$ 翻折使得点A落在 $E F$ 上，点A对应点为点 $A^{'}$ ．若 $A B = 6$ ，则四边形 $A B A^{'} G$ 的面积为（）

A、9 B、 $12 \sqrt{3}$ C、15 D、 $8 \sqrt{5}$

查看试题解析
4. 如图，在四边形ABCD中， $A C, B D$ 相交于点 $O$ ，且 $O A = O B = O C = O D$ ，动点E从点 $B$ 开始，沿折线 $B - A - D$ 运动至点 $D$ 停止，CE与BD相交于点 $N$ ，点 $F$ 是线段CE的中点，连接OF ，有下列结论：①四边形ABCD是矩形；②当点 $B$ 在边AB上，且 $C D = 4 O F$ 时，点E是AB的中点；③当 $A B = 3, B C = 4$ 时，线段OF长度的最大值为2；④当点E在边AB上，且 $∠ C O F = 6 0^{°}$ 时， $△ O F N$ 是等边三角形．其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F ，连结BF交AC于点M ，连结DE、BO.若∠COB=60°，FO=FC ，则下列结论中正确结论的个数是（）
①DE=EF；②四边形DFBE是菱形；③BM=3FM；④ $S_{△ F O M} : S_{矩形 A B C D}$ =1：14.

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

6. 如图，在 $Rt Δ A B C$ 中， $∠ B A C = 90 °$ ，且 $B A = 3$ ， $A C = 4$ ，点 $D$ 是斜边 $B C$ 上的一个动点，过点 $D$ 分别作 $D M ⊥ A B$ 于点 $M$ ， $D N ⊥ A C$ 于点 $N$ ，连接 $M N$ ，则线段 $M N$ 的最小值为．

查看试题解析
7. 如图，∠MON＝90°，长方形ABCD的顶点B、C分别在边OM、ON上，当B在边OM上运动时，C随之在边ON上运动，若CD＝5，BC＝24，运动过程中，点D到点O的最大距离为.

查看试题解析
8. 如图，已知平行四边形 $A B C D$ 的对角线 $A C ， B D$ 相交于点 $O ， △ A O B$ 是等边三角形， $A B = 4 c m$ ，则平行四边形 $A B C D$ 的面积为 ${c m}^{2}$ ．

查看试题解析
9. 如图，已知 $A B ∥ C D$ ， $A B = C D$ ， $∠ A = ∠ D$ ， E是 $A B$ 边的中点，F为 $A D$ 边上一点， $∠ D F C = 2 ∠ B C E$ ，若 $C E = 4$ ， $C F = 5$ ，则 $A F$ 的值为．

查看试题解析
10. 如图，四边形 $A B C D$ 的两条对角线 $A C$ ， $B D$ 互相垂直， $A C = 4$ ， $B D = 6$ ，则 $A D + B C$ 的最小值是．

查看试题解析

三、解答题

11. 如图，在 $△ A B C$ 中， $∠ A B C = 9 0^{\circ}, O$ 是AC的中点.延长BO至点D，使（ $O D = O B .$ 连接AD，CD.记. $A B = a, B C = b, △ A O B$ 的周长为 $l_{1}, △ B O C$ 的周长为 $l_{2},$ ，四边形ABCD的周长为l₃.

(1)、求证：四边形ABCD是矩形；

(2)、若 $l_{2} - l_{1} = 2, l_{3} = 28,$ 求AC的长.

查看试题解析
12. 如图，在平行四边形 $A B C D$ 中， $E$ 为线段 $C D$ 的中点，连接 $A C$ ， $A E$ ，延长 $A E$ ， $B C$ 交于点 $F$ ，连接 $D F$ ， $∠ A C F = 90 °$ ．

(1)、求证：四边形 $A C F D$ 是矩形；

(2)、若 $C D = 13$ ， $C F = 5$ ，求四边形 $A B C E$ 的面积．

查看试题解析
13. 如图所示，菱形ABCD对角线AC，BD相交于点O，E是AD的中点，点F，G在AB上，EF⊥AB，OG∥EF.

(1)、求证：四边形OEFG是矩形.

(2)、若AD=10，EF=4，求OE和BG的长.

查看试题解析
14. 如图，O是矩形ABCD的对角线的交点，E，F，G，H分别是OA，OB，OC，OD上的点，且AE＝BF＝CG＝DH.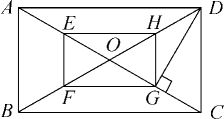

(1)、求证：四边形EFGH是矩形；

(2)、若E，F，G，H分别是OA，OB，OC，OD的中点，且DG⊥AC，OF＝2cm，求矩形ABCD的面积．

查看试题解析
15. 阅读下面材料：
在数学课上，老师请同学思考如下问题：如图1，我们把一个四边形ABCD的四边中点E，F，G，H依次连接起来得到的四边形EFGH是平行四边形吗？
小敏在思考问题是，有如下思路：连接AC．
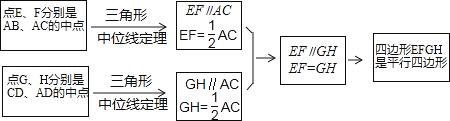
结合小敏的思路作答

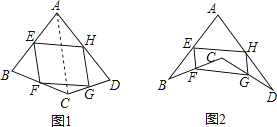(1)、若只改变图1中四边形ABCD的形状（如图2），则四边形EFGH还是平行四边形吗？说明理由；参考小敏思考问题方法解决一下问题：

(2)、如图2，在（1）的条件下，若连接AC，BD．
①当AC与BD满足什么条件时，四边形EFGH是菱形，写出结论并证明；
②当AC与BD满足什么条件时，四边形EFGH是矩形，直接写出结论．

查看试题解析