1.3正方形的性质与判定(第1课时)—北师大版数学九(上)课堂达标卷
试卷更新日期:2025-07-28 类型:同步测试
一、选择题
-
1. 下列说法正确的是( )A、菱形的四个内角都是直角 B、矩形的对角线互相垂直 C、正方形的每一条对角线平分一组对角 D、平行四边形是轴对称图形2. 如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,),则点C的坐标为( )
 A、(﹣1,﹣) B、( , ﹣1) C、(﹣1,) D、(﹣ , 1)3. 如图,三个边长相同的正方形叠放在一起,M,N是其中两个正方形的中心,阴影部分的面积和是4,则正方形的边长为( )
A、(﹣1,﹣) B、( , ﹣1) C、(﹣1,) D、(﹣ , 1)3. 如图,三个边长相同的正方形叠放在一起,M,N是其中两个正方形的中心,阴影部分的面积和是4,则正方形的边长为( ) A、2 B、 C、 D、44. 如图,在正方形ABCD中,AB=5,点M在CD的边上,且DM=2,△AEM与△ADM关于AM所在的直线对称,将△ADM按顺时针方向绕点A旋转90°得到△ABF,连接EF,则线段EF的长为( )
A、2 B、 C、 D、44. 如图,在正方形ABCD中,AB=5,点M在CD的边上,且DM=2,△AEM与△ADM关于AM所在的直线对称,将△ADM按顺时针方向绕点A旋转90°得到△ABF,连接EF,则线段EF的长为( ) A、 B、 C、 D、5. 如图,点P是正方形的对角线上一点,于点于点F,连接 , 给出下列四个结论:
A、 B、 C、 D、5. 如图,点P是正方形的对角线上一点,于点于点F,连接 , 给出下列四个结论:①;②;③;④ , 其中正确的是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
6. 如图,在平面直角坐标系中,正方形的边在x轴上,点B的坐标为 . 点E在边上.将沿折叠,点D落在点F处.若点F的坐标为 . 则点E的坐标为 .
 7. 以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是 .8. 如图,在边长为2的正方形中,E,F分别是上的动点,M,N分别是的中点,则的最大值为 .
7. 以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是 .8. 如图,在边长为2的正方形中,E,F分别是上的动点,M,N分别是的中点,则的最大值为 .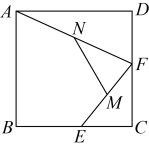 9. 如图,正方形的边长为 , 点在边上,且 , 为对角线上一动点,连接 , , 则的最小值为 .
9. 如图,正方形的边长为 , 点在边上,且 , 为对角线上一动点,连接 , , 则的最小值为 . 10. 如图,正方形ABCD的边长为1,M、N是边BC、CD上的动点.若 , 则MN的最小值为 .
10. 如图,正方形ABCD的边长为1,M、N是边BC、CD上的动点.若 , 则MN的最小值为 .
三、解答题
-
11. 如图, 正方形ABCD中, 点E, F 分别在AB, CD上, 且BE=DF .
 (1)、求证:四边形AECF 是平行四边形;(2)、 连接EF, 若BC=12, BE=5, 求EF的长.12. 在综合实践活动中,同学们将对学校的一块正方形花园ABCD进行测量规划使用,如图,点E、F处是它的两个门,且DE=CF,要修建两条直路AF、BE,AF与BE相交于点O(两个门E、F的大小忽略不计).
(1)、求证:四边形AECF 是平行四边形;(2)、 连接EF, 若BC=12, BE=5, 求EF的长.12. 在综合实践活动中,同学们将对学校的一块正方形花园ABCD进行测量规划使用,如图,点E、F处是它的两个门,且DE=CF,要修建两条直路AF、BE,AF与BE相交于点O(两个门E、F的大小忽略不计). (1)、请问这两条路是否等长?它们有什么位置关系,说明理由;(2)、同学们测得AD=4米,AE=3米,根据实际需要,某小组同学想在四边形OBCF地上再修一条2.5米长的直路,这条直路的一端在门F处,另一端P在已经修建好的路段OB或花园的边界BC上,并且另一端P与点B处的距离不少于1.5米,请问能否修建成这样的直路,若能,能修建几条,并说明理由.13. 如图,E, F是正方形 ABCD 的对角线 BD 上的两点, , , 连接 AE,AF,CE,CF.
(1)、请问这两条路是否等长?它们有什么位置关系,说明理由;(2)、同学们测得AD=4米,AE=3米,根据实际需要,某小组同学想在四边形OBCF地上再修一条2.5米长的直路,这条直路的一端在门F处,另一端P在已经修建好的路段OB或花园的边界BC上,并且另一端P与点B处的距离不少于1.5米,请问能否修建成这样的直路,若能,能修建几条,并说明理由.13. 如图,E, F是正方形 ABCD 的对角线 BD 上的两点, , , 连接 AE,AF,CE,CF. (1)、 求证:.(2)、 若四边形 AECF 的周长为 , 求 EF 的长.
(1)、 求证:.(2)、 若四边形 AECF 的周长为 , 求 EF 的长.

