1.3正方形的性质与判定(第2课时)—北师大版数学九(上)课堂达标卷
试卷更新日期:2025-07-28 类型:同步测试
一、选择题
-
1. 下列说法中,正确的是( )A、对角线互相垂直的四边形是菱形 B、一组邻边相等的平行四边形是正方形 C、对角线互相平分且垂直的四边形是菱形 D、对角线相等的四边形是矩形2. 如图,四边形ABCD是平行四边形,下列结论中错误的是( )
 A、当 , 是矩形 B、当 , 是矩形 C、当 , 是菱形 D、当 , 是正方形3. 如图,点E、F、G、H分别是四边形边、、、的中点.则正确的是( )
A、当 , 是矩形 B、当 , 是矩形 C、当 , 是菱形 D、当 , 是正方形3. 如图,点E、F、G、H分别是四边形边、、、的中点.则正确的是( )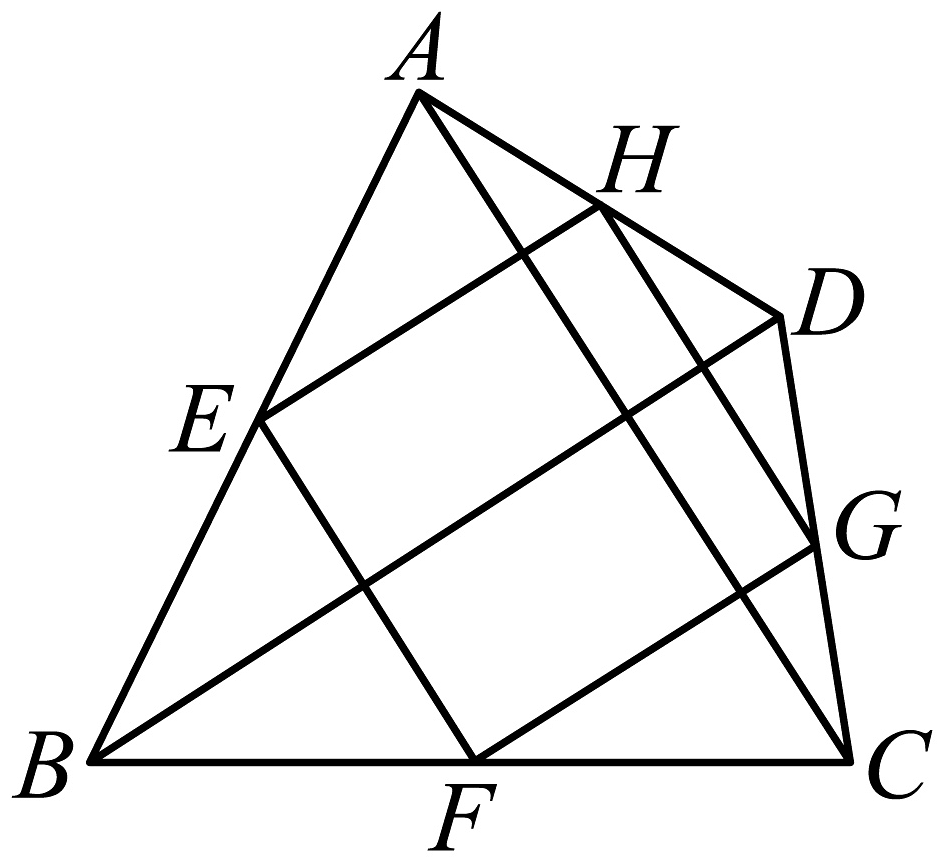 A、若 , 则四边形为矩形 B、若 , 则四边形为菱形 C、若是平行四边形,则与互相平分 D、若是正方形,则与互相垂直且相等4. 如图,已知四边形ABCD是平行四边形,下列说法正确的是( )
A、若 , 则四边形为矩形 B、若 , 则四边形为菱形 C、若是平行四边形,则与互相平分 D、若是正方形,则与互相垂直且相等4. 如图,已知四边形ABCD是平行四边形,下列说法正确的是( ) A、若 , 则是菱形 B、若 , 则是矩形 C、若 , 则是正方形 D、若 , 则是正方形5. 如图,已知四边形为正方形, , 为对角线上一点,连接 , 过点作 , 交的延长线于点 , 以 , 为邻边作矩形 , 连接 . 以下结论:①矩形是正方形;②;③平分;④ . 其中结论正确的序号有( ).
A、若 , 则是菱形 B、若 , 则是矩形 C、若 , 则是正方形 D、若 , 则是正方形5. 如图,已知四边形为正方形, , 为对角线上一点,连接 , 过点作 , 交的延长线于点 , 以 , 为邻边作矩形 , 连接 . 以下结论:①矩形是正方形;②;③平分;④ . 其中结论正确的序号有( ). A、①③④ B、①②④ C、①②③ D、①②③④
A、①③④ B、①②④ C、①②③ D、①②③④二、填空题
-
6. 如图,四边形为正方形,点E是的中点,将正方形沿折叠,得到点B的对应点为点F,延长交线段于点P,若 , 则的长度为 .
 7. 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点处,当为直角三角形时,BE的长为
7. 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点处,当为直角三角形时,BE的长为 8. 如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,则正方形ABCD的边长为 .
8. 如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,则正方形ABCD的边长为 . 9. 正方形 的边长为4,点 在对角线 上(可与点 重合), ,点 在正方形的边上.下面四个结论中,
9. 正方形 的边长为4,点 在对角线 上(可与点 重合), ,点 在正方形的边上.下面四个结论中,①存在无数个四边形 是平行四边形;
②存在无数个四边形 是菱形;
③存在无数个四边形 是矩形;
④至少存在一个四边形 是正方形.
所有正确结论的序号是 .
10. 在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是 .三、解答题
-
11. 如图,∠ACB=∠AED=90°,AC=FE , AB平分∠CAE , AB∥DF .
 (1)、求证:四边形ABDF是平行四边形;(2)、过点B作BG⊥AE于点G , 若CB=AF , 请直接写出四边形BGED的形状.12. 如图,点E为正方形外一点, , 将绕A点逆时针方向旋转得到的延长线交于H点.
(1)、求证:四边形ABDF是平行四边形;(2)、过点B作BG⊥AE于点G , 若CB=AF , 请直接写出四边形BGED的形状.12. 如图,点E为正方形外一点, , 将绕A点逆时针方向旋转得到的延长线交于H点.
(1)试判定四边形的形状,并说明理由;
(2)已知 , 求的长.
13. 如图,在 中, 的角平分线交 于点D, .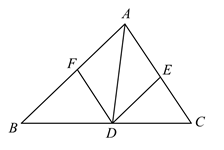 (1)、试判断四边形 的形状,并说明理由;(2)、若 ,且 ,求四边形 的面积.
(1)、试判断四边形 的形状,并说明理由;(2)、若 ,且 ,求四边形 的面积.