第一章《特殊平行四边形》A卷—北师大版数学九年级上册单元检测
试卷更新日期:2025-07-28 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 下列命题中,假命题是( )A、矩形的对角线相等 B、菱形的对角线互相垂直 C、正方形的对角线相等且互相垂直 D、平行四边形的对角线相等2. 如图,在平面直角坐标系中,正方形的边长为5,边在轴上. . 若将正方形绕点逆时针旋转 . 得到正方形 . 则点的坐标为( )
 A、(-3,5) B、(5,-3) C、(-2,5) D、(5,-2)3. 如图,在矩形中,点在边上, , 连接 , 若 , , 则的长为( )
A、(-3,5) B、(5,-3) C、(-2,5) D、(5,-2)3. 如图,在矩形中,点在边上, , 连接 , 若 , , 则的长为( )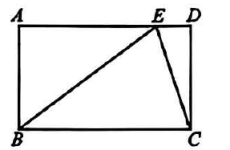 A、1 B、5 C、2 D、4. 一个矩形的一条对角线长为10,两条对角线的一个交角为60°.则这个矩形的面积是( )A、25 B、25 C、25 D、505. 如图,将正方形ABCD沿EF折叠,使得点A与对角线的交点O重合,EF为折痕,则的值为( )
A、1 B、5 C、2 D、4. 一个矩形的一条对角线长为10,两条对角线的一个交角为60°.则这个矩形的面积是( )A、25 B、25 C、25 D、505. 如图,将正方形ABCD沿EF折叠,使得点A与对角线的交点O重合,EF为折痕,则的值为( ) A、 B、 C、 D、6. 如图,在四边形ABCD中,对角线AC与BD互相垂直平分,AB=3,则四边形ABCD的周长为( )
A、 B、 C、 D、6. 如图,在四边形ABCD中,对角线AC与BD互相垂直平分,AB=3,则四边形ABCD的周长为( ) A、6 B、9 C、12 D、187. 如图,在Rt△ABC中,∠ACB=90°,将△ABC沿CB方向向右平移至△EGF处,使EF恰好过边AB的中点D,连接CD,若CD=1,则GE= ( )
A、6 B、9 C、12 D、187. 如图,在Rt△ABC中,∠ACB=90°,将△ABC沿CB方向向右平移至△EGF处,使EF恰好过边AB的中点D,连接CD,若CD=1,则GE= ( ) A、3 B、2 C、1 D、8. 小美同学按如下步骤作四边形:(1)画;(2)以点A为圆心,1个单位长为半径画弧,分别交 , 于点B , D;(3)分别以点B , D为圆心,1个单位长为半径画弧,两弧交于点C;(4)连接 , , . 若 , 则的大小是( )
A、3 B、2 C、1 D、8. 小美同学按如下步骤作四边形:(1)画;(2)以点A为圆心,1个单位长为半径画弧,分别交 , 于点B , D;(3)分别以点B , D为圆心,1个单位长为半径画弧,两弧交于点C;(4)连接 , , . 若 , 则的大小是( ) A、 B、 C、 D、9. 如图,菱形ABCD的对角线AC , BD相交于点O , E是AB的中点,连接OE . 若OE=3,则菱形的边长为( )
A、 B、 C、 D、9. 如图,菱形ABCD的对角线AC , BD相交于点O , E是AB的中点,连接OE . 若OE=3,则菱形的边长为( ) A、6 B、8 C、10 D、1210. 如图,在正方形ABCD中,分别以点A和B为圆心,以大于AB的长为半径作弧,两弧相交于点E和F , 作直线EF , 再以点A为圆心,以AD的长为半径作弧交直线EF于点G(点G在正方形ABCD内部),连接DG并延长交BC于点K . 若BK=2,则正方形ABCD的边长为 ( )
A、6 B、8 C、10 D、1210. 如图,在正方形ABCD中,分别以点A和B为圆心,以大于AB的长为半径作弧,两弧相交于点E和F , 作直线EF , 再以点A为圆心,以AD的长为半径作弧交直线EF于点G(点G在正方形ABCD内部),连接DG并延长交BC于点K . 若BK=2,则正方形ABCD的边长为 ( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 如图,在平行四边形ABCD中,对角线AC , BD相交于点O , 请添加一个条件 , 使平行四边形ABCD为菱形。
 12. 一个矩形相邻两边的长分别为2,m , 则这个矩形的面积是 .13. 如图,在菱形ABCD中,对角线AC , BD相交于点O , 请添加一个条件 , 使得菱形ABCD为正方形.
12. 一个矩形相邻两边的长分别为2,m , 则这个矩形的面积是 .13. 如图,在菱形ABCD中,对角线AC , BD相交于点O , 请添加一个条件 , 使得菱形ABCD为正方形. 14. 如图,在菱形中, , 对角线的长为 , 是的中点,是上一点,连接 . 若 , 则的长为 .
14. 如图,在菱形中, , 对角线的长为 , 是的中点,是上一点,连接 . 若 , 则的长为 . 15. 如图,将矩形纸片沿边折叠,使点在边中点处.若 , 则 .
15. 如图,将矩形纸片沿边折叠,使点在边中点处.若 , 则 .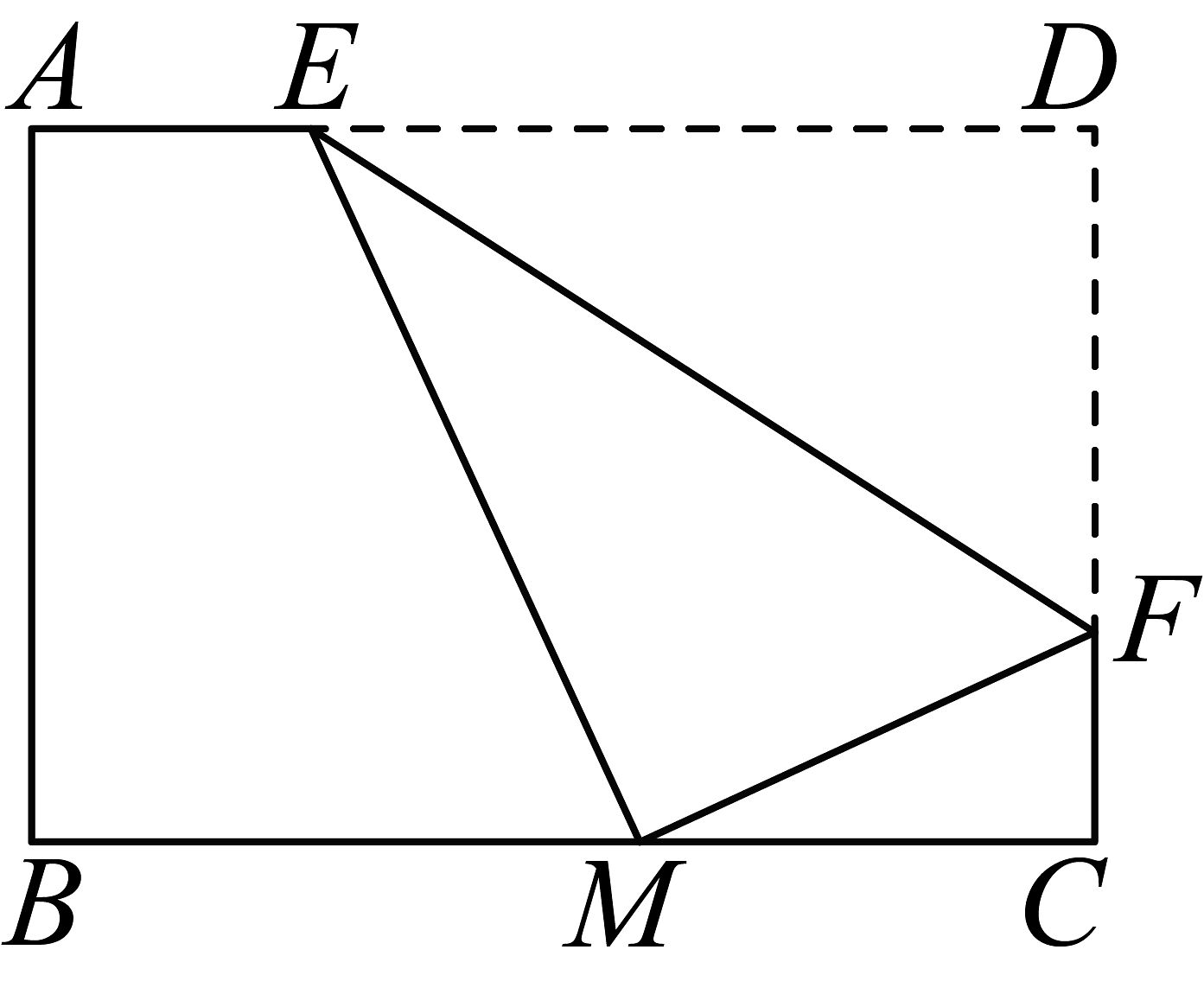 16. 如图,在中, . P为边上一动点,作于点D,于点E,则的最小值为 .
16. 如图,在中, . P为边上一动点,作于点D,于点E,则的最小值为 .
三、解答题(共8题,共72分)
-
17. 如图,在中,为对角线上的中点,连接 , 且 , 垂足为 . 延长至 , 使 , 连接 , , 且交于点 .
 (1)、求证:是菱形;(2)、若 , 求的面积.18. 如图,为菱形的对角线,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹)
(1)、求证:是菱形;(2)、若 , 求的面积.18. 如图,为菱形的对角线,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹) (1)、如图,过点作的垂线;(2)、如图 , 点为线段的中点,过点作的平行线.19. 如图,矩形的对角线 , 相交于点O, .
(1)、如图,过点作的垂线;(2)、如图 , 点为线段的中点,过点作的平行线.19. 如图,矩形的对角线 , 相交于点O, . (1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.20. 已知:如图,四边形为正方形,点E在的延长线上,连接 .
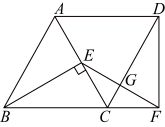
(1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.20. 已知:如图,四边形为正方形,点E在的延长线上,连接 . (1)、求证:;(2)、若 , 求证: .21. 如图,的中线BD,CE交于点 , 点F,G分别是OB,OC的中点.
(1)、求证:;(2)、若 , 求证: .21. 如图,的中线BD,CE交于点 , 点F,G分别是OB,OC的中点. (1)、求证:四边形DEFG是平行四边形;(2)、当BD=CE时,求证:是矩形.22. 已知点 在正方形 ABCD 内,点 E 在边 AD 上,BE 是线段的垂直平分线,连接.
(1)、求证:四边形DEFG是平行四边形;(2)、当BD=CE时,求证:是矩形.22. 已知点 在正方形 ABCD 内,点 E 在边 AD 上,BE 是线段的垂直平分线,连接. (1)、 如图 1, 若 的延长线经过点 D, , 求 AB 的长;(2)、 如图 2, 点 F 是 的延长线与 CD 的交点,连接 .
(1)、 如图 1, 若 的延长线经过点 D, , 求 AB 的长;(2)、 如图 2, 点 F 是 的延长线与 CD 的交点,连接 .(a) 求证: ;
(b) 如图 3, 设 AF, BE 相交于点 G, 连接 , 若 , 判断 的形状,并说明理由.
23.
(1)、(阅读理解)如图1, , 的面积与 的面积相等吗?为什么?
 (2)、(类比探究)问题①,如图2,在正方形 的右侧作等腰 , , ,连接 ,求 的面积.
(2)、(类比探究)问题①,如图2,在正方形 的右侧作等腰 , , ,连接 ,求 的面积.
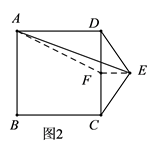
解:过点 作 于点 ,连接 .
请将余下的求解步骤补充完整.
(3)、(拓展应用)问题②,如图3,在正方形 的右侧作正方形 ,点 , , 在同一直线上, ,连接 , , ,直接写出 的面积.
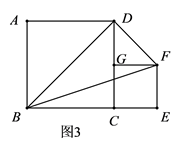 24. 【问题背景】在学习了平行四边形后,某数学兴趣小组研究了有一个内角为60°的平行四边形的折叠问题.其探究过程如下:
24. 【问题背景】在学习了平行四边形后,某数学兴趣小组研究了有一个内角为60°的平行四边形的折叠问题.其探究过程如下: (1)、【探究发现】如图①,在▱ABCD中,∠A=60°,AB>AD , E为边AD的中点,点F在边DC上,且DF=DE , 连接EF , 将△DEF沿EF翻折得到△GEF , 点D的对称点为点G . 小组成员发现四边形DEGF是一个特殊的四边形,请判断该四边形的形状,不需要说明理由.(2)、【探究证明】取图①中的边BC的中点M , 点N在边AB上,且BN=BM , 连接MN , 将△BMN沿MN翻折得到△HMN , 点B的对称点为点H , 连接FH , GN , 如图②,求证:四边形GFHN是平行四边形.(3)、【探究提升】在图②中,四边形GFHN能否成为轴对称图形.如果能,直接写出的值;如果不能,说明理由.
(1)、【探究发现】如图①,在▱ABCD中,∠A=60°,AB>AD , E为边AD的中点,点F在边DC上,且DF=DE , 连接EF , 将△DEF沿EF翻折得到△GEF , 点D的对称点为点G . 小组成员发现四边形DEGF是一个特殊的四边形,请判断该四边形的形状,不需要说明理由.(2)、【探究证明】取图①中的边BC的中点M , 点N在边AB上,且BN=BM , 连接MN , 将△BMN沿MN翻折得到△HMN , 点B的对称点为点H , 连接FH , GN , 如图②,求证:四边形GFHN是平行四边形.(3)、【探究提升】在图②中,四边形GFHN能否成为轴对称图形.如果能,直接写出的值;如果不能,说明理由.