第一章《特殊平行四边形》B卷—北师大版数学九年级上册单元检测
试卷更新日期:2025-07-28 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 已知四边形ABCD是平行四边形,下列条件中,不能判定为矩形的是( )A、 B、 C、 D、2. 如图,直线a∥b , 矩形ABCD的顶点A在直线b上,若∠2=41°,则∠1的度数为( )
 A、41° B、51° C、49° D、59°3. 如图,以点A为圆心,适当的长为半径画弧,交两边于点M , N , 再分别以M、N为圆心,的长为半径画弧,两弧交于点B , 连接 . 若 , 则( )
A、41° B、51° C、49° D、59°3. 如图,以点A为圆心,适当的长为半径画弧,交两边于点M , N , 再分别以M、N为圆心,的长为半径画弧,两弧交于点B , 连接 . 若 , 则( ) A、 B、 C、 D、4. 如图,正方形由四个全等的直角三角形( , , , )和中间一个小正方形组成,连接 . 若 , , 则( )
A、 B、 C、 D、4. 如图,正方形由四个全等的直角三角形( , , , )和中间一个小正方形组成,连接 . 若 , , 则( ) A、5 B、 C、 D、45. 如图,矩形ABCD中, , , 动点E , F分别从点A , C同时出发,以每秒1个单位长度的速度沿AB , CD向终点B , D运动,过点E , F作直线l , 过点A作直线l的垂线,垂足为G , 则AG的最大值为( )
A、5 B、 C、 D、45. 如图,矩形ABCD中, , , 动点E , F分别从点A , C同时出发,以每秒1个单位长度的速度沿AB , CD向终点B , D运动,过点E , F作直线l , 过点A作直线l的垂线,垂足为G , 则AG的最大值为( )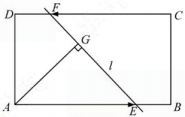 A、 B、 C、2 D、16. 如图,在边长为4的正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE , AF , AM平分∠EAF交CD于点M . 若BE=DF=1,则DM的长度为( )
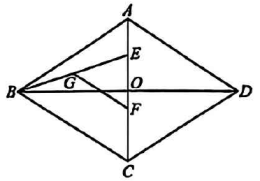
A、 B、 C、2 D、16. 如图,在边长为4的正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE , AF , AM平分∠EAF交CD于点M . 若BE=DF=1,则DM的长度为( ) A、2 B、 C、 D、7. 如图,在中, , 相交于点 , , . 过点作的垂线交于点 , 记长为 , 长为 . 当 , 的值发生变化时,下列代数式的值不变的是( )
A、2 B、 C、 D、7. 如图,在中, , 相交于点 , , . 过点作的垂线交于点 , 记长为 , 长为 . 当 , 的值发生变化时,下列代数式的值不变的是( ) A、 B、 C、 D、8. 小明同学手中有一张矩形纸片ABCD , AD=12cm , CD=10cm , 他进行了如下操作:
A、 B、 C、 D、8. 小明同学手中有一张矩形纸片ABCD , AD=12cm , CD=10cm , 他进行了如下操作:第一步,如图①,将矩形纸片对折,使AD与BC重合,得到折痕MN , 将纸片展平.
第二步,如图②,再一次折叠纸片,把△ADN沿AN折叠得到△AD'N , AD'交折痕MN于点E , 则线段EN的长为( )
 A、8cm B、 C、 D、9. 如图,在中, , , . A点P从点A出发、以的速度沿运动,同时点Q从点C出发,以的速度沿往复运动,当点P到达端点D时,点Q随之停止运动.在此运动过程中,线段出现的次数是( )
A、8cm B、 C、 D、9. 如图,在中, , , . A点P从点A出发、以的速度沿运动,同时点Q从点C出发,以的速度沿往复运动,当点P到达端点D时,点Q随之停止运动.在此运动过程中,线段出现的次数是( ) A、3 B、4 C、5 D、610. 如图,边长为6的正方形中,M为对角线上的一点,连接并延长交于点P.若 , 则的长为( )
A、3 B、4 C、5 D、610. 如图,边长为6的正方形中,M为对角线上的一点,连接并延长交于点P.若 , 则的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 如图,在菱形中,对角线与相交于点 , 点在线段上, , 点在线段上, , 连接 , 点为的中点,连接 , 则的长为 .
 12. 如图,在正方形ABCD中,若面积周长则=.
12. 如图,在正方形ABCD中,若面积周长则=.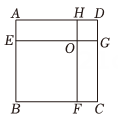 13. 如图,在平面直角坐标系xOy中,正方形ABCD的对角线AC、BD相交于原点O . 若点A的坐标是(2,1),则点C的坐标是 .
13. 如图,在平面直角坐标系xOy中,正方形ABCD的对角线AC、BD相交于原点O . 若点A的坐标是(2,1),则点C的坐标是 . 14. 矩形ABCD的面积是90,对角线AC , BD交于点O , 点E是BC边的三等分点,连接DE , 点P是DE的中点,OP=3,连接CP , 则PC+PE的值为 .15. 如图,在平面直角坐标系中,正方形ABCD的边AB在x轴上,点A的坐标为(-2,0),点E在边CD上.将沿BE折叠,点C落在点F处.若点F的坐标为(0,6),则点E的坐标为.
14. 矩形ABCD的面积是90,对角线AC , BD交于点O , 点E是BC边的三等分点,连接DE , 点P是DE的中点,OP=3,连接CP , 则PC+PE的值为 .15. 如图,在平面直角坐标系中,正方形ABCD的边AB在x轴上,点A的坐标为(-2,0),点E在边CD上.将沿BE折叠,点C落在点F处.若点F的坐标为(0,6),则点E的坐标为. 16. 如图,在矩形纸片ABCD中, , AD=2,E为边AD的中点,点F在边CD上,连接EF , 将△DEF沿EF翻折,点D的对应点为D' , 连接BD' . 若BD'=2,则DF= .
16. 如图,在矩形纸片ABCD中, , AD=2,E为边AD的中点,点F在边CD上,连接EF , 将△DEF沿EF翻折,点D的对应点为D' , 连接BD' . 若BD'=2,则DF= .
三、解答题(共8题,共72分)
-
17. 如图,在中,点E , F分别在 , 的延长线上,且 , 连接与交于点M , 连接 , .
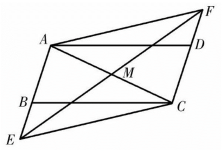 (1)、求证:;(2)、若 , , 求四边形的周长.18. 如图,正方形中,点 , 分别在 , 上,且 , 与相交于点 .
(1)、求证:;(2)、若 , , 求四边形的周长.18. 如图,正方形中,点 , 分别在 , 上,且 , 与相交于点 . (1)、求证:≌;(2)、求的大小.19. 如图,的对角线、相交于点 . 求证:是菱形.
(1)、求证:≌;(2)、求的大小.19. 如图,的对角线、相交于点 . 求证:是菱形.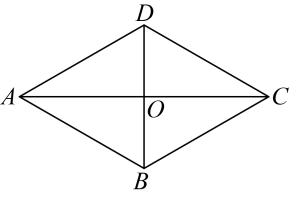 20. 如图,在中,D是的中点,E是的中点,过点A作交的延长线于点F.
20. 如图,在中,D是的中点,E是的中点,过点A作交的延长线于点F.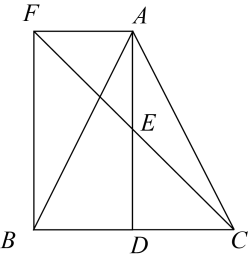 (1)、求证:;(2)、连接 , 若 , 求证:四边形是矩形.21. 如图,和相交于点 , , . 点、分别是、的中点.
(1)、求证:;(2)、连接 , 若 , 求证:四边形是矩形.21. 如图,和相交于点 , , . 点、分别是、的中点. (1)、求证:;(2)、当时,求证:四边形是矩形.22. 阅读与思考
(1)、求证:;(2)、当时,求证:四边形是矩形.22. 阅读与思考下面是小宣同学数学笔记中的部分内容,请认真阅读并完成相应的任务,
双关联线段
【概念理解】
如果两条线段所在直线形成的央角中有一个角是60°,且这两条线段相等,则称其中一条线段是另一条线段的双关联线段,也称这两条线段互为双关联线段。
例如,下列各图中的线段AB与CD所在直线形成的夹角中有一个角是60°,若AB=CD,则下列各图中的线段CD都是相应线段AB的双关联线段。

【问题解决】
问题1:如图1,在矩形ABCD中,AB<AD,若对角线AC与BD互为双关联线段,则∠ACB= ▲ °

问题2:如图2,在等边△ABC中,点D,E分别在边BC,CA的延长线上,且AE=CD,连接AD,BE.

求证:线段AD是线段BE的双关联线段。
证明:延长DA交BE于点F
∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60° .
∵∠BAC+∠BAE=180°,∠ACB+∠ACD=180°,
∴∠BAE=ㄥACD(依据).
∵AE=CD, ∴△ABE≌△CAD.
∴BE=AD,∠E=∠D.
任务:
(1)、问题1 中的∠ACB=°,问题2中的依据是.
(2)、补全问题2的证明过程;(3)、如图3,点C在线段AB上,请在图3中作线段AB的双关联线段CD(要求:①尺规作图,保留作图痕迹,不写作法;②作出一条即可).
 23. 【问题解决】
23. 【问题解决】如图①,在矩形ABCD中,点E,F分别在边AB,BC上,DE=AF,DE⊥AF 于点G.
(1)、求证:四边形ABCD 是正方形.(2)、延长CB 到点 H,使得BH=AE,判断△AHF 的形状,并说明理由.(3)、【类比迁移】如图②,在菱形ABCD 中,点E,F 分别在边AB,BC上,DE 与AF 相交于点G,DE=AF,∠AED=60°,AE=6,BF=2,求 DE 的长.
24. 在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC 与DEF 拼在一起,使点A 与点F 重合,点C与点D 重合(如图①),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4 cm,并进行如下研究活动.
活动一:将图①中的纸片DEF 沿AC 方向平移,连接AE,BD(如图②),当点 F 与点C 重合时停止平移.
(1)、【思考】图②中的四边形ABDE 是平行四边形吗?请说明理由.(2)、【发现】当纸片DEF 平移到某一位置时,小兵发现四边形 ABDE 为矩形(如图③),求AF 的长.活动二:在图③中,取AD 的中点O,再将纸片DEF 绕点O顺时针方向旋转α度(0≤α≤90),连接OB,OE(如图④).(3)、【探究】当 EF 平分∠AEO时,探究OF 与BD 的数量关系,并说明理由.