浙江省杭州市上城区2024-2025学年下学期七年级期末考试数学试卷
试卷更新日期:2025-07-28 类型:期末考试
一、选择题:本大题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 如图所示的图案可以看作由“基本图案”经过平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列数据收集过程中,适合用普查的是( )A、五一期间来杭游客最喜爱的景点调查 B、神舟二十号发射前火箭零部件检查 C、全市学生对学校食堂满意度调查 D、某农场小麦种子单穗颗粒数调查3. 下列多项式,能用平方差公式进行因式分解的是( )A、 B、 C、 D、4. 如图所示,下列说法不正确的是
2. 下列数据收集过程中,适合用普查的是( )A、五一期间来杭游客最喜爱的景点调查 B、神舟二十号发射前火箭零部件检查 C、全市学生对学校食堂满意度调查 D、某农场小麦种子单穗颗粒数调查3. 下列多项式,能用平方差公式进行因式分解的是( )A、 B、 C、 D、4. 如图所示,下列说法不正确的是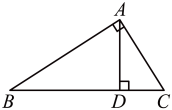 A、线段BD是点B到AD的垂线段 B、线段AD是点D到BC的垂线段 C、点C到AB的垂线段是线段AC D、点B到AC的垂线段是线段AB5. 下列运算中,结果正确的是( )A、 B、 C、 D、6. 如图,下列说法正确的是( )
A、线段BD是点B到AD的垂线段 B、线段AD是点D到BC的垂线段 C、点C到AB的垂线段是线段AC D、点B到AC的垂线段是线段AB5. 下列运算中,结果正确的是( )A、 B、 C、 D、6. 如图,下列说法正确的是( )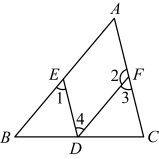 A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 下列各式从左到右的变形中,正确的是( )A、 B、 C、 D、8. 2025杭州钱塘女子半程马拉松在钱塘区6号大街鸣枪开跑.小江、小周参加千米的迷你马拉松比赛,两人约定从A地沿相同路线跑向距A地千米的B地.已知小江跑步的速度是小周的倍.若两人同时从A地出发,结果小江到达B地分钟后小周才到达.设小周跑步的速度为每小时x千米,则可列方程( )A、 B、 C、 D、9. 如图,在周长为60的长方形中放入6个相同的小长方形,若小长方形面积为S , 长为x , 宽为 , 则( )
A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 下列各式从左到右的变形中,正确的是( )A、 B、 C、 D、8. 2025杭州钱塘女子半程马拉松在钱塘区6号大街鸣枪开跑.小江、小周参加千米的迷你马拉松比赛,两人约定从A地沿相同路线跑向距A地千米的B地.已知小江跑步的速度是小周的倍.若两人同时从A地出发,结果小江到达B地分钟后小周才到达.设小周跑步的速度为每小时x千米,则可列方程( )A、 B、 C、 D、9. 如图,在周长为60的长方形中放入6个相同的小长方形,若小长方形面积为S , 长为x , 宽为 , 则( )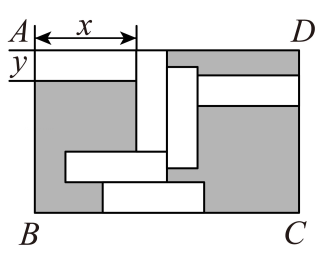 A、若 , 则 B、若 , 则 C、若 , 则 D、若为整数,则10. 已知 , , , 下列计算结果正确的是( )
A、若 , 则 B、若 , 则 C、若 , 则 D、若为整数,则10. 已知 , , , 下列计算结果正确的是( )①;②;③;④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题:本大题有6个小题,每小题3分,共18分.
-
11. 写一个解为的二元一次方程 .12. 分解因式:x2y-4y= .13. 2025年春节期间,杭州科技领域引发热议,其中人工智能“”火爆全网,在“”中字母“E”的出现频率是 .14. 如图, , 将一个含角的直角三角板如图放置,使点E落在直线上,若 , 则的度数为 .
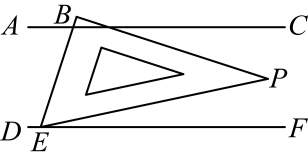 15. 在公式中,将这个公式变形为已知 , 求b的公式: .16. 四张正方形纸片如图放置,使得三点共线.设正方形 , 正方形的面积分别为 .
15. 在公式中,将这个公式变形为已知 , 求b的公式: .16. 四张正方形纸片如图放置,使得三点共线.设正方形 , 正方形的面积分别为 .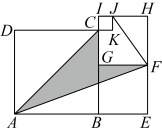
⑴若 , 则阴影部分的面积 .
⑵若阴影部分的面积与的面积差为5,则 .
三、解答题:本大题有8个小题,共72分.解答应写出文字说明、证明过程或演算步骤.
-
17. 计算:(1)、(2)、18. 为响应国家人工智能赋能教育政策,增强学生数智素养,某学校开展“学伴”计划.为了解学生对不同智能大模型的使用情况,在七、八、九三个年级随机抽取了若干名学生,对他们最喜爱使用的一种人工智能软件(每人只选一项)进行了问卷调查,将数据统计后,绘制出两幅不完整的统计图,其中深度求索,通义千问,豆包,讯飞星火,其他 . 根据图1,图2中的信息,解答下列问题:
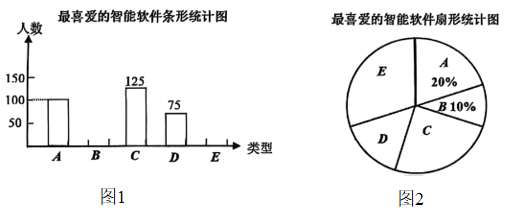 (1)、这次调查中接受问卷调查的同学共有名;(2)、补全条形统计图;(3)、根据统计结果,若该校有200名学生选择B类,请估计该校选择C类学生人数.19. 解方程(组)(1)、(2)、20. 先化简再求值: , 其中 .21. 已知:如图,在中, , 点分别在上,且平分 , .
(1)、这次调查中接受问卷调查的同学共有名;(2)、补全条形统计图;(3)、根据统计结果,若该校有200名学生选择B类,请估计该校选择C类学生人数.19. 解方程(组)(1)、(2)、20. 先化简再求值: , 其中 .21. 已知:如图,在中, , 点分别在上,且平分 , .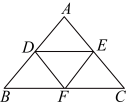 (1)、判断与的位置关系,并说明理由.(2)、若 , 求的度数.22. 对于关于x的四个多项式(是常数),任意两个多项式的积与另外两个多项式的积的差,若其中一种组合得到结果为常数n , 称这种组合为消元组合,常数n是这种组合的消元余量.
(1)、判断与的位置关系,并说明理由.(2)、若 , 求的度数.22. 对于关于x的四个多项式(是常数),任意两个多项式的积与另外两个多项式的积的差,若其中一种组合得到结果为常数n , 称这种组合为消元组合,常数n是这种组合的消元余量.例如:对于多项式 ,
因为
所以这种组合为消元组合,其消元余量为 .
因为 , 结果不是常数;
所以这种组合不是消元组合.
(1)、若多项式 , 判断是否为消元组合,若是,请求出消元余量,若不是,请说明理由.(2)、若多项式存在消元组合,则p的值为 .(3)、若多项式存在消元组合,求a与b的关系式.23. 某水果店销售苹果单价8元/千克,梨单价6元/千克.(1)、小明购买了苹果和梨,共支付44元,其中苹果比梨多买了2千克,求小明购买的苹果和梨的重量;(2)、水果店推出一种苹果与梨搭配销售方式,若搭配方式由苹果a千克,梨b千克组成,则苹果单价下降元/千克,梨单价上涨m元/千克.①请用含的代数式表示搭配销售方式水果平均单价 ▲ .
②按搭配销售方式购买后,发现无论m为何值,支付的金额始终与小明相同,求搭配销售方式中苹果的重量a的值.
24. 如图1, , 点E在上,点H在上,点F在直线之间,连接 .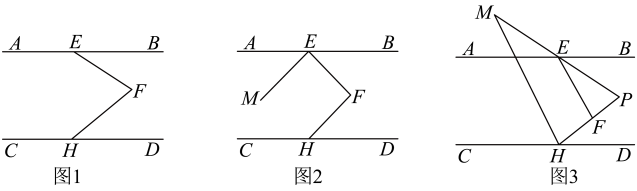 (1)、求证: .(2)、如图2,点M在直线与之间,且 , 若 , 求的度数.(3)、如图3,连结 , 移动点M至直线上方,使得 , 延长交直线于点P , 若(n为整数且),求的值(用含n的代数式表示).
(1)、求证: .(2)、如图2,点M在直线与之间,且 , 若 , 求的度数.(3)、如图3,连结 , 移动点M至直线上方,使得 , 延长交直线于点P , 若(n为整数且),求的值(用含n的代数式表示).