浙江省金华市金东区2024-2025学年下学期八年级数学期末试题卷
试卷更新日期:2025-07-28 类型:期末考试
一、选择题(本题有10小题,每小题3分,共30分.)
-
1. 硼、碳、氧、氟是化学元素周期表中第二周期的四种元素,下列选项中分别是它们的元素符号,其中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算中正确的是( )A、 B、 C、 D、3. 抛物线与y轴的交点坐标为( )A、 B、 C、 D、4. 在 22,24,27,22,25,22 中插入一个任意数 x,则一定不会改变的是( )A、平均数 B、众数 C、中位数 D、方差5. 如图是一枚2025年发行的正十二边形纪念币(每个内角相等),则该正十二边形的每个内角为( )
2. 下列计算中正确的是( )A、 B、 C、 D、3. 抛物线与y轴的交点坐标为( )A、 B、 C、 D、4. 在 22,24,27,22,25,22 中插入一个任意数 x,则一定不会改变的是( )A、平均数 B、众数 C、中位数 D、方差5. 如图是一枚2025年发行的正十二边形纪念币(每个内角相等),则该正十二边形的每个内角为( ) A、150° B、145° C、140° D、135°6. 已知关于x的一元二次方程的两个实数根相等,则a的值为( )A、0 B、1 C、2 D、0或27. 小琦在复习几种特殊四边形的关系时整理出如图所示的转换图,(1)(2)(3)(4)处需要添加条件,则下列条件添加错误的是( )
A、150° B、145° C、140° D、135°6. 已知关于x的一元二次方程的两个实数根相等,则a的值为( )A、0 B、1 C、2 D、0或27. 小琦在复习几种特殊四边形的关系时整理出如图所示的转换图,(1)(2)(3)(4)处需要添加条件,则下列条件添加错误的是( ) A、(1)处可填 B、(2)处可填 C、(3)处可填 D、(4)处可填8. 已知点和点均在反比例函数 (k是常数, )的图象上,下列结论正确的是( )A、当时, B、当时, C、当时, D、当时,9. 在一块矩形铁皮上裁去一个小矩形得到了如图所示的直角铁皮.用一条直线 l 将该直角铁皮分成面积相等的两部分,则符合条件的直线 l 有( )
A、(1)处可填 B、(2)处可填 C、(3)处可填 D、(4)处可填8. 已知点和点均在反比例函数 (k是常数, )的图象上,下列结论正确的是( )A、当时, B、当时, C、当时, D、当时,9. 在一块矩形铁皮上裁去一个小矩形得到了如图所示的直角铁皮.用一条直线 l 将该直角铁皮分成面积相等的两部分,则符合条件的直线 l 有( )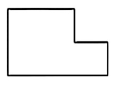 A、2 条 B、3 条 C、4 条 D、无数条10. 如图,在中, , 在上取点 , 使 , 连结 , 过点作交 , 分别于点 , . 已知 , , , 当 , 发生变化时,下列代数式值不变的是( )
A、2 条 B、3 条 C、4 条 D、无数条10. 如图,在中, , 在上取点 , 使 , 连结 , 过点作交 , 分别于点 , . 已知 , , , 当 , 发生变化时,下列代数式值不变的是( )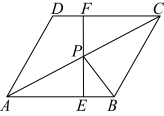 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每小题3分,共18分.)
-
11. 在二次根式中,x的取值范围是.12. 用反证法证明“已知的三边长为 , , , 若 , 则不是直角三角形”时,应先假设 .13. 若一组数据 3,5,7,x,11 的平均数为 7,则 =.14. 如图,在正方形ABCD的外侧,作等边三角形CDE,连接AE,BE,则∠AEB的度数为度.
 15. 如图,在中, , , , 于点 , 点、分别是、的中点,则的周长为 .
15. 如图,在中, , , , 于点 , 点、分别是、的中点,则的周长为 .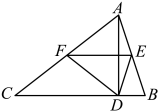 16. 如图,在矩形中,对角线 , 交于点 , 的平分线交于点 , 连结 . 已知 , , 则 .
16. 如图,在矩形中,对角线 , 交于点 , 的平分线交于点 , 连结 . 已知 , , 则 .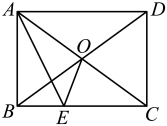
三、解答题(本题有8小题,共72分,各小题都必须写出解答过程.)
-
17. 计算: .18. 习题课上,数学老师展示嘉嘉解题的错误解答过程:
嘉嘉:解方程
解:方程两边同时除以得
第一步
第二步
第三步
(1)、嘉嘉的解答过程从第步开始出现错误的;(2)、请给出这道题的正确解答过程.19. 在中, , 点D是AB的中点.尺规作图:在BC上确定点E,连结DE,使得.现有甲、乙、丙三位同学的做法如下: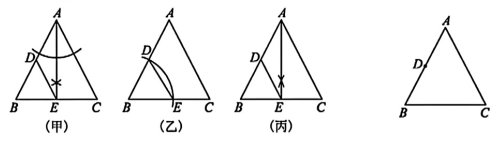 (1)、 做法正确的同学有.(2)、 用尺规作图的方法画出一种不同于以上三位同学的画法.20. 近日,深度求索推出了“DeepSeek”AI聊天机器人(以下简称A款),抖音推出了“豆包”AI聊天机器人(以下简称B款).有关人员开展了A , B两款AI聊天机器人的使用满意度评分测验,并从中各随机抽取20份,下面给出了部分信息:(单位:分)(评分分数用表示,分为四个等级:不满意 , 比较满意 , 满意 , 非常满意)
(1)、 做法正确的同学有.(2)、 用尺规作图的方法画出一种不同于以上三位同学的画法.20. 近日,深度求索推出了“DeepSeek”AI聊天机器人(以下简称A款),抖音推出了“豆包”AI聊天机器人(以下简称B款).有关人员开展了A , B两款AI聊天机器人的使用满意度评分测验,并从中各随机抽取20份,下面给出了部分信息:(单位:分)(评分分数用表示,分为四个等级:不满意 , 比较满意 , 满意 , 非常满意)抽取的对A款AI聊天机器人的评分数据中“满意”的数据:83,85,86,87,88,89;
抽取的对B款AI聊天机器人的评分数据:67,68,69,83,85,86,87,87,87,88,88,89,95,96,96,96,96,98,99,100;

抽取的对A , B款AI聊天机器人的评分统计表
设备
平均数
中位数
众数
“非常满意”所占百分比
A
88
88.5
98
B
88
(1)、求出上述图表中 , , 的值;(2)、若你是用户,从平均数、中位数、众数的这三个角度进行分析,你认为哪款聊天机器人更受喜爱?请说明理由.21. 在平面直角坐标系中,一次函数的图象与反比例函数的图象交于两点.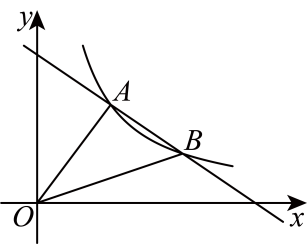 (1)、求反比例函数和一次函数的表达式;(2)、连接 , 求的面积.22. 随着全球对环境保护的重视,新能源汽车行业迎来了快速发展.某新能源汽车销售公司统计显示,今年三月份与五月份的新能源汽车销量分别为 4000 辆和 4840 辆,假设该公司每月新能源汽车销量的增长率相同.(1)、 求该公司新能源汽车销量的月平均增长率.(2)、 已知每辆新能源汽车的交付需要经过检测和调试等多个环节,每位员工每月可处理 250 辆汽车的交付任务.若该公司现有 20 名负责交付的员工,按(1)中的增长率预测能否完成今年六月份的新能源汽车交付任务?若不能,至少需要增加几名员工.23. 二次函数的图象经过点 , 且对称轴为直线 .(1)、求这个二次函数的解析式.(2)、若一个点的坐标满足 , 我们将这样的点定义为“倍值点”.
(1)、求反比例函数和一次函数的表达式;(2)、连接 , 求的面积.22. 随着全球对环境保护的重视,新能源汽车行业迎来了快速发展.某新能源汽车销售公司统计显示,今年三月份与五月份的新能源汽车销量分别为 4000 辆和 4840 辆,假设该公司每月新能源汽车销量的增长率相同.(1)、 求该公司新能源汽车销量的月平均增长率.(2)、 已知每辆新能源汽车的交付需要经过检测和调试等多个环节,每位员工每月可处理 250 辆汽车的交付任务.若该公司现有 20 名负责交付的员工,按(1)中的增长率预测能否完成今年六月份的新能源汽车交付任务?若不能,至少需要增加几名员工.23. 二次函数的图象经过点 , 且对称轴为直线 .(1)、求这个二次函数的解析式.(2)、若一个点的坐标满足 , 我们将这样的点定义为“倍值点”.①求这个函数“倍值点”的坐标;
②若是该二次函数图象上“倍值点”之间的点(包括端点),求的最大值与最小值的差.
24. 如图,在菱形ABCD中,对角线AC与BD相交于点O,在CD上取点E,连接AE,将沿AE折叠,点D的对应点为F.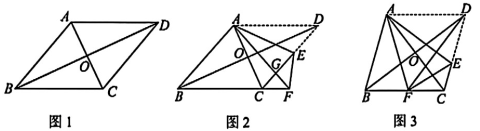 (1)、如图1,若 , , 求菱形ABCD的面积.(2)、如图2,若点F落在BC的延长线上,求证:.(3)、如图3,若点F落在BC上,连接DF,已知 ,
(1)、如图1,若 , , 求菱形ABCD的面积.(2)、如图2,若点F落在BC的延长线上,求证:.(3)、如图3,若点F落在BC上,连接DF,已知 ,① 求DF的长;
② 直接写出四边形ADEF的面积.