浙江省丽水市莲都区2024-2025学年七年级下学期期末数学试题
试卷更新日期:2025-07-28 类型:期末考试
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 计算的结果是( )A、2025 B、1 C、0 D、2. 下列方程中是二元一次方程的是( )A、 B、 C、 D、3. 人体一根头发的直径约为米,将数字用科学记数法表示为( )A、 B、 C、 D、4. 若分式的值为零,则的值是( )A、 B、 C、 D、5. 下列等式从左边到右边的变形,属于因式分解的是( )A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 我校在一次歌唱选拔比赛中,将所有参赛学生的成绩绘制成如图所示的折线统计图,则下列说法错误的是( )
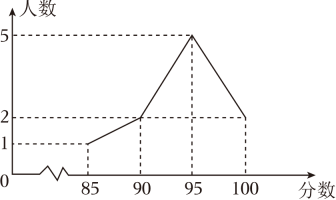 A、最高分为100分 B、最高分与最低分的差是15分 C、参赛学生人数为8人 D、参赛学生的满分率为8. 若展开后不含的项,则m的值是( )A、 B、1 C、3 D、9. 为解决供水问题需铺设一条长2400米的管道,实际施工时…….设实际每天铺设管道米,可得方程 . 根据此情景,题中用“……”表示的缺失条件为( ).A、每天比原计划少铺设20米,结果延期6天完成 B、每天比原计划多铺设20米,结果提前6天完成 C、每天比原计划少铺设6米,结果延期20天完成 D、每天比原计划多铺设6米,结果提前20天完成10. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与另一束经过光心的光线相交于点 , 点为焦点.若 , 则的度数表示为( )
A、最高分为100分 B、最高分与最低分的差是15分 C、参赛学生人数为8人 D、参赛学生的满分率为8. 若展开后不含的项,则m的值是( )A、 B、1 C、3 D、9. 为解决供水问题需铺设一条长2400米的管道,实际施工时…….设实际每天铺设管道米,可得方程 . 根据此情景,题中用“……”表示的缺失条件为( ).A、每天比原计划少铺设20米,结果延期6天完成 B、每天比原计划多铺设20米,结果提前6天完成 C、每天比原计划少铺设6米,结果延期20天完成 D、每天比原计划多铺设6米,结果提前20天完成10. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与另一束经过光心的光线相交于点 , 点为焦点.若 , 则的度数表示为( )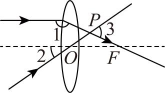 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每小题3分,共18分)
-
11. 因式分解: .12. 将变形,用含的代数式表示 , 那么 .13. 如图,将三角形沿方向平移到三角形的位置,已知点之间的距离为1, , 则的长是 .
 14. 一次数学测试后,某班50名学生的成绩被分为5组,第1至4组的频数分别为13、9、8、10,则第5组的频率是 .15. 规定:若实数满足(且),则记作 . 例如: , 则 . 若 , 且 , 则的值是 .16. 如图,正方形 , 正方形和正方形摆放在长方形中, , 且 . 已知正方形与正方形的面积之和为7,则长方形的面积为 .
14. 一次数学测试后,某班50名学生的成绩被分为5组,第1至4组的频数分别为13、9、8、10,则第5组的频率是 .15. 规定:若实数满足(且),则记作 . 例如: , 则 . 若 , 且 , 则的值是 .16. 如图,正方形 , 正方形和正方形摆放在长方形中, , 且 . 已知正方形与正方形的面积之和为7,则长方形的面积为 .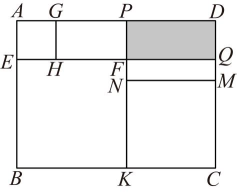
三、解答题(本题有8小题,第17~21题每题8分,第22,23题每题10分,第24题12分,共72分,各小题都必须写出解答过程)
-
17.(1)、计算:(2)、化简:18. 解方程(组)(1)、(2)、19. 先化简,再求值: , 其中 .20. 某中学数学兴趣小组在开展主题为“绿色出行从我做起——学生上学方式”的调查活动,采取随机抽样的方式进行问卷调查,问卷调查结果分为“私家车接送”“乘公交车”“骑自行车”“步行”四种上学方式,数据整理如下表.
上学方式
私家车接送
乘公交车
步行
骑自行车
频数
54
92
12
42
频率
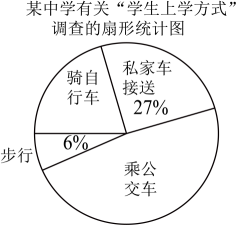 (1)、本次问卷调查取样的样本容量为 , 表中的值为 .(2)、根据表中数据计算“骑自行车”上学的频数在扇形统计图中所对应扇形的圆心角的度数.(3)、若该中学有1500人,根据调查结果估计全校学生中“乘公交车”上学的人数.21. 如图,是内一点,点在上.过点画一条直线平行于 , 过点画一条直线平行于 , 直线交于 .
(1)、本次问卷调查取样的样本容量为 , 表中的值为 .(2)、根据表中数据计算“骑自行车”上学的频数在扇形统计图中所对应扇形的圆心角的度数.(3)、若该中学有1500人,根据调查结果估计全校学生中“乘公交车”上学的人数.21. 如图,是内一点,点在上.过点画一条直线平行于 , 过点画一条直线平行于 , 直线交于 .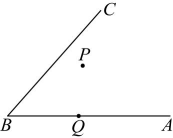 (1)、用直尺和三角尺画平行线的方法,画出图形.(2)、若 , 求的度数.22. 已知 .(1)、当时,求的值.(2)、试说明无论取何值时, .23. 根据以下素材,探索完成任务.
(1)、用直尺和三角尺画平行线的方法,画出图形.(2)、若 , 求的度数.22. 已知 .(1)、当时,求的值.(2)、试说明无论取何值时, .23. 根据以下素材,探索完成任务.如何设计门票购买方案?
素材1
乒乓球比赛的门票分为三个档次,购买1张档门票和2张档门票需要700元;购买2张档门票和3张档门票需要1200元;购买1张档门票需要80元.
素材2
购票平台有优惠活动:每购买1张A档门票就赠送1张C档门票.
素材3
某公司计划组织30名员工观看比赛.

问题解决
任务1
求档和档门票的单价.
任务2
购买门票中,档9张,档11张,求公司购买门票至少需要多少元.
任务3
该公司购买门票共花了4040元,且赠送的档门票全部用完.请你求出所有符合条件的购买方案,并写出解答过程.
24. 如图,将两个直角三角尺作如下摆放, , 直线过点 , 在直线上,平分 .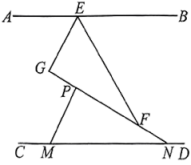 (1)、求的度数.(2)、试判断与的位置关系,并说明理由.(3)、将绕点逆时针旋转,速度为每秒 , 同时绕点逆时针旋转,速度为每秒 , 记旋转时间为 , 当旋转一周时,整个运动停止.当与的任意一边平行时,求出所有满足条件的的值.
(1)、求的度数.(2)、试判断与的位置关系,并说明理由.(3)、将绕点逆时针旋转,速度为每秒 , 同时绕点逆时针旋转,速度为每秒 , 记旋转时间为 , 当旋转一周时,整个运动停止.当与的任意一边平行时,求出所有满足条件的的值.