浙江省湖州市德清县2024-2025学年下学期七年级期末测试数学试卷
试卷更新日期:2025-07-28 类型:期末考试
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 下列方程中,属于二元一次方程的是( )A、 B、 C、 D、2. 2024年4月,北京大学团队研发出全球最薄的光学晶体-转角菱方氮化硼光学晶体,其厚度仅为米,能效比传统晶体提升了100至1万倍,数据用科学记数法表示为( )A、 B、 C、 D、3. 如图,与是同旁内角的是( )
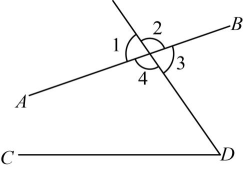 A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 下列调查中,适合用抽样调查方式的是( )A、了解七年级(1)班学生每周的体育锻炼时长 B、旅客登飞机前的安检 C、日光灯管厂要检测一批灯管的使用寿命 D、某公司职工进行健康检查6. 把分式的分子分母中的a , b都扩大为原来的2倍,则分式的值( )A、不变 B、扩大为原来的2倍 C、缩小为原来的 D、缩小为原来的7. 如果 , 那么m的值不能取( )A、0 B、1 C、2 D、48. 《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木头的长,绳子还剩余尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为x尺,绳子长为y尺,则所列方程组正确的是( )A、 B、 C、 D、9. 小明在数学课堂折纸活动中,将一张长方形纸片沿着翻折,点A , D的对应点分别为 , , 与交于点G , 再将沿着边翻折,点的对应点落在长方形的内部点H处,若平分 , 则的度数为( )
A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 下列调查中,适合用抽样调查方式的是( )A、了解七年级(1)班学生每周的体育锻炼时长 B、旅客登飞机前的安检 C、日光灯管厂要检测一批灯管的使用寿命 D、某公司职工进行健康检查6. 把分式的分子分母中的a , b都扩大为原来的2倍,则分式的值( )A、不变 B、扩大为原来的2倍 C、缩小为原来的 D、缩小为原来的7. 如果 , 那么m的值不能取( )A、0 B、1 C、2 D、48. 《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木头的长,绳子还剩余尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为x尺,绳子长为y尺,则所列方程组正确的是( )A、 B、 C、 D、9. 小明在数学课堂折纸活动中,将一张长方形纸片沿着翻折,点A , D的对应点分别为 , , 与交于点G , 再将沿着边翻折,点的对应点落在长方形的内部点H处,若平分 , 则的度数为( )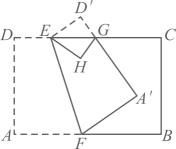 A、 B、 C、 D、10. 如图,已知正方形与正方形的重叠部分是长方形 , 面积记为 , 四边形与四边形都为正方形,面积分别记为和 , 已知 , 则下列代数式的值为定值的是( )
A、 B、 C、 D、10. 如图,已知正方形与正方形的重叠部分是长方形 , 面积记为 , 四边形与四边形都为正方形,面积分别记为和 , 已知 , 则下列代数式的值为定值的是( )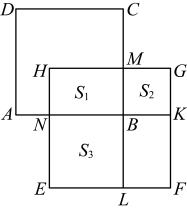 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每小题3分,共18分)
-
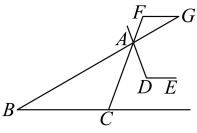
11. 计算:12. 当时,分式无意义.13. 已知在一个样本中,50个数据分别落在5个组内,第一、二、三、五组数据的频数分别为2,8,15,5,则第四组数据的频率是 .14. 若实数a , b满足 , , 则的值是 .15. 若满足 , 则 .16. 如图,小盟利用几何图形画出螳螂简笔画, , 交于点 , , , 平分 , 若 , 则的度数为 .
三、解答题(本题有8小题,共72分)
-
17. 因式分解(1)、(2)、18. 解方程(组)(1)、(2)、19. 化简: , 再在1,0,三个数中选择适当的数为x的值代入求值.20. 某工厂设计了一个新的零件模型,该模型平面图为一个大长方形,内部挖去两个相同的小长方形(如图).其中大长方形的长为 , 宽为 , 每个小长方形的长为 , 宽为 .
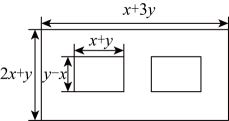 (1)、用含x , y的代数式表示该零件模型的面积并化简;(2)、当 , 时,求该零件模型的面积.21. 某地区随机抽取部分七年级学生长跑项目的达标测试成绩,成绩记为分,分,分,分四个等级,将结果绘制成如下条形统计图和扇形统计图,根据图中信息,回答下列问题:
(1)、用含x , y的代数式表示该零件模型的面积并化简;(2)、当 , 时,求该零件模型的面积.21. 某地区随机抽取部分七年级学生长跑项目的达标测试成绩,成绩记为分,分,分,分四个等级,将结果绘制成如下条形统计图和扇形统计图,根据图中信息,回答下列问题: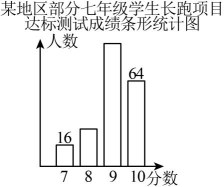
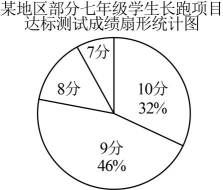 (1)、本次共抽取学生多少人?(2)、计算成绩为分的学生人数及扇形统计图中分区域的圆心角的度数;(3)、若该地区共有七年级学生约人,那么成绩为分和分的学生共有多少人?22. 如图,在直角三角形中, , , , .
(1)、本次共抽取学生多少人?(2)、计算成绩为分的学生人数及扇形统计图中分区域的圆心角的度数;(3)、若该地区共有七年级学生约人,那么成绩为分和分的学生共有多少人?22. 如图,在直角三角形中, , , , .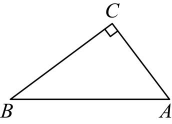 (1)、点B到的距离是;点到的距离是cm.(2)、画出表示点C到的距离的线段,并求这个距离.23. 根据以下素材,探索完成任务.
(1)、点B到的距离是;点到的距离是cm.(2)、画出表示点C到的距离的线段,并求这个距离.23. 根据以下素材,探索完成任务.学校奖品购买方案设计
素材1
某现代科技产品专卖店销售智能手环与无线耳机,已知智能手环的单价是无线耳机的1.5倍.小张发现,用1080元购买智能手环的数量比用600元购买无线耳机的数量多3件.
素材2
某学校计划花费5400元在该专卖店购买智能手环和无线耳机作为科技节奖品颁发给“科技小能手”.购买后发现,智能手环的数量比无线耳机少15只.
素材3
学校完成购买后,专卖店为了回馈学校,赠送了m张()优惠券用于下次购物抵扣.使用这些优惠券后,通过再次购买或兑换,使得智能手环与无线耳机的数量最终相同.

问题解决
任务一
【探求商品单价】请运用适当方法,求出智能手环与无线耳机的单价.
任务二
【探究购买方案】在不使用兑换券的情况下,根据学校的购买情况,求出原本购买的智能手环与无线耳机的数量.
任务三
【确定兑换方式】运用数学知识,确定兑换方案,并求出m的值.
24. 如图,直线 , 被直线所截, , 一块含角的直角三角板( , )按如图1放置,点E , F分别在直线 , 上,且 , 的平分线交直线于点H .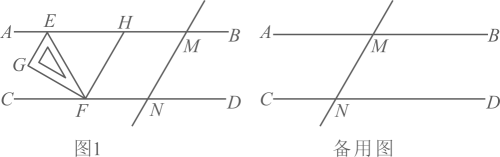 (1)、填空:(填“”,“”或“”);(2)、当时,求的度数;(3)、将三角板沿直线左右移动,并保持(点F不与点N重合),设 , 在平移的过程中求的度数(用含α的代数式表示).
(1)、填空:(填“”,“”或“”);(2)、当时,求的度数;(3)、将三角板沿直线左右移动,并保持(点F不与点N重合),设 , 在平移的过程中求的度数(用含α的代数式表示).