浙江省温州市新力量2024-2025学年高二下学期6月期末数学试题
试卷更新日期:2025-07-01 类型:期末考试
一、单项选择题:(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 已知集合 , , , 则( )A、 B、 C、 D、2. 已知向量 , , 若 , 则( )A、 B、1 C、 D、23. 已知 , 下列不等式一定成立的是( )A、 B、 C、 D、4. 生物学上,J型增长是指在理想状态下,物种迅速爆发的一种增长方式,其表达式为 , 其中为初始个体数,为最终个体数.若某种群在该模型下,个体数由100增长至120消耗了10天,则个体数由120增长至160消耗的时间大约为( )(参考数据: , )A、14 B、15 C、16 D、175. 在平行四边形中,是线段上一点, , , .若 , 则( )A、 B、 C、 D、6. 一个袋子中有完全相同的个红球,3个白球.若采取不放回方式从中随机摸出两个球,摸出的2个球都是红球的概率是.现采取放回方式从中依次摸出3个球,求恰有两次抽出红球的概率为( )A、 B、 C、 D、7. 已知一函数 , 其定义域为 , 则满足不等式的的取值范围为( )A、 B、 C、 D、8. 已知 , , 记集合 , , 若 , 则实数的取值范围为( )A、 B、 C、 D、
二、多项选择题:(本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,有错误的得0分,部分选对得部分分)
-
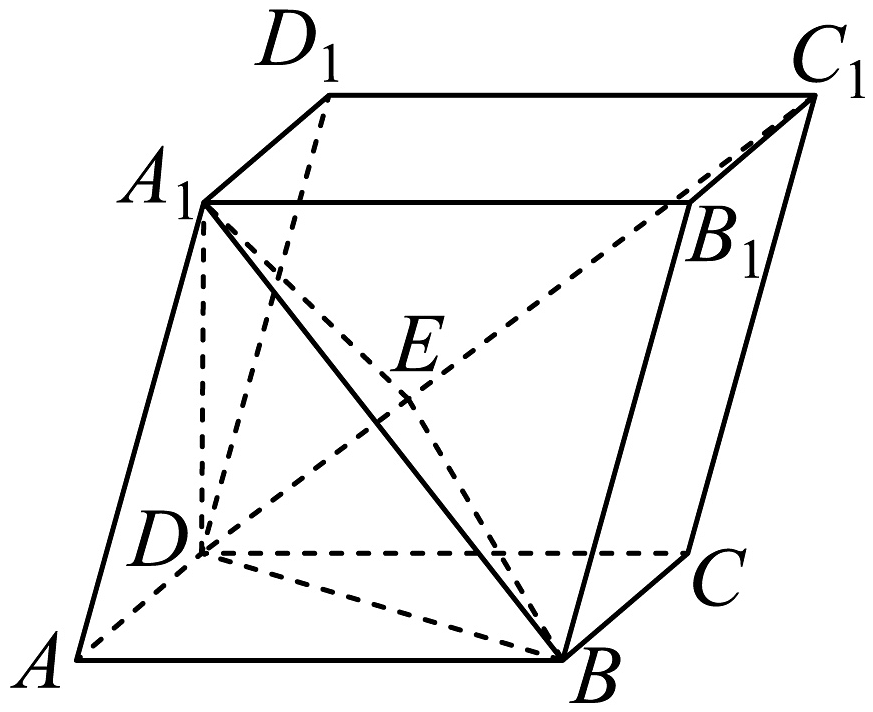
9. 已知 , 是两条不同的直线, , 是两个不同的平面,则下列命题正确的是( )A、若且 , 则 B、若 , , , 共面,则 C、若不垂直于 , 且 , 则必不垂直于 D、若且 , 则10. 已知 , , 则下列说法正确的是( )A、若 , 则的最大值为 B、的最小值为 C、若 , 则 D、若 , 则的最小值为11. 已知在正方体中, , 点为的中点,点为正方形内一点(包含边界),下列说法正确的是( )A、若点是中点,则、、、四点共面 B、存在点 , 使得直线与所成角为 C、若直线平面 , 则三棱锥的体积为定值 D、若 , 那么点的轨迹长度为
三、填空题:(本大题共3小题,每题5分,共15分)
-
12. 已知 , 则.13. 已知一底面边长为的正三棱柱有内切球,则该正三棱柱外接球的表面积为.14. 已知函数在区间内不存在零点,则的取值范围是.
四、解答题:(本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
-
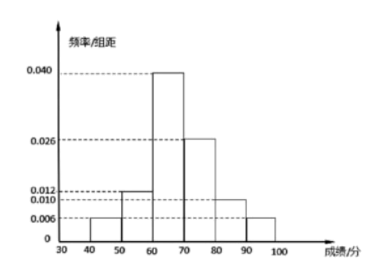
15. 已知函数.(1)、求的最小正周期和值域;(2)、先将的图象向左平移个单位,再保持纵坐标不变,横坐标缩小到原来的 , 得到的图象,求的单调递增区间.16. 已知 , , 分别为角 , , 的对边,.(1)、求;(2)、若 , , 点在边上,且是的角平分线,求.17. 为迎接新一年五四青年节,某中学举办了一次名为《回首辉煌路,做好接班人》的党团史竞赛并计划对成绩前10%的学生进行颁奖.试卷满分为100分,所有学生成绩均在区间分内.已知该校高一、高二、高三年级参加的学生人数分别为200、250、300.现用分层抽样的方法抽取了75名学生的答题成绩,绘制了如下样本频率分布直方图.
年级
样本平均数
样本方差
高一
75
75
高二
69
高三
55
(1)、根据样本频率分布直方图估计该校全体学生成绩的众数、平均数以及得奖的最低分数;(2)、已知所抽取各年级答题成绩的平均数、方差的数据如下表,且根据频率分布直方图估计出总成绩的方差为80,求高三年级学生成绩的平均数和高二年级学生成绩的方差.