广东省江门市新会第一中学2024-2025学年高二下学期期末考试数学试卷
试卷更新日期:2025-07-22 类型:期末考试
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.
-
1. 计算的值是( )A、41 B、61 C、62 D、822. 下列图中,线性相关性系数最大的是( )A、
 B、
B、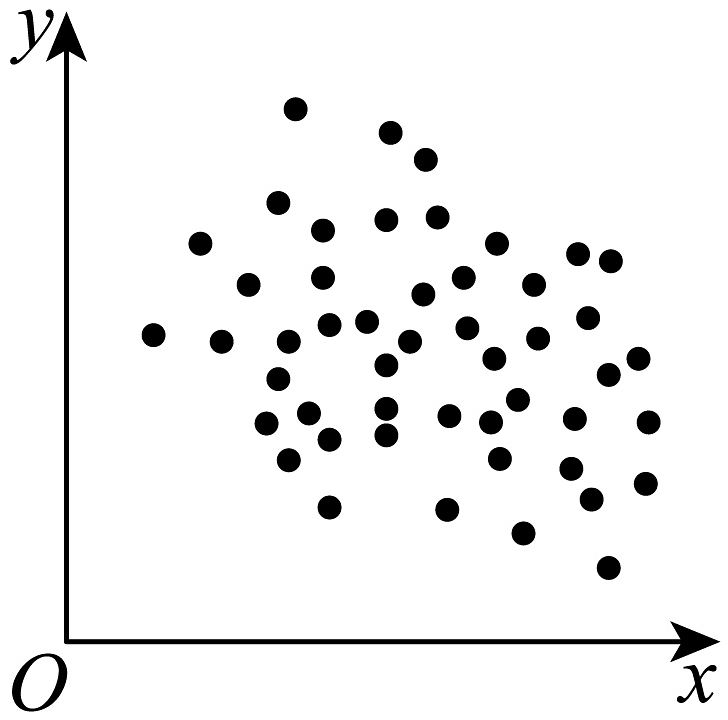 C、
C、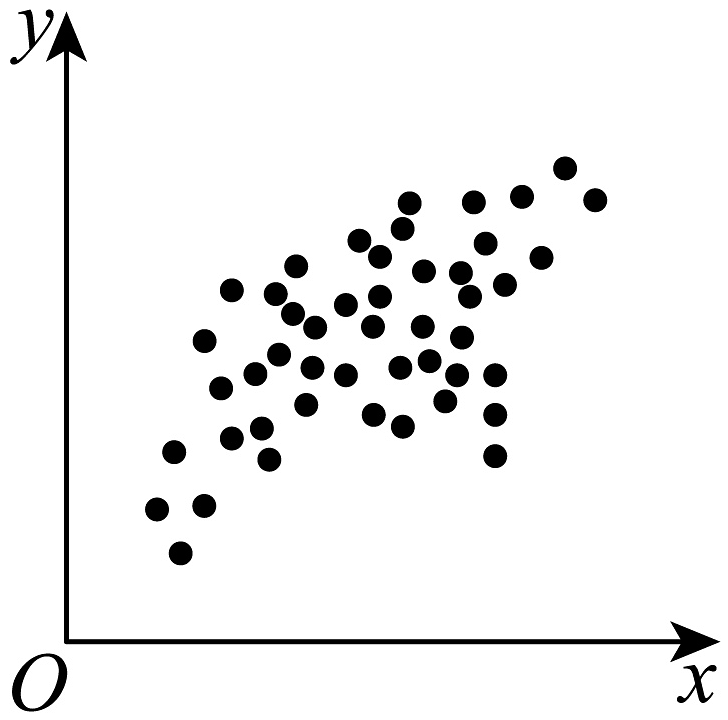 D、
D、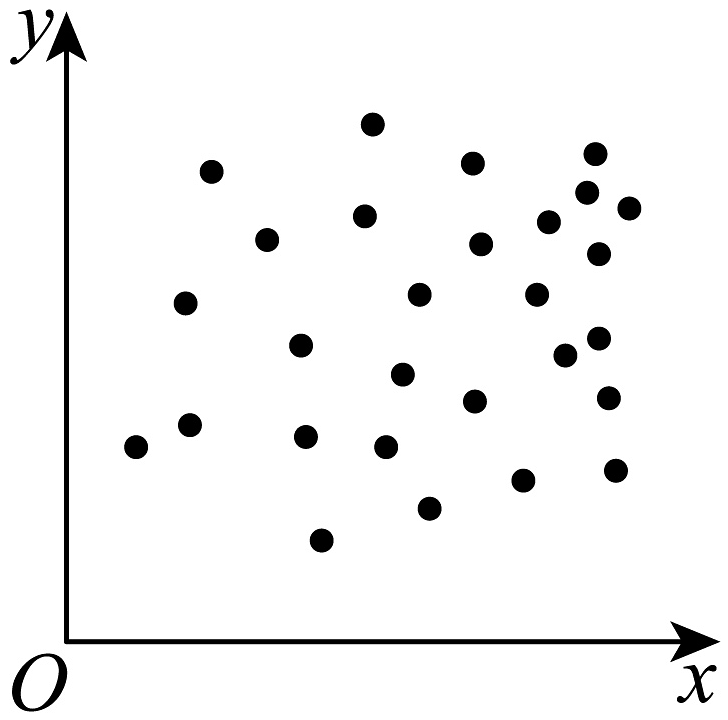 3. 记为等差数列的前n项和,已知 , , 则( )A、 B、 C、 D、4. 下列说法正确的是( )A、中国灯笼又统称为灯彩,主要有宫灯、纱灯、吊灯等种类,现有4名学生,每人从宫灯、纱灯、吊灯中选购1种,则不同的选购方式有24种 B、从A村去B村的道路有3条,从B村去C村的道路有5条,则从A村经过B村去C村不同的路线的条数为8 C、一个两层书架,分别放置语文类读物4本,数学类读物5本,每本读物各不相同,从中取出1本,则不同的取法共有20种 D、从1,2,3,4,5五个数字中任选3个数字,可组成无重复数字的三位数的个数为605. 某学校有 , 两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐.如果第1天去餐厅,那么第2天去餐厅的概率为0.6;如果第1天去餐厅,那么第2天去餐厅的概率为0.4.计算王同学第2天去餐厅用餐的概率( )A、0.24 B、0.36 C、0.5 D、0.526. 下列命题错误的是( )A、有一组数据为、、、、、、、 , 则它们的第百分位数为 B、线性回归直线一定经过样本点的中心 C、设 , 且 , 则 D、随机变量 , 若 , , 则7. 设函数 , 则曲线在点处的切线与两坐标轴所围成的三角形的面积为( )A、 B、 C、 D、8. 下列四组数据中,方差最小的为( )A、31,22,39 B、30,46,25 C、40,18,30 D、37,42,33
3. 记为等差数列的前n项和,已知 , , 则( )A、 B、 C、 D、4. 下列说法正确的是( )A、中国灯笼又统称为灯彩,主要有宫灯、纱灯、吊灯等种类,现有4名学生,每人从宫灯、纱灯、吊灯中选购1种,则不同的选购方式有24种 B、从A村去B村的道路有3条,从B村去C村的道路有5条,则从A村经过B村去C村不同的路线的条数为8 C、一个两层书架,分别放置语文类读物4本,数学类读物5本,每本读物各不相同,从中取出1本,则不同的取法共有20种 D、从1,2,3,4,5五个数字中任选3个数字,可组成无重复数字的三位数的个数为605. 某学校有 , 两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐.如果第1天去餐厅,那么第2天去餐厅的概率为0.6;如果第1天去餐厅,那么第2天去餐厅的概率为0.4.计算王同学第2天去餐厅用餐的概率( )A、0.24 B、0.36 C、0.5 D、0.526. 下列命题错误的是( )A、有一组数据为、、、、、、、 , 则它们的第百分位数为 B、线性回归直线一定经过样本点的中心 C、设 , 且 , 则 D、随机变量 , 若 , , 则7. 设函数 , 则曲线在点处的切线与两坐标轴所围成的三角形的面积为( )A、 B、 C、 D、8. 下列四组数据中,方差最小的为( )A、31,22,39 B、30,46,25 C、40,18,30 D、37,42,33二、多选题:本题共3小题,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得2分,有选错的得0分.
-
9. 下列说法正确的是( )A、利用进行独立性检验时,的值越大,说明有更大的把握认为两个分类变量独立 B、在残差图中,残差点分布的带状区域的宽度越窄,其模型拟合效果越好 C、样本相关系数r的大小可以反映成对样本数据之间线性相关的程度,当r越小,成对样本数据的线性相关程度越弱 D、用决定系数来比较两个模型的拟合效果.越大,表示残差平方和越小,即模型的拟合效果越好10. 已知离数型随机变量X的分布列如下表所示:
X
0
1
2
P
下列说法正确的是( )
A、 B、 C、 D、11. 设正整数 , 其中 , 记为上述表示中为1的个数.例如: , 所以 . 已知集合 , 下列说法正确的是( )A、 B、对任意的 , 有 C、若 , 则使成立的的取值个数为 D、三、填空题:本题共3小题,每小题5分,共15分.
-
12. 在的展开式中,的系数为 。13. 若从2025的所有正约数中任取一个数,则这个数是一个完全平方数的概率为 .14. 已知函数 , 若在处的切线斜率为 , 则;若恒成立,则的取值范围为
四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
-
15. 甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表.
机床
品级
合计
一级品
二级品
甲机床
150
50
200
乙机床
120
80
200
合计
270
130
400
(1)、甲机床、乙机床生产的产品中一级品的频率分别是多少?(2)、依据小概率值的独立性检验,分析甲机床的产品质量是否与乙机床的产品质量有差异.附:χ2=.
α
0.050
0.010
0.001
xα
3.841
6.635
10.828
16. 已知数列的前项和为 , 且(1)、求数列的通项公式;(2)、令 , 求数列的前项和17. 从2016年1月1日起全国统一实施全面两孩政策,为了解适龄民众对放开生二孩政策的态度,某市选取80后作为调查对象,随机调查了10人,其中打算生二胎的有4人,不打算生二胎的有6人.(1)、从这10人中随机抽取3人,记打算生二胎的人数为 , 求随机变量的分布列和数学期望;(2)、若以这10人的样本数据估计该市的总体数据,且以频率作为概率,从该市80后中随机抽取3人,记打算生二胎的人数为 , 求随机变量的分布列和数学期望,方差.18. 已知函数 , .(1)、当 , 时,求在区间上的最值;(2)、当时,若有三个零点 , , ,①求的取值范围;
②判断与的大小关系,并给出证明.
19. 为了治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.(1)求的分布列;
(2)若甲药、乙药在试验开始时都赋予4分,表示“甲药的累计得分为时,最终认为甲药比乙药更有效”的概率,则 , , , 其中 , , . 假设 , .
(i)证明:为等比数列;
(ii)求 , 并根据的值解释这种试验方案的合理性.