湖南省株洲市第四中学2024-2025学年高一下学期期末质量检测数学试题B
试卷更新日期:2025-07-10 类型:期末考试
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求.
-
1. 已知复数z与在复平面内对应的点关于虚轴对称,则( ).A、 B、 C、 D、2. 在中,若 , , , 则( )A、 B、 C、 D、3. 设是定义在上且周期为2的偶函数,当时, , 则( )A、 B、 C、 D、4. 如图,已知圆锥的轴截面是边长为4的正三角形,则该圆锥的侧面积为( )
 A、 B、 C、 D、5. 某项比赛共有7个评委评分,若去掉一个最高分与一个最低分,则与原始数据相比,一定不变的是( )A、极差 B、45%分位数 C、平均数 D、众数6. 我国古代数学典籍《九章算术》卷九“勾股”中有一测量问题:“今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽,问索长几何?这个问题体现了古代对直角三角形的研究,现有一竖立的木头柱子,高4米,绳索系在柱子上端,牵着绳索退行,当绳索与底面夹角为75°时绳索未用尽,再退行米绳索用尽(绳索与地面接触),则绳索长为( )A、米 B、米 C、米 D、米7. 如图,在四面体中,点在平面上的射影是 , , 若 , 则异面直线与所成角的余弦值为( )
A、 B、 C、 D、5. 某项比赛共有7个评委评分,若去掉一个最高分与一个最低分,则与原始数据相比,一定不变的是( )A、极差 B、45%分位数 C、平均数 D、众数6. 我国古代数学典籍《九章算术》卷九“勾股”中有一测量问题:“今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽,问索长几何?这个问题体现了古代对直角三角形的研究,现有一竖立的木头柱子,高4米,绳索系在柱子上端,牵着绳索退行,当绳索与底面夹角为75°时绳索未用尽,再退行米绳索用尽(绳索与地面接触),则绳索长为( )A、米 B、米 C、米 D、米7. 如图,在四面体中,点在平面上的射影是 , , 若 , 则异面直线与所成角的余弦值为( )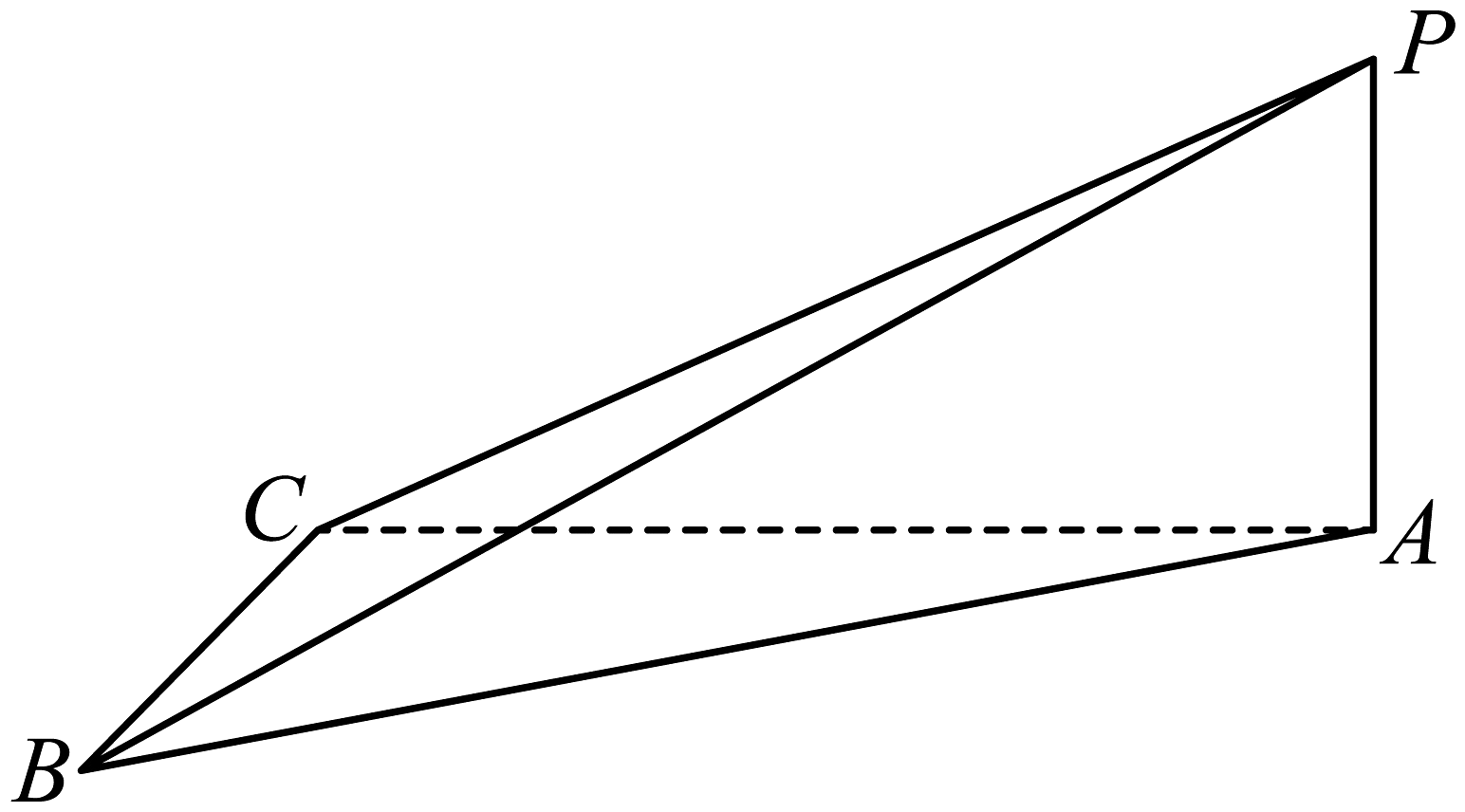 A、 B、 C、 D、8. 函数()的最大值和最小值是、 , 则的值为( )A、1 B、 C、2 D、
A、 B、 C、 D、8. 函数()的最大值和最小值是、 , 则的值为( )A、1 B、 C、2 D、二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
-
9. 已知为复数,为虚数单位,则下列结论正确的是( )A、若 , 则 B、 C、若 , 则为纯虚数 D、若 , 则的最小值为110. 连续抛掷一枚硬币两次,事件表示“第一次硬币正面朝上”,事件表示“第二次硬币反面朝上”,事件表示“两次硬币都正面朝上”,事件表示“两次硬币朝上的情况不同”,则( )A、与相互独立 B、与相互独立 C、与相互独立 D、与相互独立11. 已知正方体的棱长为2,分别是棱的中点,下列结论正确的是( )A、 B、直线与直线所成角为 C、三棱锥的体积为 D、过三点的平面截该正方体所得的截面为六边形
三、填空题:本题共3小题,每小题5分,共15分.
-
12. 若向量 , , 且 , 则.13. 一个不透明的袋中装有除颜色外均相同的9个红球,3个白球,若干个绿球,每次摇匀后随机摸出一个球,记下颜色后再放回袋中,经过大量重复实验后,发现摸到绿球的频率稳定在0.4,则袋中约有绿球个.14. 在平面四边形中, , 分别为 , 的中点,若 , , 且 , 则 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
-
15. 在中,.(1)、求的值;(2)、若 , 再从下列三个条件中选择一个作为已知,使存在,求的面积.
条件①:;条件②:;条件③:.
注:如果选择的条件不符合要求,第(Ⅱ)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
16. 如图,四棱锥的各个顶点均在球的表面上,且平面. (1)、证明:平面平面;(2)、求四棱锥体积的最大值;17. 某校数学建模社团招聘社长职位分笔试与面试两个环节,在笔试中有两轮答题:第一轮从类的5个问题中任选两题作答,若两题都答对,则得40分,否则得0分;第二轮从类的5个问题中任选两题作答,每答对1题得30分,答错得0分.若两轮总分不低于60分则进入面试环节.小红和小明参加此次招聘活动,已知小红对类每个问题的答对的概率均为0.5.在类的5个问题中,小明只能答对4个问题,在类的5个问题中,小明每个问题答对的概率都为0.4.他们回答任一问题正确与否互不影响.(1)、求小明在第一轮得40分的概率;(2)、求小红两轮总分得60分的概率;(3)、试判断小红和小明谁更有机会进入面试环节?
(1)、证明:平面平面;(2)、求四棱锥体积的最大值;17. 某校数学建模社团招聘社长职位分笔试与面试两个环节,在笔试中有两轮答题:第一轮从类的5个问题中任选两题作答,若两题都答对,则得40分,否则得0分;第二轮从类的5个问题中任选两题作答,每答对1题得30分,答错得0分.若两轮总分不低于60分则进入面试环节.小红和小明参加此次招聘活动,已知小红对类每个问题的答对的概率均为0.5.在类的5个问题中,小明只能答对4个问题,在类的5个问题中,小明每个问题答对的概率都为0.4.他们回答任一问题正确与否互不影响.(1)、求小明在第一轮得40分的概率;(2)、求小红两轮总分得60分的概率;(3)、试判断小红和小明谁更有机会进入面试环节?