浙江省宁波市奉化区2024-2025学年高一下学期期末联考数学试题+答案
试卷更新日期:2025-07-12 类型:期末考试
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
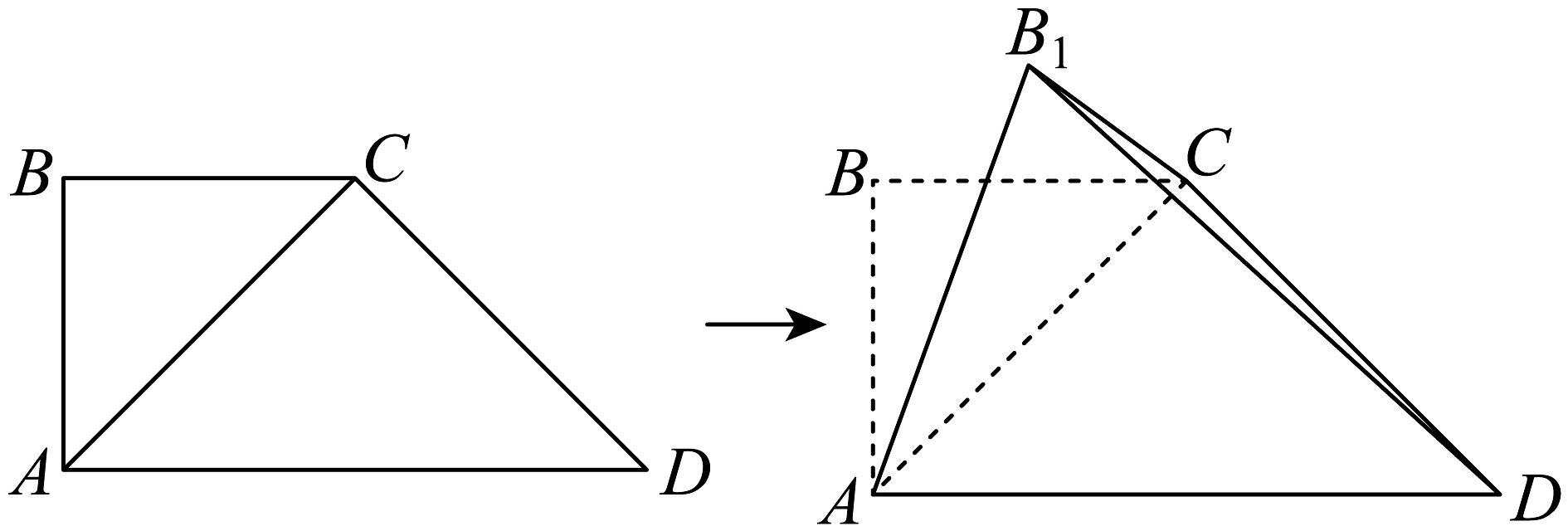
1. 若复数z满足 , 则z的虚部为( )A、1 B、 C、i D、2. 已知某平面图形的直观图是如图所示的梯形 , 且 , 则原图形OABC的面积为( )
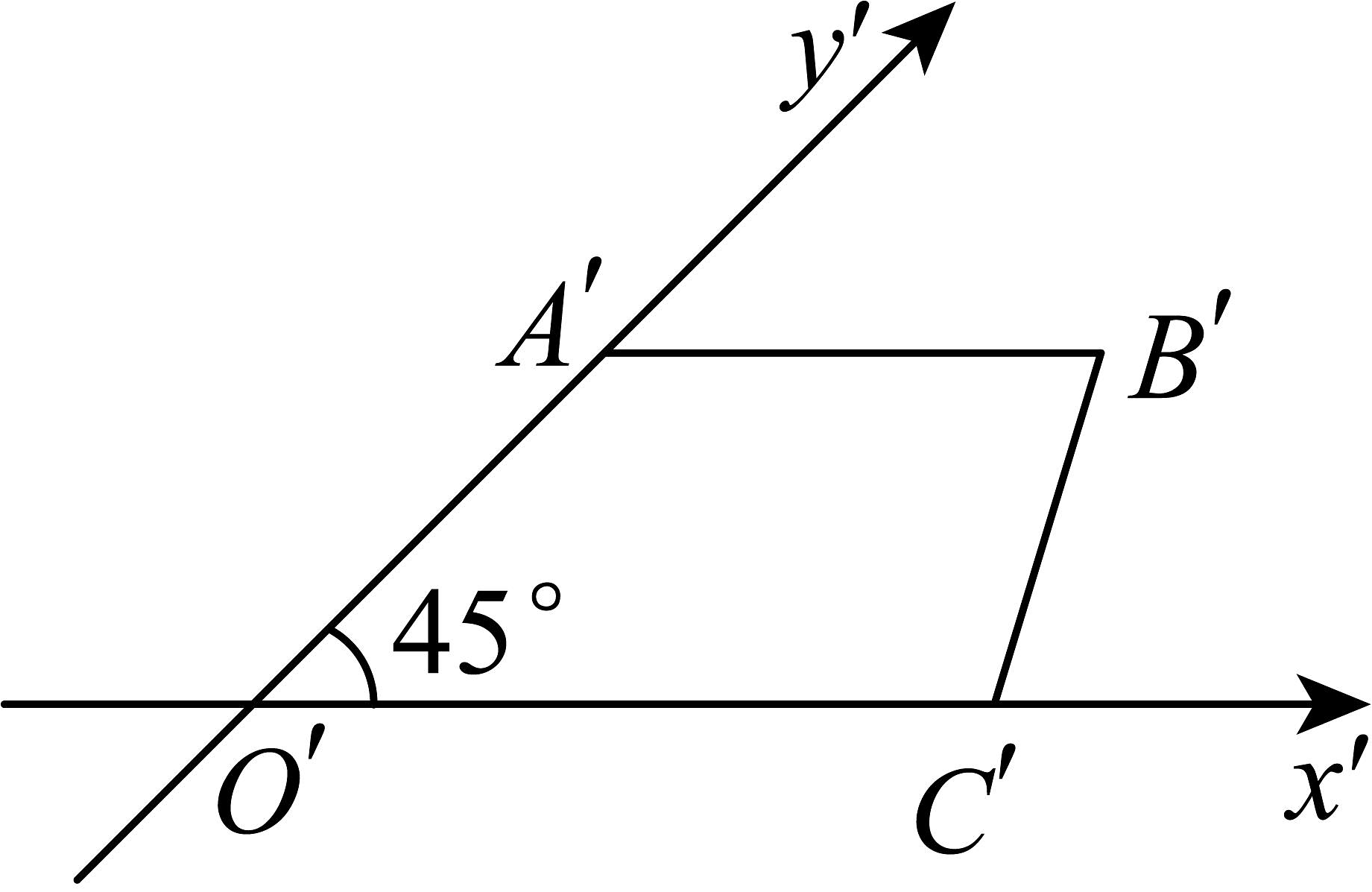 A、 B、 C、12 D、103. 已知一组数 , , , 的平均数是3,方差为4,则数据 , , , 的平均数和方差分别是( )A、7,8 B、7,16 C、6,8 D、6,164. 若 , 为空间中两条不同的直线,、为空间两个不同的平面,则下列结论不正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , , 则 D、若 , , 则5. 掷一个骰子,观察朝上的面的点数,设事件“点数为奇数”,事件“点数为的整数倍”,若 , 分别表示事件 , 发生的概率,则( )A、 , B、 , C、 D、6. 已知 , 且 , 则向量在向量上的投影向量为( )A、 B、 C、 D、7. 如图,一个底面半径为2dm,母线长为的圆锥形封闭透明容器内部装有一种液体,当圆锥底面向下平放在水平桌面上时,液面的高度恰好为圆锥的高的 , 则当圆锥的顶点在桌面上,且底面平行于水平桌面时,液面的高度为( )
A、 B、 C、12 D、103. 已知一组数 , , , 的平均数是3,方差为4,则数据 , , , 的平均数和方差分别是( )A、7,8 B、7,16 C、6,8 D、6,164. 若 , 为空间中两条不同的直线,、为空间两个不同的平面,则下列结论不正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , , 则 D、若 , , 则5. 掷一个骰子,观察朝上的面的点数,设事件“点数为奇数”,事件“点数为的整数倍”,若 , 分别表示事件 , 发生的概率,则( )A、 , B、 , C、 D、6. 已知 , 且 , 则向量在向量上的投影向量为( )A、 B、 C、 D、7. 如图,一个底面半径为2dm,母线长为的圆锥形封闭透明容器内部装有一种液体,当圆锥底面向下平放在水平桌面上时,液面的高度恰好为圆锥的高的 , 则当圆锥的顶点在桌面上,且底面平行于水平桌面时,液面的高度为( )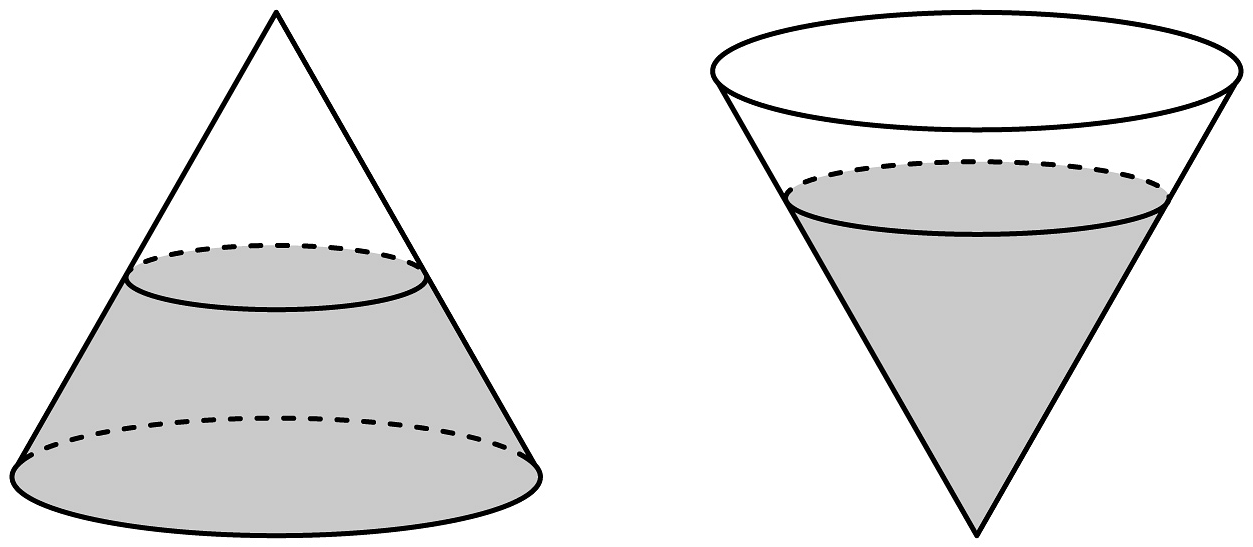 A、 B、2dm C、3dm D、8. 中国文化中的太极八卦图蕴含了现代哲学中的矛盾对立统一规律,如图1是八卦模型图,其平面图形记为图2中的正八边形 , 其中 , 若点P是其内部任意一点,则的取值范围是( )
A、 B、2dm C、3dm D、8. 中国文化中的太极八卦图蕴含了现代哲学中的矛盾对立统一规律,如图1是八卦模型图,其平面图形记为图2中的正八边形 , 其中 , 若点P是其内部任意一点,则的取值范围是( )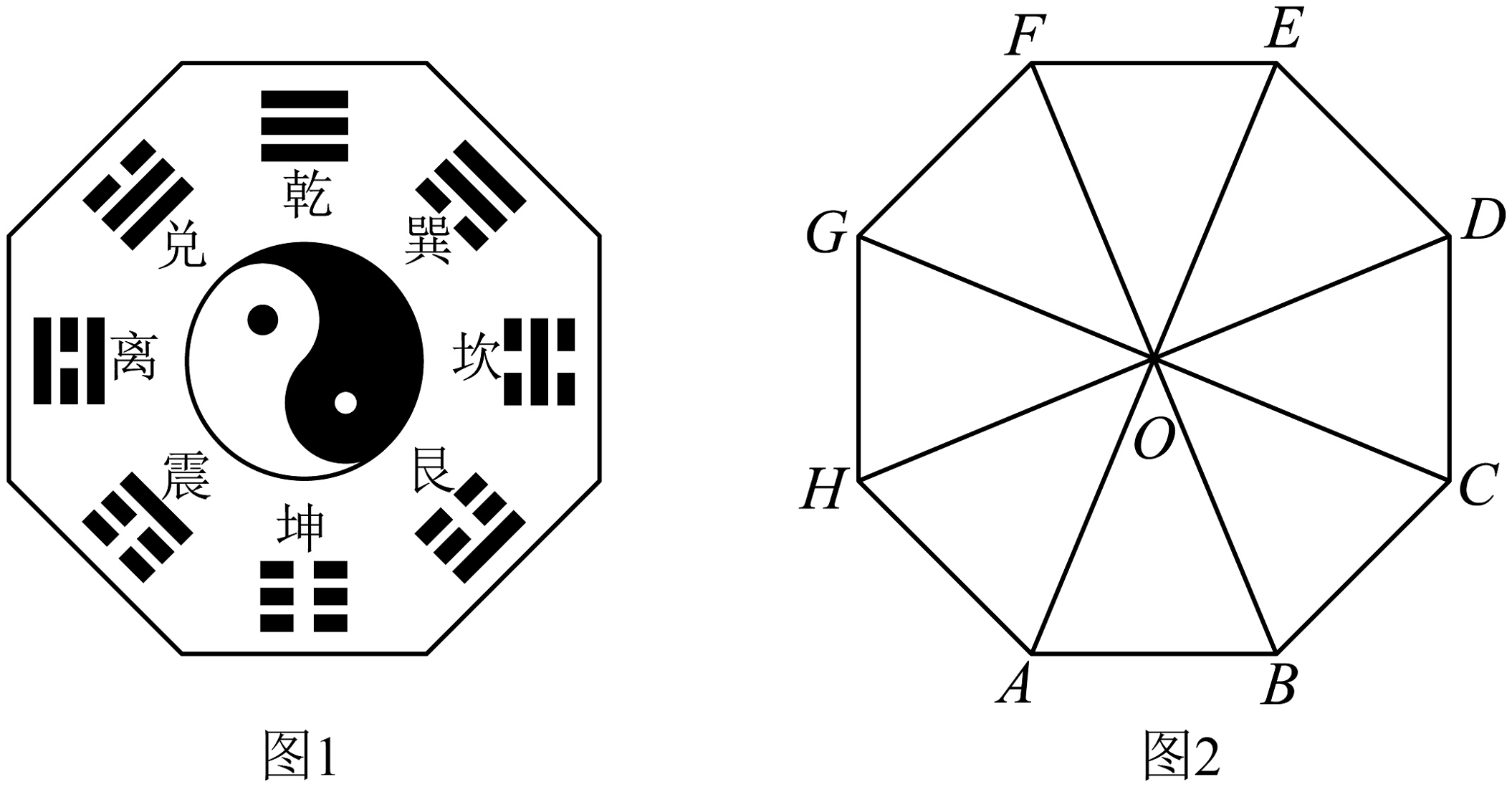 A、 B、 C、 D、
A、 B、 C、 D、二、多项选择题:本题共4小题,每小题6分,共24分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
-
9. 设是一个随机试验的两个事件,则( )A、若对立,则一定互斥 B、若 , 则 C、若 , 则相互独立 D、若 , 则一定对立10. 在中, , , 分别是内角 , , 的对边,下列说法正确的是( )A、若为锐角,则 B、若为锐角,则 C、若 , 则 D、若为锐角三角形,则11. 下列命题中正确的是( )A、若 , 则 B、若 , 则 C、已知 , , 是关于的方程的一个根,则 D、若复数满足 , 则的最大值为12. 如图,在棱长为2的正方体中,O为正方体的中心,M为的中点,F为侧面正方形内一动点,且满足平面 , 则( )
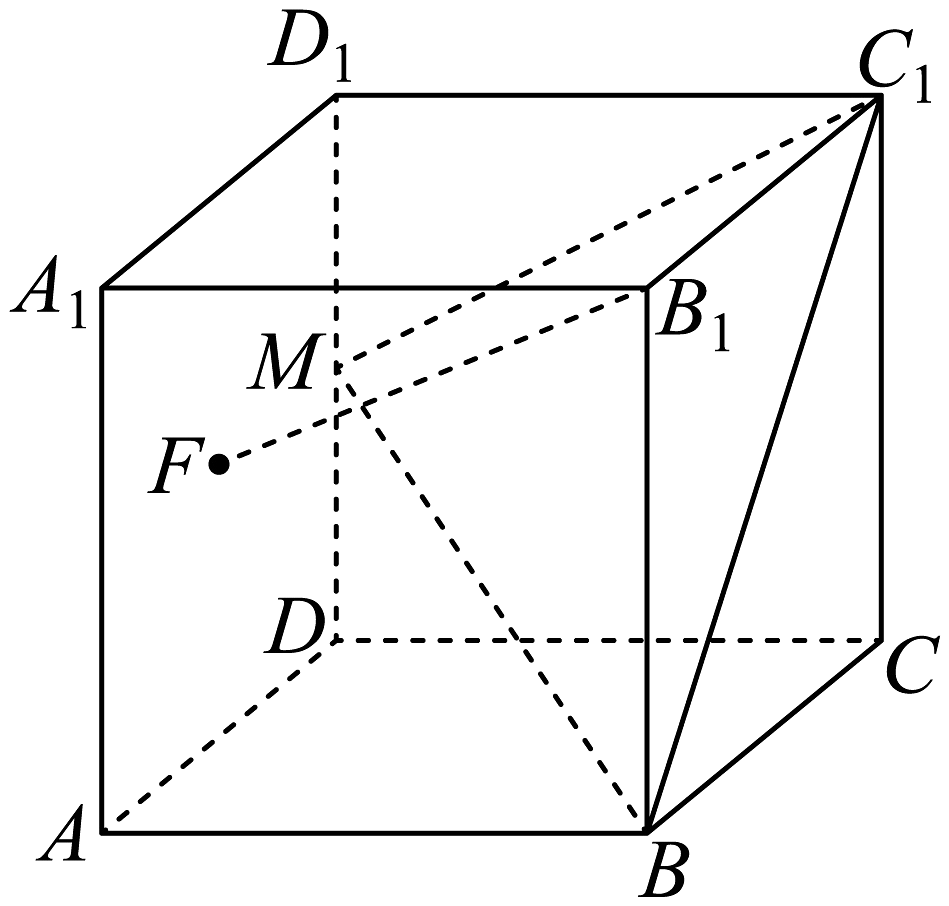 A、三棱锥的外接球表面积为 B、动点F的轨迹的线段为 C、三棱锥的体积为 D、若过A、M、三点作正方体的截面Ω,Q为Ω上一点,则线段长度最大值为
A、三棱锥的外接球表面积为 B、动点F的轨迹的线段为 C、三棱锥的体积为 D、若过A、M、三点作正方体的截面Ω,Q为Ω上一点,则线段长度最大值为三、填空题:本题共3小题,每小题5分,共15分.
-
13. 已知 , , 若 , 则 .14. 已知 , (i为虚数单位),则 .15. 如图,在梯形中, , , 将沿直线翻折至的位置,当三棱锥的体积最大时,则三棱锥的外接球的半径为 .
四、解答题:本题共5小题,共71分.解答应写出文字说明、证明过程或演算步骤.
-
16. 复数z满足为纯虚数,复数z在复平面内所对应的点在第一象限.(1)、已知 , 求复数z;(2)、已知 , 复数所对应的向量为 , 已知 , 求λ的值.17. 某学校为了解本校历史、物理方向学生的学业水平模拟测试数学成绩情况,分别从物理方向的学生中随机抽取60人的成绩得到样本甲,从历史方向的学生中随机抽取n人的成绩得到样本乙,根据两个样本数据分别得到如下直方图:
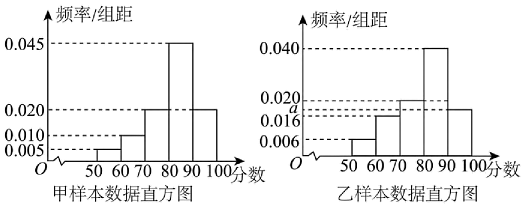
已知乙样本中数据在的有10个.
(1)、求n和乙样本直方图中a的值;(2)、试估计该校物理方向的学生本次模拟测试数学成绩的平均值和历史方向的学生本次模拟测试数学成绩的第75百位数(同一组中的数据用该组区间中点值为代表);(3)、采用分层抽样的方法从甲样本数据中分数在和的学生中抽取6人,并从这6人中任取2人,求这两人分数都在中的概率.18. 如图,四棱锥中,PC垂直平面ABCD, , ∥ , , , E是线段PB上的动点.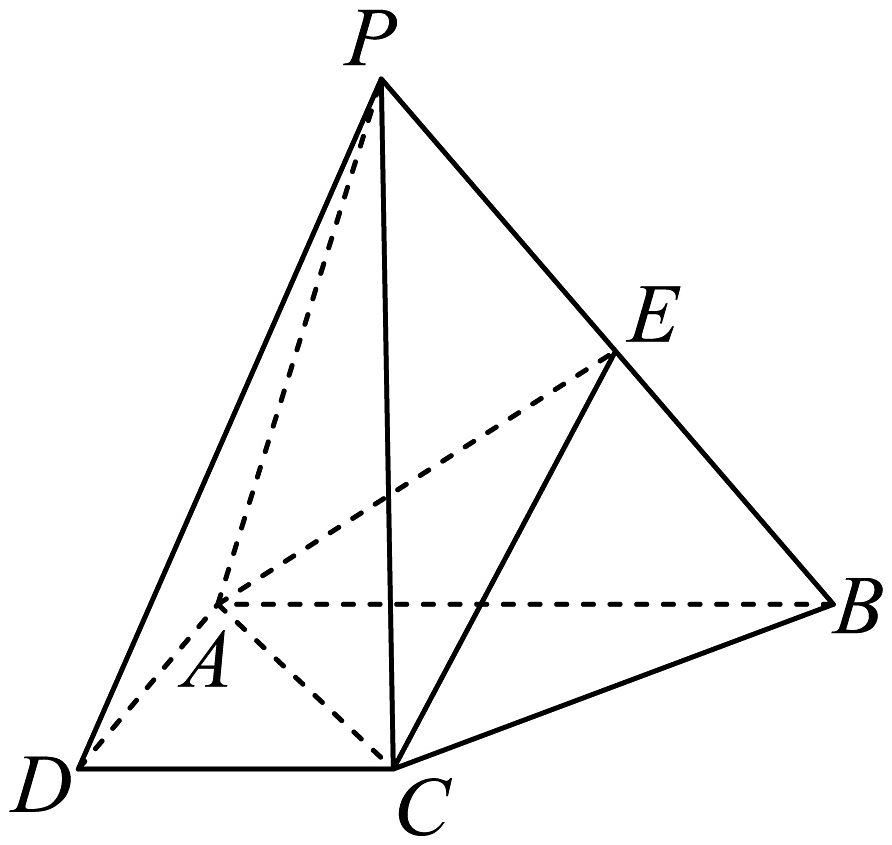 (1)、证明:;(2)、求二面角的正弦值;(3)、若∥平面 , 求点E的位置.19. 在中,角A,B,C所对的边分别为a,b,c,.(1)、求B;(2)、若点D为边BC的中点,点E,F分别在边AB,AC(包括顶点)上, , .设 , 将的面积S表示为的函数,并求S的取值范围.20. 对于两个平面向量 , , 如果有 , 则称向量是向量的“迷你向量”.(1)、若 , , 是的“迷你向量”,求实数x的取值范围;(2)、一只蚂蚁从坐标原点沿最短路径爬行到点处(且).蚂蚁每次只能沿平行或垂直于坐标轴的方向爬行一个单位长度,爬完第i次后停留的位置记为 , 设 . 记事件“蚂蚁经过的路径中至少有n个使得是的迷你向量”.(假设蚂蚁选择每条路径都是等可能的)
(1)、证明:;(2)、求二面角的正弦值;(3)、若∥平面 , 求点E的位置.19. 在中,角A,B,C所对的边分别为a,b,c,.(1)、求B;(2)、若点D为边BC的中点,点E,F分别在边AB,AC(包括顶点)上, , .设 , 将的面积S表示为的函数,并求S的取值范围.20. 对于两个平面向量 , , 如果有 , 则称向量是向量的“迷你向量”.(1)、若 , , 是的“迷你向量”,求实数x的取值范围;(2)、一只蚂蚁从坐标原点沿最短路径爬行到点处(且).蚂蚁每次只能沿平行或垂直于坐标轴的方向爬行一个单位长度,爬完第i次后停留的位置记为 , 设 . 记事件“蚂蚁经过的路径中至少有n个使得是的迷你向量”.(假设蚂蚁选择每条路径都是等可能的)①写出从坐标原点沿最短路径爬行到点的所有路线(如:右右右上)一般地,总数n步中恰有m步向上走其余各步向右走的方法总数为:
②当时,求;
③证明: .