湖南省永州市宁远县明德湘南中学2024-2025学年高二下学期期末考试数学试卷

试卷更新日期：2025-07-23 类型：期末考试

进入出卷网下载

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 已知集合 $M = \{x| y = ln (1 - 2 x)\}, N = \{y| y = e^{x}\}$ ，则 $M \cap N =$ （）

A、 $(\frac{1}{2}, + \infty)$ B、 $(- \infty, \frac{1}{2})$ C、 $(0, \frac{1}{2})$ D、 $\emptyset$

查看试题解析
2. 已知双曲线的标准方程为 $\frac{x^{2}}{k - 4} + \frac{y^{2}}{k - 5} = 1$ ，则该双曲线的焦距是（）

A、1 B、3 C、2 D、4

查看试题解析
3. 设等差数列 ${a_{n}}$ 的前n项和 $S_{n}$ ，若 $S_{3} = 9$ ， $S_{6} = 36$ ，则 $a_{7} + a_{8} + a_{9} =$ （）

A、18 B、27 C、45 D、63

查看试题解析
4. 若古典概型的样本空间 $Ω = \{1, 2, 3, 4\}$ ，事件 $A = \{1, 2\}$ ，甲：事件 $B = Ω$ ，乙：事件 $A, B$ 相互独立，则甲是乙的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
5. 冬季是流感高发期，其中甲型流感病毒传染性非常强．基本再生数 $R_{0}$ 与世代间隔 $T$ 是流行病学基本参考数据．某市疾控中心数据库统计分析，可以用函数模型 $W (t) = 2^{r t}$ 来描述累计感染甲型流感病毒的人数 $W (t)$ 随时间t， $t \in Z$ （单位：天）的变化规律，其中指数增长率 $r$ 与基本再生数 $R_{0}$ 和世代间隔T之间的关系近似满足 $R_{0} = 1 + r T$ ，根据已有数据估计出 $R_{0} = 4$ 时， $T = 12$ ．据此回答，累计感染甲型流感病毒的人数增加至 $W (0)$ 的3倍至少需要（参考数据： $\lg 2 \approx 0.301$ ， $\lg 3 \approx 0.477$ ）（）

A、6天 B、7天 C、8天 D、9天

查看试题解析
6. 如图是两个底面半径都为1的圆锥底面重合在一起构成的几何体，上面圆锥的侧面积是下面圆锥侧面积的2倍， $A P ⊥ A Q$ ，则 $P Q =$ （）

A、 $\frac{7}{4}$ B、 $\frac{\sqrt{26}}{2}$ C、 $\frac{5}{2}$ D、3

查看试题解析
7. 已知 $(\frac{1}{\tan \frac{α - β}{2}} - \tan \frac{α - β}{2}) [1 + \tan (α - β) \tan \frac{α - β}{2}] = 6$ ， $\tan α \tan (\frac{π}{2} - β) = 3$ ，则 $\cos (4 α + 4 β) =$ （）

A、 $- \frac{79}{81}$ B、 $\frac{79}{81}$ C、 $- \frac{49}{81}$ D、 $\frac{49}{81}$

查看试题解析
8. 已知球 $O$ 的直径为 $P C = 2 \sqrt{3}, A 、 B$ 是球面上两点，且 $P A = P B = \sqrt{3}, ∠ A P B = \frac{π}{3}$ ，则三棱锥 $P - A B C$ 的体积（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{6}}{2}$ D、 $\sqrt{6}$

查看试题解析

二、多项选择题：本大题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求，全部选对得6分，部分选对得部分分，选错得0分.

9. 某学校高一年级学生有900人，其中男生500人，女生400人，为了获得该校高一全体学生的身高信息，现采用样本量比例分配的分层随机抽样方法抽取了容量为180的样本，经计算得男生样本的均值为170，方差为19，女生样本的均值为161，方差为28，则下列说法中正确的是（）

A、男生样本容量为100 B、抽取的样本的方差为43 C、抽取的样本的均值为166 D、抽取的样本的均值为165.5

查看试题解析
10. 已知 $x \geq 1$ ， $y > 1$ ，且 $x y = 4$ ，则（）

A、 $1 \leq x \leq 4$ ， $1 < y < 4$ B、 $4 \leq x + y \leq 5$ C、 $\frac{y}{x}$ 最大值为4 D、 $4 x + y^{2}$ 的最小值为12

查看试题解析
11. 已知数列 $\{a_{n}\}$ 的前n项和为 $S_{n}$ ，且 $2 S_{n} S_{n + 1} + S_{n + 1} = 3$ ， $a_{1} = α (0 < α < 1)$ ，则（）

A、当 $0 < α < \frac{\sqrt{13} - 1}{4}$ 时， $a_{2} > a_{1}$ B、 $a_{3} > a_{2}$ C、数列 $\{S_{2 n - 1}\}$ 单调递增， $\{S_{2 n}\}$ 单调递减 D、当 $α = \frac{3}{4}$ 时，恒有 $\sum_{k = 1}^{n} |S_{k} - 1| < \frac{5}{4}$

查看试题解析

三、填空题：本题共3小题，每小题5分，共15分.

12. 在 ${(1 + a x)}^{n}$ （其中 $n \in N^{*}, a \neq 0$ ）的展开式中， $x$ 的系数为 $- 10$ ，各项系数之和为 $- 1$ ，则 $n =$ .

查看试题解析
13. 已知四面体 $A - B C D$ ，其中 $A D = B C = 2$ ， $C D = A B = \sqrt{5}$ ， $A C = B D = \sqrt{7}$ ， $E$ 为 $C D$ 的中点，则直线 $A D$ 与 $B E$ 所成角的余弦值为；四面体 $A - B C D$ 外接球的表面积为．

查看试题解析
14. 函数 $f (x) = 2 s i n (ω x + \frac{π}{6})$ （ $ω > 0$ ）在区间 $(\frac{π}{6} ， \frac{π}{2})$ 上有且只有两个零点，则 $ω$ 的取值范围是.

查看试题解析

四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.

15. 在锐角 $△ A B C$ 中，内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，已知 $2 a \sin C - \sqrt{3} c = 0$ ．

(1)、求 $A$ ；

(2)、求 $4 \sin B - 4 \sin C$ 的取值范围．

查看试题解析
16. 如图，P为圆锥的顶点， $A C$ 为圆锥底面的直径， $△ P A C$ 为等边三角形，O是圆锥底面的圆心． $△ A B D$ 为底面圆O的内接正三角形，且边长为 $2 \sqrt{3}$ ，点E为线段 $P C$ 中点．

(1)、求证：平面 $B E D ⊥$ 平面 $A B D$ ；

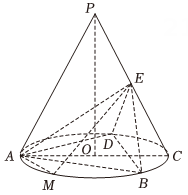(2)、M为底面圆O的劣弧 $A B$ 上一点，且 $∠ A C M = 30 °$ ．求平面 $A M E$ 与平面 $P A C$ 夹角的余弦值．

查看试题解析
17. 有 $n^{2} (n \geq 4)$ 个正数，排成n行n列的数表：其中 $a_{i j}$ 表示位于第i行，第j列的数，数表中每一行的数成等差数列，每一列的数成等比数列，并且所有公比相等，已知 $a_{24} = 1$ ， $a_{42} = \frac{1}{8}$ ， $a_{43} = \frac{3}{16}$ .
$(\begin{matrix} a_{11} & a_{12} & a_{13} & a_{14} & \dots & a_{1 n} \\ a_{21} & a_{22} & a_{23} & a_{24} & \dots & a_{2 n} \\ a_{31} & a_{32} & a_{33} & a_{34} & \dots & a_{3 n} \\ a_{41} & a_{42} & a_{43} & a_{44} & \dots & a_{4 n} \\ \dots & \dots & \dots & \dots & \dots & \dots \\ a_{n 1} & a_{n 2} & a_{n 3} & a_{n 4} & \dots & a_{n n} \end{matrix})$

(1)、求公比.

(2)、求 $a_{11} + a_{22} + \dots + a_{n n}$ .

查看试题解析
18. 已知函数 $f (x) = \frac{x^{2}}{e^{a x}}$ ，其中 $a > 0$ ．

(1)、若 $f (x)$ 在 $(0, 2]$ 上单调递增，求 $a$ 的取值范围；

(2)、当 $a = 1$ 时，若 $x_{1} + x_{2} = 4$ 且 $0 < x_{1} < 2$ ，比较 $f (x_{1})$ 与 $f (x_{2})$ 的大小，并说明理由

查看试题解析
19. 马尔科夫链因俄国数学家安德烈・马尔科夫得名，其过程具备“无记忆”的性质，即第 $n + 1$ 次状态的概率分布只跟第 $n$ 次的状态有关，与第 $n - 1, n - 2, n - 3, \dots$ 次状态无关.马尔科夫链是概率统计中的一个重要模型，也是机器学习和人工智能的基石，在强化学习、自然语言处理、金融领域、天气预测等方面都有着极其广泛的应用.现有 $A, B$ 两个盒子，各装有2个黑球和1个红球，现从 $A, B$ 两个盒子中各任取一个球交换放入另一个盒子，重复进行 $n (n \in N^{*})$ 次这样的操作后，记 $A$ 盒子中红球的个数为 $X_{n}$ ，恰有1个红球的概率为 $p_{n}$ .

(1)、求 $p_{1}, p_{2}$ 的值；

(2)、求 $p_{n}$ 的值（用 $n$ 表示）；

(3)、求证： $X_{n}$ 的数学期望 $E (X_{n})$ 为定值.

查看试题解析