浙江省舟山市2024-2025学年高二下学期6月期末检测数学试题
试卷更新日期:2025-06-29 类型:期末考试
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 设集合 , , 则( )A、 B、 C、 D、2. 已知复数(为虚数单位),则的虚部为( )A、 B、 C、 D、3. 已知 , 则( )A、 B、 C、 D、4. 展开式中常数项为( )A、48 B、 C、24 D、5. 若 , 函数为上的奇函数,则是的( )A、充分不必要条件 B、必要不充分条件 C、既不充分也不必要条件 D、充要条件6. 甲、乙、丙、丁、戊五位同学课间玩“击鼓传花”游戏.第1次由甲传给乙、丙、丁、戊四人中的任意一人,第2次由持花者传给另外四人中的任意一人,往后依此类推,经过4次传花,花仍回到甲手中,则传法总数为( )A、36 B、48 C、52 D、647. 已知函数在上单调递减,则的取值范围是( )A、 B、 C、 D、8. 记函数.已知函数 , , , 若有且只有个零点,则的取值范围是( )A、 B、 C、 D、
二、多项选择题(本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
-
9. 下列说法正确的是( )A、经验回归方程为时,变量与变量成正相关 B、在做回归分析时,残差图中残差点分布的带状区域的宽度越窄表示回归效果越好 C、若随机变量 , 且 , 则 D、已知随机事件、 , 若 , , 则10. 定义在上的函数满足 , 则( )A、函数的解析式为 B、函数图象的对称轴为直线 C、函数的单调递增区间为 D、函数在上的最大值为11. 已知正方体的棱长为3,以下说法正确的是( )A、若点为正方形内部及边界上的动点,且满足 , 则动点的轨迹长度是 B、若点为正方形内部及边界上任意一点,则存在点使得点 , 到平面的距离之和等于 C、若点在正方体的内切球表面上运动,且面 , 则的最小值为 D、若点满足 , 则动点构成的平面截三棱锥所得截面的面积为
三、填空题(本大题共3小题,每小题5分,共15分)
-
12. 有一组数据:、、、、.则其第百分位数为.13. 命题“ , 为假命题”,则实数的取值范围为.14. 已知实数、满足 , 则的最小值为.
四、解答题(本大题共5小题,共77分,解答应写出文字说明、证明过程或演算步骤)
-
15. 在中,、、分别为的内角、、的对边,满足 , 为的中点.(1)、求角的大小;(2)、若 , , 求线段的长度.16. 已知平面向量、满足 , , .(1)、求在上的投影向量(结果用表示);(2)、求;(3)、若 , 求.17. 如图,已知四棱台 , 点在底面上的射影落在线段上(不含端点),底面为直角梯形, , , , .
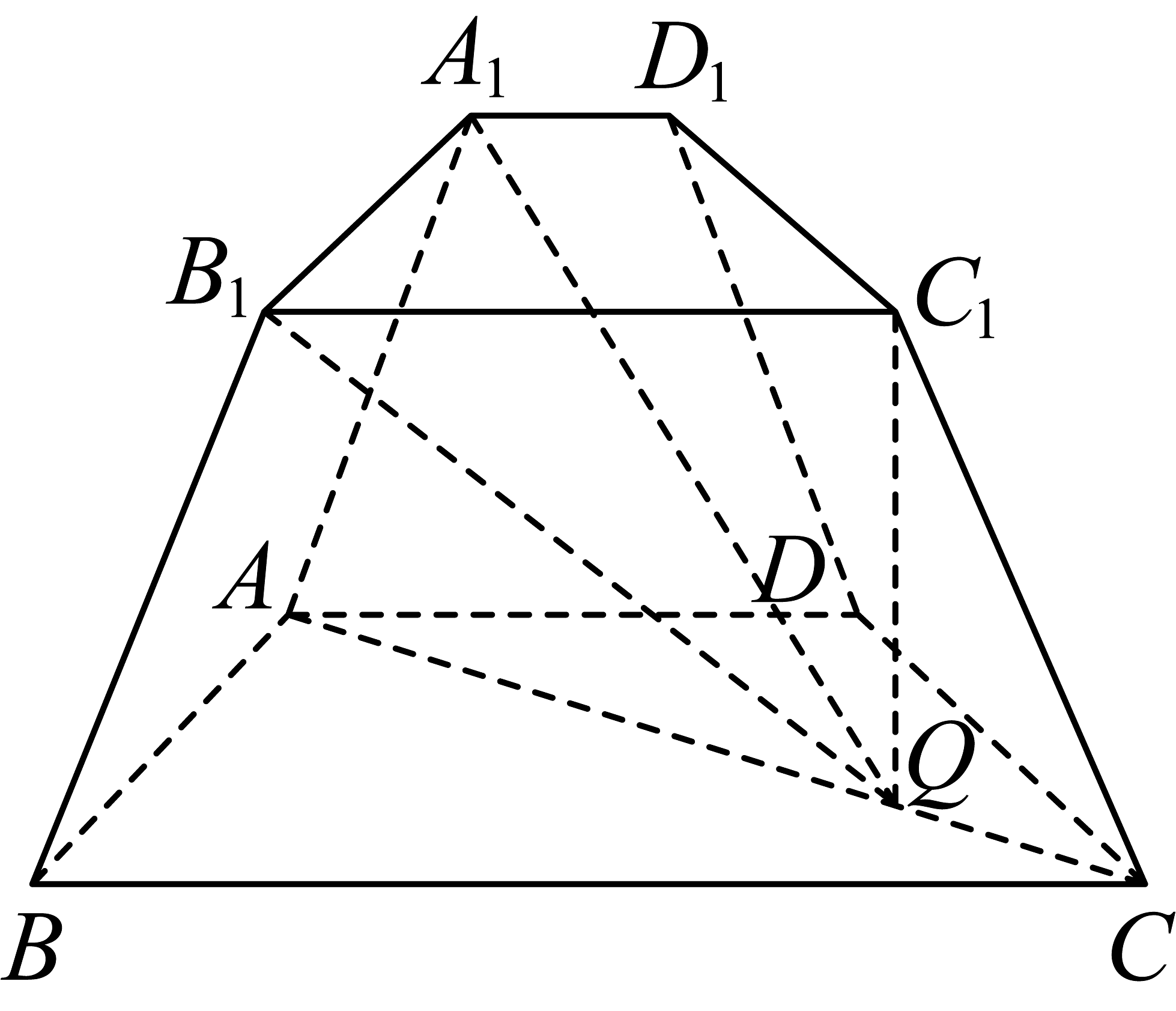 (1)、求证:平面;(2)、若二面角的大小为;
(1)、求证:平面;(2)、若二面角的大小为;(ⅰ)求直线与平面所成的角;
(ⅱ)若四边形为等腰梯形, , 求平面与平面夹角的正切值.
18. 2025年,某卫视推出了“最强大脑围棋版争霸赛”,堪称围棋界史上最激烈的国际赛事,以“棋艺封神,一站扬名”为口号,致力于推广围棋文化和智力竞技.受此启发,某中学为了让学生亲身体验围棋比赛的精彩和激烈,激发学生的思维活力,特别举办了“校园棋王争霸赛”.根据已报名的学生资料统计,有的学生学过围棋,将频率视为概率.(1)、从已报名选手中任取3名学生,记其中学过围棋的学生数为 , 求的分布列与数学期望;(2)、经过海选,最终决定、、、、、、、八位棋手参加棋王争霸赛,比赛分预赛、半决赛和决赛三个阶段,采用淘汰制决出冠军.预赛共有四场,八位棋手赛前抽签确定比赛位置,获胜的四人进入半决赛,依次类推,在决赛中,胜者为冠军,负者为亚军。已知~这7位棋手互相对弈时,获胜概率均为 , 棋手与其他棋手对弈时,获胜的概率为 , 每局对弈结果相互独立,无和棋情况.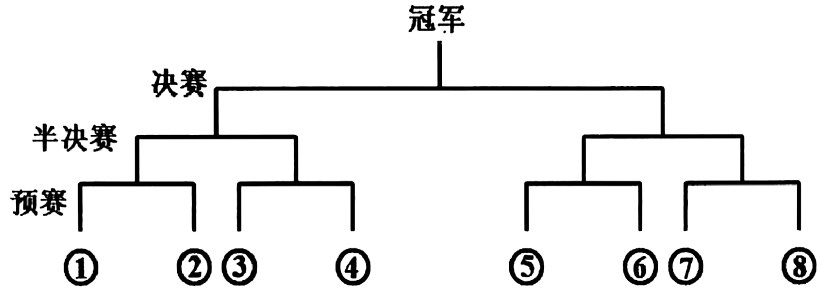
(ⅰ)求棋手最终夺冠的概率;
(ⅱ)求棋手与有过对弈且最终获得亚军的概率.
19. 函数的定义域为;①若对 , 都有成立,则称在上为凹函数(当且仅当时,等号成立),且凹函数有以下性质:对都有(当且仅当时,等号成立).
②若对 , 都有成立,则称在上为凸函数(当且仅当时,等号成立),且凸函数有以下性质:对都有(当且仅当时,等号成立).
(1)、判断函数在上是否具有凹凸性,并用上述定义法证明你的结论.(2)、设为的周长,为的面积;(i)求:的取值范围;
(ii)证明:.