广东省清远市2024-2025学年高二下学期6月期末数学试题

试卷更新日期：2025-06-27 类型：期末考试

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. $A_{5}^{3} + A_{3}^{2} =$ （）

A、8 B、13 C、63 D、66

查看试题解析
2. 已知 $f (x) = \frac{2}{x} + 1$ ，则 $\lim_{Δ x \to 0} \frac{f (1 + Δ x) - f (1)}{Δ x}$ 的值为（）

A、-1 B、-2 C、0 D、2

查看试题解析
3. 某活动室有足球和篮球，从中随机挑选2个球，若这2个球中足球个数为 $X$ ，且 $X$ 的分布列如下表所示，则 $p =$ （）
$X$
0
1
2
$P (X)$
$7 p$
$\frac{7}{15}$
$p$

A、 $\frac{1}{15}$ B、 $\frac{1}{5}$ C、 $\frac{4}{15}$ D、 $\frac{7}{15}$

查看试题解析
4. 某班级有 $42$ 名学生，其中男生､女生的人数及是否喜爱篮球的人数如表所示，从这 $42$ 名学生中随机选择 $1$ 人作为体育课代表，若选到的学生喜爱“篮球”，则该学生是女生的概率为（）
喜爱“篮球”
不喜爱“篮球”
合计
男生
$15$
$7$
$22$
女生
$10$
$10$
$20$
合计
$25$
$17$
$42$

A、 $\frac{3}{5}$ B、 $\frac{2}{5}$ C、 $\frac{1}{2}$ D、 $\frac{5}{21}$

查看试题解析
5. 如图，要让电路从 $A$ 处到 $B$ 处只有一条支路接通，则不同的路径有（）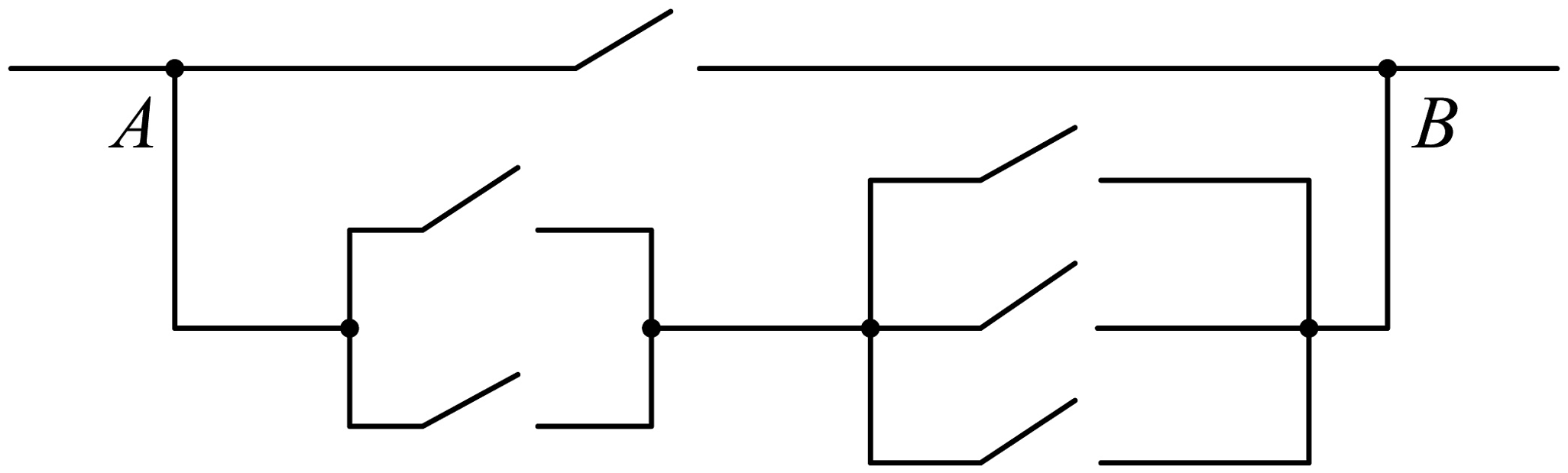

A、5种 B、6种 C、7种 D、9种

查看试题解析
6. 已知 $X \sim B (5, 0.6)$ ，若 $Y = 2 X + 1$ ，则 $E (Y) + D (Y) =$ （）

A、-1 B、-2 C、11.8 D、2

查看试题解析
7. 已知函数 $f (x) = a x^{2} - 2$ 的图象在点 $(\sqrt{3}, f (\sqrt{3}))$ 处的切线的倾斜角为 $\frac{π}{3}$ ，则曲线 $y = f (x)$ 在点 $(1, f (1))$ 处的切线的方程为（）

A、 $2 x + 2 y - 5 = 0$ B、 $2 x - 2 y - 5 = 0$ C、 $2 x - 2 y + 1 = 0$ D、 $2 x + 2 y + 1 = 0$

查看试题解析
8. 已知数列： $1, 2, 3, \dots, 2025$ ，从中任选三项组成一个新数列，则所有新数列中的最小项之和为（）

A、 $3 C_{2025}^{4}$ B、 $3 C_{2026}^{4}$ C、 $6 C_{2025}^{4}$ D、 $6 C_{2026}^{4}$

查看试题解析

二、多选题：本题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.

9. 已知 ${(1 - 2 x)}^{6} = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4} + a_{5} x^{5} + a_{6} x^{6}$ ，则下列说法正确的是（）

A、 $a_{0} = 1$ B、 $a_{2} = 240$ C、 $a_{1} + a_{2} + a_{3} + a_{4} + a_{5} + a_{6} = 0$ D、 $a_{1} + a_{3} + a_{5} = - 364$

查看试题解析
10. 在 $A, B, C$ 三个地区暴发了流感，这三个地区分别有 $6 %, 5 %, 4 %$ 的人患了流感，假设这三个地区的人口数之比为 $5 : 7 : 8$ ，现从这三个地区中任意选取一个人，下列结论正确的是（）

A、若此人选自 $B$ 地区，则其患流感的概率为0.05 B、此人患流感的概率为0.0485 C、若此人患流感，则其选自 $A$ 地区的概率为 $\frac{30}{97}$ D、若此人患流感，则其选自 $C$ 地区的概率为 $\frac{34}{97}$

查看试题解析
11. 已知函数 $f (x) = x - ln x + a (a \in R)$ ，则下列说法正确的是（）

A、若 $f (x)$ 有两个零点，则 $a \leq - e$ B、若 $g (x) = f (x) - f (2 - x)$ ，则 $g (x)$ 无最值 C、当 $a = 1$ 时，方程 $f (x) = 3 ln x + \frac{3}{x}$ 有唯一实根 D、若存在 $x_{0} \in (0, + \infty)$ ，使得 $f (x_{0}) \leq (1 - a) x_{0} + 2$ ，则 $a \leq 1$

查看试题解析

三、填空题：本题共3小题，每小题5分，共15分.

12. 某班女生的身高 $X$ （单位：cm）近似服从正态分布 $N (163, 4)$ ，从中随机选取一人，则 $P (163 \leq X \leq 165) \approx$ .（精确到0.0001，参考数据：若 $X \sim N (μ, σ^{2})$ ，则 $P (μ - σ \leq X \leq μ + σ) \approx 0.6827, P (μ - 2 σ \leq X \leq μ + 2 σ) \approx 0.9545$ ， $P (μ - 3 σ \leq X \leq μ + 3 σ) \approx 0.9973$ ）

查看试题解析
13. 某校安排4位老师在期末考试的3天值班，要求每人需要值班1天或2天，且每天有两人值班，则不同的值班方案有种.

查看试题解析
14. 小李家共有10只信鸽，其中戴盔鸽有3只，李种鸽有 $n (2 \leq n \leq 5$ 且 $n \neq 4)$ 只，其余的为蓝鸽，且随机取出2只信鸽，其品种不相同的概率是 $\frac{11}{15}$ .现随机取出2只信鸽，若取出1只蓝鸽记10分，取出1只戴盔鸽记20分，取出1只李种鸽记30分.用 $X$ 表示取出的2只信鸽的分数之和，则 $X$ 的数学期望为.

查看试题解析

四、解答题：本题共5小题，共77分.解答应写出必要的文字说明､证明过程及演算步骤.

15. 在研究某类杨树的树高与胸径（树的主干在地面以上 $1.3 m$ 处的直径）之间的关系时，某研究员收集的一些数据如表1所示.

(1)、由表1数据，求胸径 $d$ 与树高 $h$ 的平均值；（胸径 $d$ 精确到 $0.1 cm$ ，树高 $h$ 精确到 $0.1 m$ ）

(2)、根据这些数据，可建立该类杨树树高 $\hat{h}$ （单位： $m$ ）关于胸径 $d$ （单位： $cm$ ）的一元线性回归模型为 $\hat{h} = 0.25 d + \hat{a}$ ，用（1）中结果求 $\hat{a}$ 的值并估计胸径为 $30 cm$ 的该类杨树的树高；（精确到 $0.1 m$ ）

(3)、若这12棵杨树树龄相同，分别种植于南坡和北坡，且成材情况如表2所示，根据 $α = 0.1$ 的独立性检验，能否认为树龄相同的这类杨树是否成材与种植位置有关联？
编号
1
2
3
4
5
6
胸径 $/ cm$
18.1
20.1
22.2
24.4
26.0
28.3
树高 $/ m$
18.8
19.2
21.0
21.0
22.1
22.1
编号
7
8
9
10
11
12
胸径 $/ cm$
29.6
32.4
33.7
35.7
38.3
40.2
树高 $/ m$
22.4
22.6
23.0
24.3
23.9
24.7
表1
种植位置
成材情况
合计
成材
未成材
南坡
5
1
6
北坡
2
4
6
合计
7
5
12
表2
参考公式及数据： $χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ .
$α$
0.1
0.05
0.01
0.001
$x_{α}$
2.706
3.841
6.635
10.828

查看试题解析
16. 如图，在三棱锥 $A - B C D$ 中，底面 $△ B C D$ 是等腰直角三角形， $A D ⊥$ 底面 $B C D, A D = B C = C D = 2, M$ 是 $A D$ 的中点， $P$ 是 $B M$ 的中点，且 $\vec{A Q} + 3 \vec{C Q} = \vec{0}$ .

(1)、证明： $P Q$ $∥$ 平面 $B C D$ ；

(2)、求直线 $B M$ 与平面 $A B C$ 所成角的正弦值.

查看试题解析
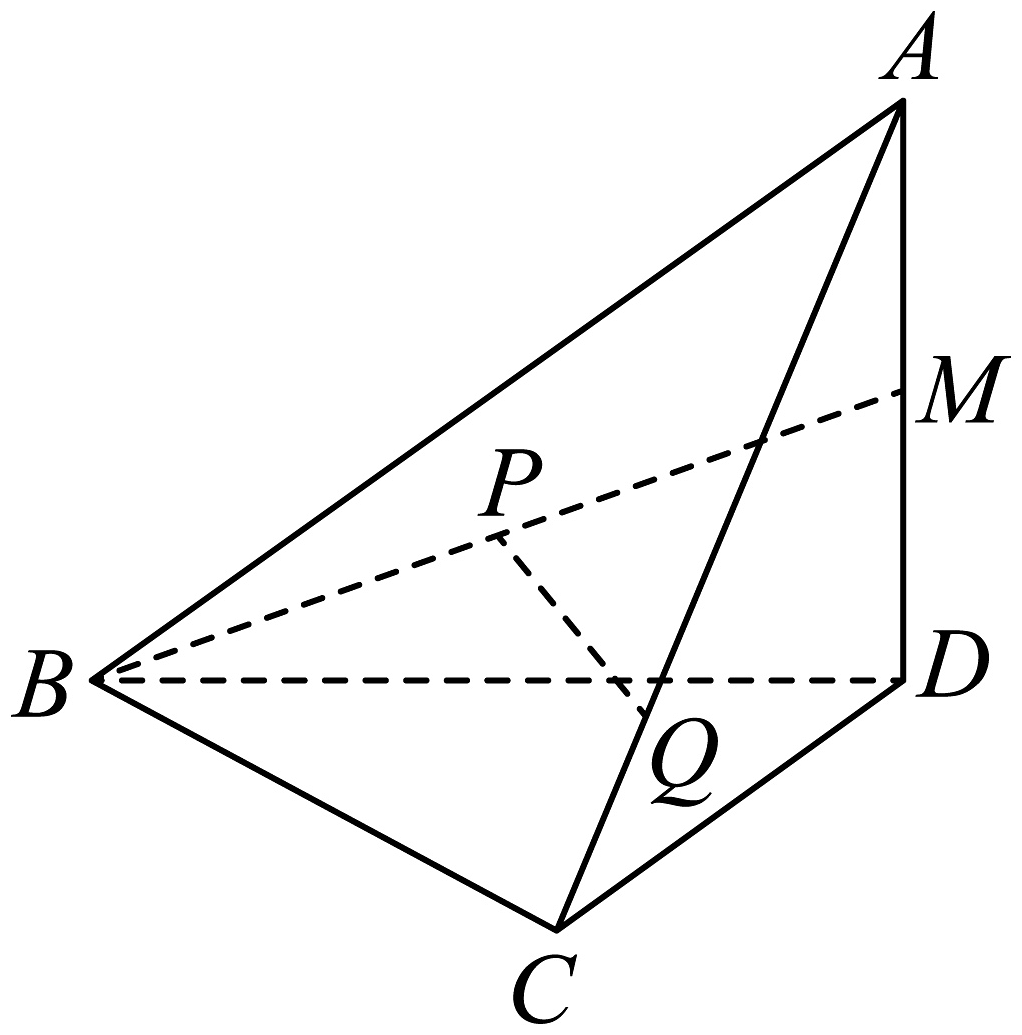17. 已知双曲线 $C_{1} : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 与椭圆 $C_{2} : \frac{x^{2}}{36} + \frac{y^{2}}{16} = 1$ 的焦点相同，且离心率之比为 $3 : 1$ .

(1)、求双曲线 $C_{1}$ 的方程；

(2)、若直线 $l : x - n y + 3 = 0$ 与双曲线 $C_{1}$ 的左､右两支分别交于 $P, Q$ 两点，记点 $P$ 关于 $x$ 轴的对称点为 $P^{'}$ ，证明：直线 $P^{'} Q$ 过定点，并求出该定点的坐标.

查看试题解析
18. 甲､乙两名操作员对 $A, B, C$ 三种电子信息传递元件进行随机连接检测，并制定如下标准：第一次由 $A$ 元件将信息传出，每次传递时，传递元件都等可能地将信息传递给另外两个元件中的任何一个，若第三次传递后，信息在 $A$ 元件中，则该组检测成功，否则该组检测失败.若该组检测成功，则由原操作员继续操作下一组检测；反之，则由另一操作员按上述规则继续操作下一组检测.

(1)、求一组随机连接检测成功的概率；

(2)、若第1次从甲开始进行随机连接检测，记在前4次检测中，乙操作的次数为 $X$ ，求随机变量 $X$ 的分布列与期望；

(3)、若第1次从乙开始进行连接检测，求第 $n$ 次由乙操作的概率 $P_{n}$ .

查看试题解析
19. 已知函数 $f (x) = a e^{x} - \frac{1}{3} x^{3} + 3 x (a \in R)$ 的导函数为 $f^{'} (x)$ .

(1)、当 $a = 0$ 时，求 $f (x)$ 的极值；

(2)、若 $a > 0, g (x) = \frac{x [f (x) + \frac{1}{3} x^{3} - 3 x] - e^{x}}{x - 1}$ 在 $(2, + \infty)$ 上不单调，求 $a$ 的取值范围；

(3)、已知 $h (x) = \frac{f^{'} (x) - 3}{x} + ln x$ ，若 $h (x)$ 在定义域内有三个不同的极值点 $x_{1}, x_{2}, x_{3}$ ，且满足 $h (x_{1}) \cdot h (x_{2}) \cdot h (x_{3}) \geq \frac{1}{e} - 1$ ，求实数 $a$ 的取值范围.

查看试题解析

	喜爱“篮球”	不喜爱“篮球”	合计
男生	$15$	$7$	$22$
女生	$10$	$10$	$20$
合计	$25$	$17$	$42$

编号	1	2	3	4	5	6
胸径 $/ cm$	18.1	20.1	22.2	24.4	26.0	28.3
树高 $/ m$	18.8	19.2	21.0	21.0	22.1	22.1
编号	7	8	9	10	11	12
胸径 $/ cm$	29.6	32.4	33.7	35.7	38.3	40.2
树高 $/ m$	22.4	22.6	23.0	24.3	23.9	24.7

种植位置	成材情况		合计
种植位置	成材	未成材	合计
南坡	5	1	6
北坡	2	4	6
合计	7	5	12

$X$	0	1	2
$P (X)$	$7 p$	$\frac{7}{15}$	$p$

$α$	0.1	0.05	0.01	0.001
$x_{α}$	2.706	3.841	6.635	10.828