湖南省长沙市雅礼教育集团2024-2025学年高一下学期6月期末考试数学试题
试卷更新日期:2025-07-10 类型:期末考试
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是正确的.
-
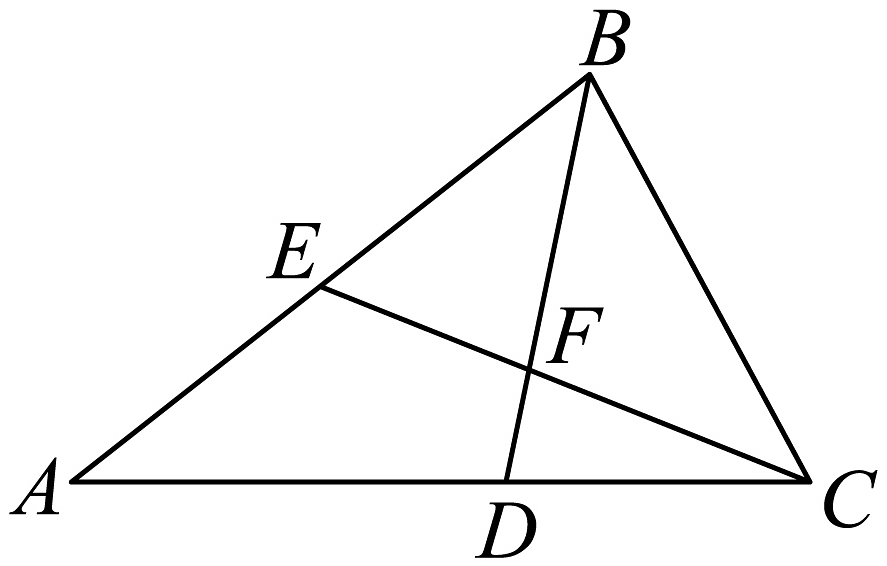
1. 经过两点的直线的倾斜角为 , 则的值为( )A、-2 B、1 C、3 D、42. 若复数是纯虚数,则A、3 B、5 C、 D、3. 如图,空间四边形中, , , , 点在线段上,且 , 点为中点,则等于( )
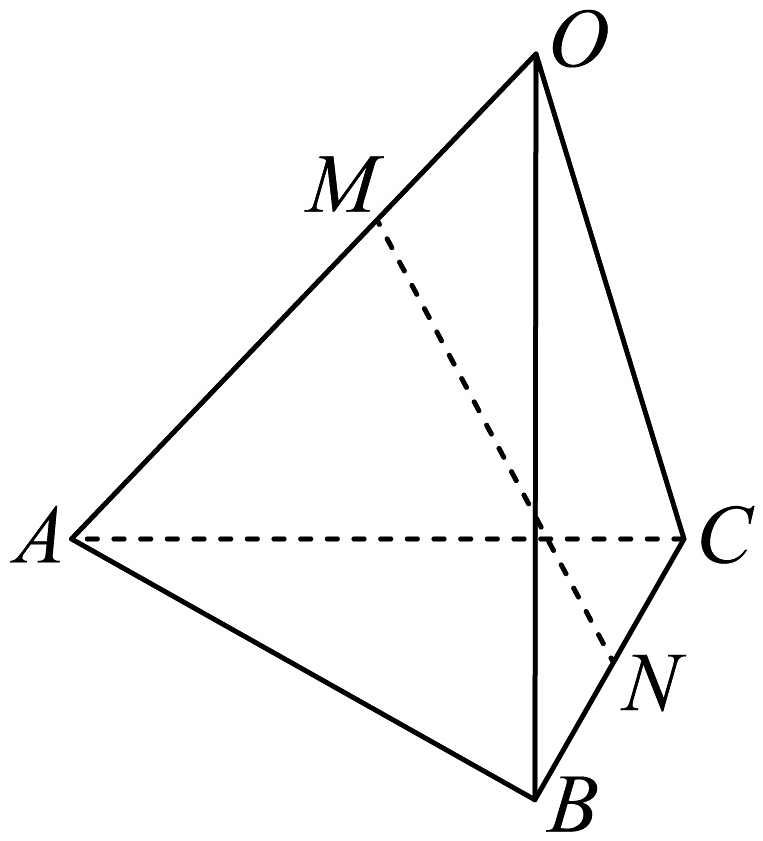 A、 B、 C、 D、4. 已知为不同的直线,为不同的平面,下列命题为假命题的是( )A、 B、 C、 D、5. 在中,角A,B,C的对边分别为a,b,c,若 , 则的面积( )A、1 B、 C、 D、6. 已知两个单位向量满足 , 则( )A、0 B、 C、1 D、27. 一艘海轮从处出发,以每小时50海里的速度沿南偏东的方向直线航行,2小时后到达处,在处有一座灯塔,海轮在处观察灯塔,其方向是南偏东 , 在处观察灯塔.其方向是北偏东 , 那么两点间的距离是( )A、海里 B、海里 C、海里 D、海里8. 抛一枚质地均匀的骰子两次,设事件表示“第二次朝上的数字为偶数”,则下列事件中与事件相互独立的是( )A、第二次朝上的数字是奇数 B、第二次朝上的数字为2 C、两次朝上的数字之和为9 D、两次朝上的数字之和为10
A、 B、 C、 D、4. 已知为不同的直线,为不同的平面,下列命题为假命题的是( )A、 B、 C、 D、5. 在中,角A,B,C的对边分别为a,b,c,若 , 则的面积( )A、1 B、 C、 D、6. 已知两个单位向量满足 , 则( )A、0 B、 C、1 D、27. 一艘海轮从处出发,以每小时50海里的速度沿南偏东的方向直线航行,2小时后到达处,在处有一座灯塔,海轮在处观察灯塔,其方向是南偏东 , 在处观察灯塔.其方向是北偏东 , 那么两点间的距离是( )A、海里 B、海里 C、海里 D、海里8. 抛一枚质地均匀的骰子两次,设事件表示“第二次朝上的数字为偶数”,则下列事件中与事件相互独立的是( )A、第二次朝上的数字是奇数 B、第二次朝上的数字为2 C、两次朝上的数字之和为9 D、两次朝上的数字之和为10二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对得6分,部分选对的得部分分,有选错的得0分.
-
9. 已知为虚数单位,以下四个说法中正确的是( )A、 B、若 , 则复平面内对应的点位于第二象限 C、复数 , D、若复数满足 , 则的最大值为610. 下列说法正确的有( )A、若事件与事件是互斥事件,则 B、若事件与事件是对立事件,则 C、把红、橙、黄3张纸牌随机分给甲、乙、丙3人,每人分得1张,则事件“甲分得的不是红牌”与事件“乙分得的不是红牌”是互斥事件 D、某人打靶时连续射击三次,则事件“至少有两次中靶”与事件“至多有一次中靶”是对立事件11. 如图,正方体的棱长为1,P为的中点,Q为线段上的动点,过点A,P,Q的平面截该正方体所得截面记为S,则下列命题正确的是( )
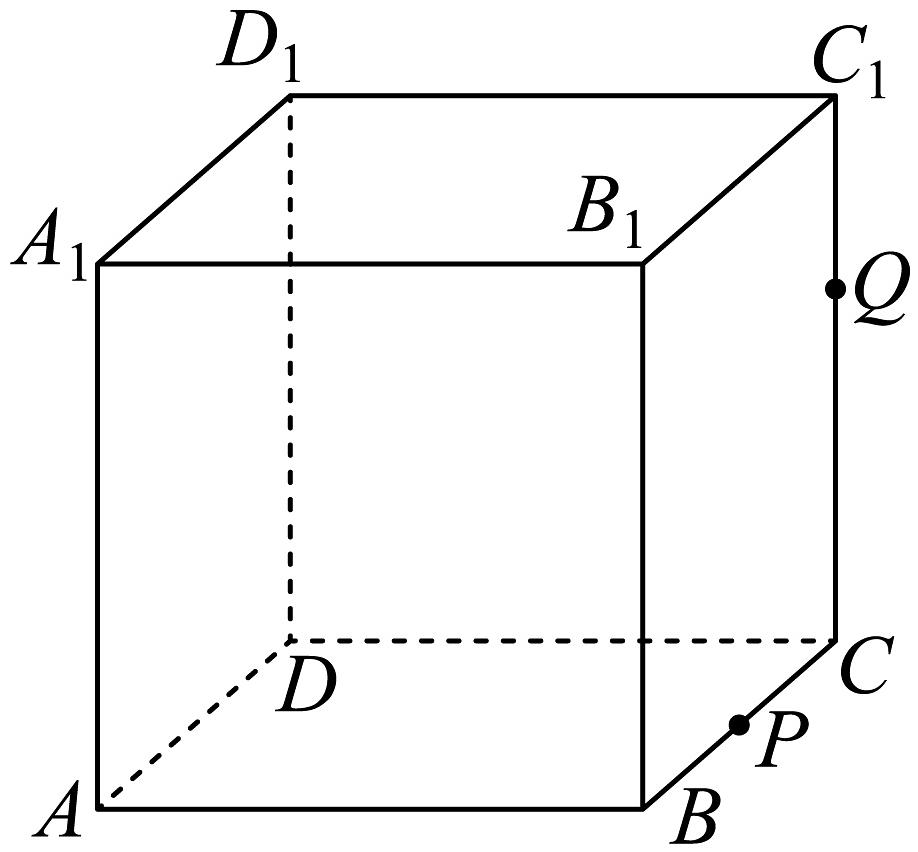 A、直线与直线所成角的正切值为 B、当时,截面S的形状为等腰梯形 C、当时,S与交于点R,则 D、当时,直线与平面的夹角正弦值的取值范围是
A、直线与直线所成角的正切值为 B、当时,截面S的形状为等腰梯形 C、当时,S与交于点R,则 D、当时,直线与平面的夹角正弦值的取值范围是三、填空题:本题共3小题,每小题5分,共15分.
-
12. 某商场为优化服务,对顾客做满意度问卷调查,满意度采用计分制(满分100).现随机抽取了其中10个数据依次为80,85,86,89,91,92,93,95,95,96,则这组数据的第25百分位数为 .13. 在对某中学高一年级学生体重(单位:kg)的调查中,按男、女生人数比例用分层随机抽样的方法抽取部分学生进行测量,已知抽取的男生有50人,其体重的平均数和方差分别为54,20,抽取的女生有40人,其体重的平均数和方差分别为45,11,则估计该校高一年级学生体重的方差为 .
(参考公式:已知总体分为两层,各层的样本量,平均数,方差分别为m, , ;n, , , 记总的样本平均数和样本方差为 , , 其中 .
14. 某封闭的圆锥容器的轴截面为等边三角形,高为6.一个半径为1的小球在该容器内自由运动,则小球能接触到的圆锥容器内壁的最大面积为 .四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
-
15. 如图,正三棱柱中,是的中点, .
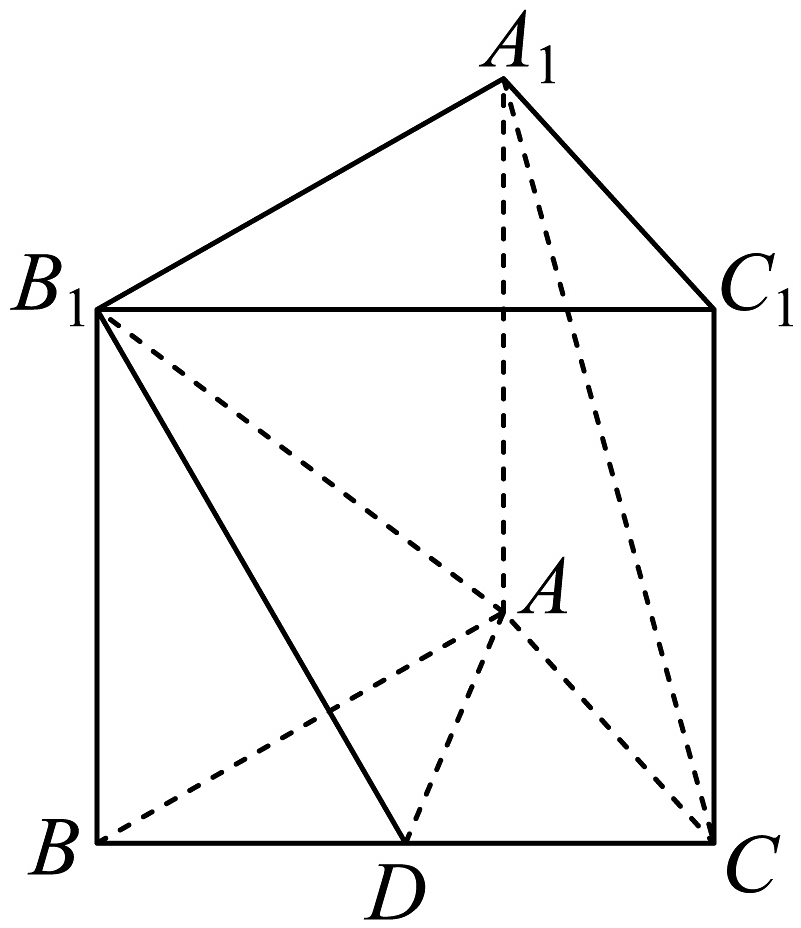 (1)、求证:平面;(2)、若三棱锥的体积为 , 求 .16. 某校对2022年高一上学期期中数学考试成绩(单位:分)进行分析,随机抽取100名学生,将分数按照 , , , , , 分成6组,制成了如图所示的频率分布直方图:
(1)、求证:平面;(2)、若三棱锥的体积为 , 求 .16. 某校对2022年高一上学期期中数学考试成绩(单位:分)进行分析,随机抽取100名学生,将分数按照 , , , , , 分成6组,制成了如图所示的频率分布直方图: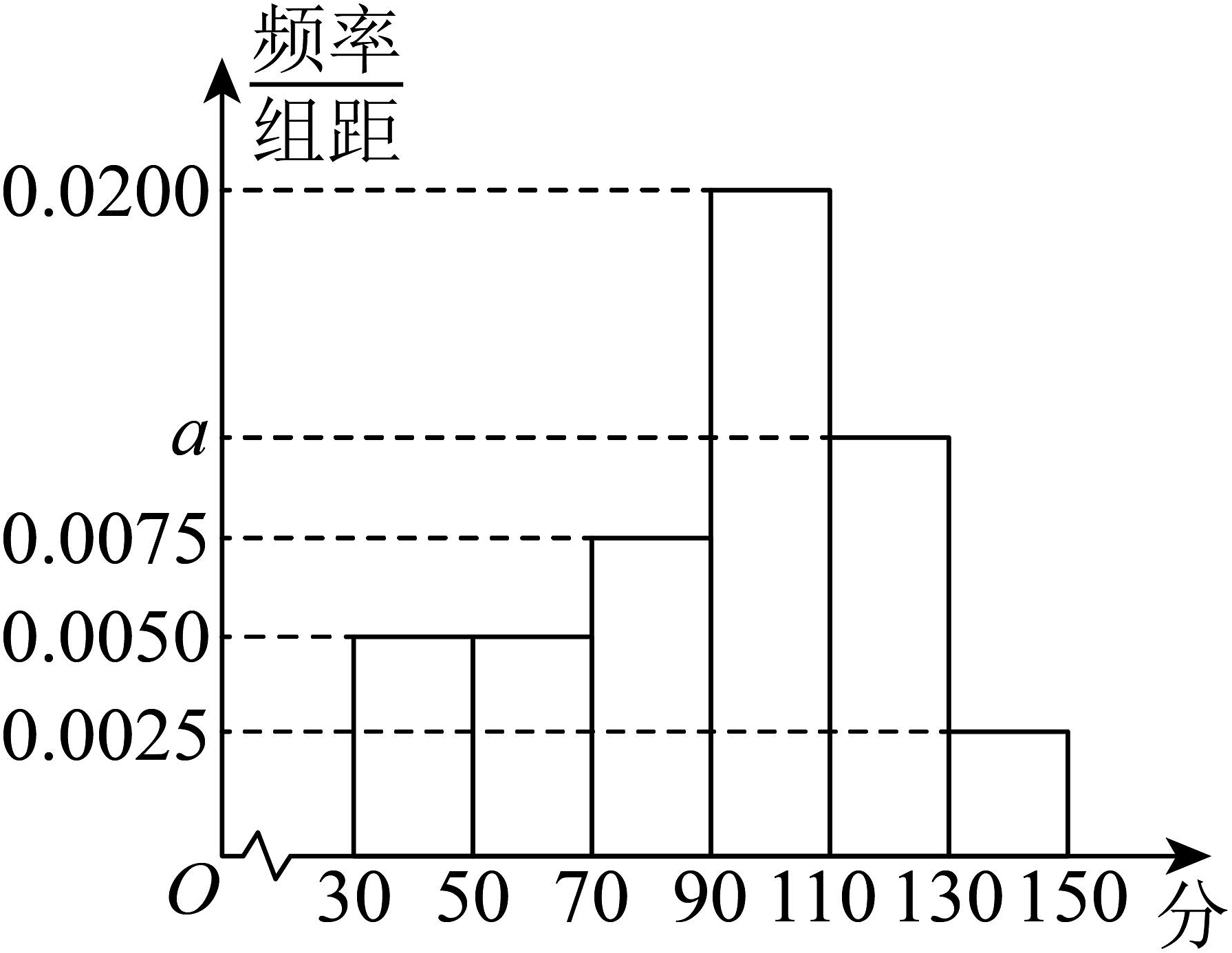
请完成以下问题:
(1)、估计该校高一期中数学考试成绩的平均数;(2)、为了进一步了解学生对数学学习的情况,由频率分布直方图,成绩在和的两组中,用按比例分配的分层随机抽样的方法抽取5名学生,再从这5名学生中随机抽取2名学生进行问卷调查,求抽取的这2名学生至少有1人成绩在内的概率.17. 某校举办环保知识竞赛,初赛中每位参赛者有三次答题机会,每次回答一道题,若答对,则通过初赛,否则直到三次机会用完.已知甲、乙、丙都参加了这次环保知识竞赛,且他们每次答对题目的概率都是 , 假设甲、乙、丙每次答题是相互独立的,且甲、乙、丙的答题结果也是相互独立的.(1)、求甲第二次答题通过初赛的概率;(2)、求乙通过初赛的概率;(3)、求甲、乙、丙三人中恰有两人通过初赛的概率.