浙江省宁波市象山县文峰学校2024-2025学年八年级下学期竞赛数学试卷

试卷更新日期：2025-07-21 类型：竞赛测试

进入出卷网下载

一、选择题（每小题5分，共40分）

1. 在2，5，3，7，2，6，2，1这组数据中插入一个任意数x，则一定不会改变的是（）

A、标准差 B、中位数 C、平均数 D、众数

查看试题解析
2. 已知 $\sqrt{7} = a$ ， $\sqrt{70} = b$ ，则 $\sqrt{4.9}$ 用a，b表示为（）

A、 $\frac{a + b}{10}$ B、 $\frac{a - b}{10}$ C、 $\frac{b}{a}$ D、 $\frac{a b}{10}$

查看试题解析
3. 某工厂第二季度的产值比第一季度的产值增长了x%，第三季度的产值又比第二季度的产值增长了x%，则第三季度的产值比第一季度增长了（）

A、2x% B、1+2x% C、（1+x%）·x% D、（2+x%）·x%

查看试题解析
4. 如图，在□ABCD中，对角线AC与BD相交于点E，∠AEB=45°，BD=4，将△ABC沿直线AC翻折180后与原图形在同一平面内，若点B的落点记为B^' ，则DB'的长为（）

A、 $2 \sqrt{2}$ B、 $2 \sqrt{3}$ C、 $4 \sqrt{2}$ D、 $\sqrt{5}$

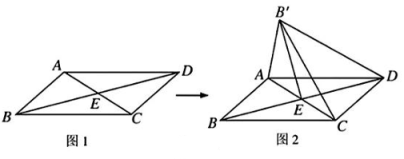查看试题解析
5. 当m，n是实数且满足 $m - n = m n$ 时，就称点Q（m， $\frac{m}{n}$ ）为“奇异点”，已知点A、点B是“奇异点”且都在反比例函数 $y = \frac{2}{x}$ 的图象上，点O是平面直角坐标系原点，则 $△ O A B$ 的面积为（）

A、1 B、 $\frac{3}{2}$ C、2 D、 $\frac{5}{2}$

查看试题解析
6. 如图，矩形ABCD中，E为边AD上一点（不为端点）， $E F ⊥ A D$ 交AC于点F，要求 $△ F B C$ 的面积，只需知道下列哪个三角形的面积即可（）

A、 $△ E B C$ B、 $△ E B F$ C、 $△ E C D$ D、 $△ E F C$

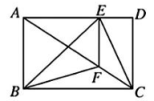查看试题解析
7. 如图，在锐角三角形ABC中，点D，E，F分别是边BC，CA，AB的中点，从每边中点分别作其余两边的垂线，这六条垂线围成六边形DPEQFR，设六边形DPEQFR的面积为 $S_{1}$ ， $△ A B C$ 的面积为S，则 $S_{1} : S =$ （）

A、3：5 B、2：3 C、1：2 D、1：3

查看试题解析
8. 如图，在平面直角坐标系中，矩形ABCD的对角线AC的中点与坐标原点重合，点E是x轴上一点，连结AE.若AD平分∠OAE，反比例函数y= $\frac{k}{x}$ （k>0，x>0）的图象经过AE上的两点A，F，且AF=EF，△ABE的面积为18，则k的值为（）

A、6 B、12 C、18 D、24

查看试题解析

二、填空题（每小题5分，共30分）

9. 若 $\sqrt{189 n}$ 是正整数，则整数n的最小值为.

查看试题解析
10. 已知a是方程 $x^{2} + x - 1 = 0$ 的一个根，则 $\frac{2}{a^{2} - 1} - \frac{1}{a^{2} - a}$ 的值为.

查看试题解析
11. 若关于 $x$ 的不等式组 ${\begin{cases} 5 - 2 x > 0, \\ 3 x + a \geq 0 \end{cases}$ 无实数解，则 $a$ 的取值范围是

查看试题解析
12. 如图，①②③④⑤五个平行四边形拼成一个含30内角的菱形EFGH（不重叠无缝隙）.若①②③④四个平行四边形面积的和为14cm² ，四边形ABCD面积是11cm² ，则①②③④四个平行四边形周长的总和为.

查看试题解析
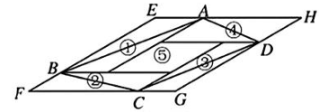13. 如图所示，以 $R t △ A B C$ 的斜边BC为一边在 $△ A B C$ 的同侧作正方形BCEF，设正方形的中心为O，连AO，如果 $A B = 4$ ， $A O = 6 \sqrt{2}$ ，那么 $S_{△ A O B} =$ .

查看试题解析
14. 如图，在平面直角坐标系中，已知直线 $y = k x (k > 0)$ 分别交反比例函数 $y = \frac{4}{x}$ 和 $y = \frac{9}{x}$ 在第一象限的图于点A，B，过点B作BD⊥x轴于点D，交 $y = \frac{4}{x}$ 的图象于点C，连接AC.若 $△ A B C$ 是等腰三角形，则k的值是.

查看试题解析

三、解答题（共4小题，共55分）

15. 已知方程 $x^{2} + p x + q = 0$ 的两个根是 $x_{1}$ ， $x_{2}$ ，那么 $x_{1} + x_{2} = - p$ ， $x_{1} x_{2} = q$ ，反过来，如果 $x_{1} + x_{2} = - p$ ， $x_{1} x_{2} = q$ ，那么以 $x_{1}$ ， $x_{2}$ 为两根的一元二次方程是 $x^{2} + p x + q = 0$ .请根据以上结论，解决下列问题：

(1)、已知关于x的方程 $x^{2} + m x + n = 0 (n \neq 0)$ ，求出一个一元二次方程，使它的两根分别是已知方程两根的倒数.

(2)、已知a，b满足 $a^{2} - 15 a - 5 = 0$ ， $b^{2} - 15 b - 5 = 0$ ，求 $\frac{a}{b} + \frac{b}{a}$ 的值.

(3)、已知a，b，c均为实数，且 $a + b + c = 0$ ， $a b c = 16$ ，求正数c的最小值.

查看试题解析
16. 如图1，在平面直角坐标系xOy中，点F（2，2），过函数 $y = \frac{k}{x} (x > 0,$ 常数k>0）图象上一点A（ $\frac{1}{2}$ ， a）作y轴的平行线交直线l：y=-x+2于点C，且AC=AF.

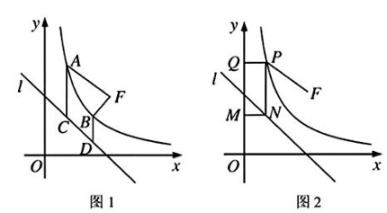(1)、求a的值，并写出函数 $y = \frac{k}{x} (x > 0)$ 的解析式；

(2)、过函数 $y = \frac{k}{x} (x > 0)$ 图象上任意一点B，作y轴的平行线交直线l于点D，是否总有BD=BF成立？并说明理由；

(3)、如图2，若P是函数 $y = \frac{k}{x} (x > 0)$ 图象上的动点，过点P作x轴的垂线交直线l于点N，分别过点P、N作y轴的垂线交y轴于点Q、M，问：是否存在点P，使得矩形PQMN的周长取得最小值？若存在，请求出此时点P的坐标及矩形PQMN的周长；若不存在，请说明理由.

查看试题解析
17. 如图，在菱形ABCD中，∠A=60°AB=4，E是AD边上的动点，作∠BEF=60咬CD于点F，在AB上取点G使AG=AE，连结EG.

(1)、求∠EGB的度数：

(2)、求证：EF=BE：

(3)、若P是EF的中点，当AE为何值时，△EGP是等腰三角形.

查看试题解析
18. 定义：我们把对角线长度相等的四边形叫做等线四边形．

(1)、尝试：如图1，在3×3的正方形网格图形中，已知点A、点B是两个格点，请你作出一个等线四边形，要求A、B是其中两个顶点，且另外两个顶点也是格点；

(2)、推理：如图2，已知△AOD与△BOC均为等腰直角三角形，∠AOD＝∠BOC＝90°，连结AB，CD，求证：四边形ABCD是等线四边形；

(3)、拓展：如图3，已知四边形ABCD是等线四边形，对角线AC，BD交于点O，若∠AOD＝60°，AB＝ $\sqrt{7}$ ，BC＝ $\sqrt{3}$ ，AD＝2．求CD的长．

查看试题解析