浙江省宁波市储能中学2024-2025学年九年级上学期12月“储能杯”数学竞赛试卷

试卷更新日期：2025-07-21 类型：竞赛测试

进入出卷网下载

1. 在 $△ A B C$ 中， $s i n A =$ $\frac{2}{3}$ ，则 $∠ A$ 的范围为 ( )

A、 $0^{\circ} < A < 30^{\circ}$ B、 $30^{\circ} < A < 45^{\circ}$ C、 $45^{\circ} < A < 60^{\circ}$ D、 $60^{\circ} < A < 90^{\circ}$

查看试题解析
2. 化简 $\sqrt{9 - 4 \sqrt{5}} =$ ( )

A、 $\sqrt{5} - \sqrt{3}$ B、 $\sqrt{5} - 2$ C、 $3 - \sqrt{7}$ D、 $\sqrt{7} - 3$

查看试题解析
3. 已知 $(x^{2} - 1) (x^{2} - 4) = K$ 有四个非零实数根，且在数轴上对应的四个点等距排列，则 $K$ 的值为 ( )

A、 $\frac{3}{4}$ B、 $\frac{5}{4}$ C、 $\frac{7}{4}$ D、 $\frac{9}{4}$

查看试题解析
4. $X, Y$ 均为整数， ${(X^{2} + X + 1)}^{2} + {(Y^{2} + Y + 1)}^{2}$ 为完全平方数，则(X， Y)有几组 ( )

A、0 B、1 C、无数组 D、以上都不对

查看试题解析
5. $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}, a_{7}$ 是 $1 、 2 、 3 、 4 、 5 、 6 、 7$ 的一个任意排序数列，令 $S = a_{1} a_{2} + a_{2} a_{3} + a_{3} a_{4} + a_{4} a_{5} + a_{5} a_{6} + a_{6} a_{7} + a_{7} a_{1}$ ，则 $S$ 的最小值为 ( )

A、84 B、85 C、86 D、87

查看试题解析

6. 令 $x = \sqrt{3} - 1$ ，则 $2 x^{2} + \frac{4}{x^{2}} + 2 x + 1 =$ .

查看试题解析
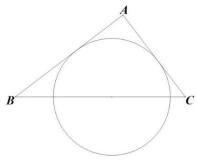
7. 小明有六件工艺品，四件正品，两件次品，小明对其进行逐一检查，检查次数小于等于三次的概率.

查看试题解析
8. 如图， $△ A B C$ 是直角三角形， $A B = 4, A C = 3$ ，三角形内有一圆且圆心在斜边 $B C$ 上，圆与 $A B, A C$ 相切，则圆的半径 $r =$ .

查看试题解析
9. 现有数列 $1, 2, 2, 3, 3, 3, 4, 4, 4, 4, \dots \dots$ ，则第 2024 项除以 5 的余数是.

查看试题解析
10. 已知 $x = \sqrt{x - \frac{1}{x}} + \sqrt{1 - \frac{1}{x}}$ ，则 $x =$ .

查看试题解析
11. 如图，在 $△ A B C$ 中， $\frac{B D}{C D} = p, \frac{C E}{A E} = q, \frac{A F}{B F} = r$ ，则 $\frac{S_{△ P Q R}}{S_{△ A B C}} =$ .

查看试题解析

12. 现有 $x, y, z$ 三个正整数， $\frac{x (y + 1)}{x - 1}, \frac{y (z + 1)}{y - 1}, \frac{z (x + 1)}{z - 1}$ 均为正整数，求 $x y z$ 的最大值与最小值之和.

查看试题解析
13. 已知 $f (x) = x^{n} + a x + b$ ，满足 $f (1) = 8, f (- 1)$ $= 0, f (2) = 18, f (3) = 40$ .

(1)、求 $f (x)$ ；

(2)、对于任意整数 $x$ ，使得 $f (x) \geq k (x^{2} + x)$ 恒成立，求 $k$ 的最大值.

查看试题解析
14. 是否存在正整数 $a, b, c$ 满足 $(a + b + c) (a + b - c)$ $(b + c - a) (c + a - b) = 24$ . 若存在请求出值；若不存在请说明理由.

查看试题解析
15. 如图，在四边形 $A B C D$ 中， $∠ C A B = ∠ C A D, ∠ A B C$ $= ∠ A C D, A E ⊥ B C$ 于 $E, A F ⊥ C D$ 于 $F, H$ 为 $△ A E F$ 的垂心，求证： $D 、 H 、 B$ 三点共线.

查看试题解析