广东省深圳市罗湖区深圳中学2024-2025学年七年级下学期期末考试数学试题

试卷更新日期：2025-07-21 类型：期末考试

进入出卷网下载

一、选择题 (本大题共8小题，每小题3分，共24分)

1. 博物馆是保护和传承人类文明的重要场所.下列博物馆标志中，文字上方的图案不是轴对称图形的是( )

A、 B、 C、 D、

查看试题解析
2. 引力常量G是物理学中最基础但也最难精确测量的常数之一，我国华中科技大学引力中心团队于2018年得到了目前最精确的引力常量G的值，精确度达到11.6 ppm (即0.0000116). 数据0.0000116可用科学记数法表示为( )

A、-1.16×10⁵ B、-11.6×10⁶ C、 $1.16 \times 1 0^{- 5}$ D、 $11.6 \times 1 0^{- 6}$

查看试题解析
3. 下列运算正确的是( )

A、 $x^{2} \cdot x^{6} = x^{8}$ B、 ${(2 x y)}^{2} = 2 x^{2} y^{2}$ C、 ${(x - y)}^{2} = x^{2} - y^{2}$ D、 ${(x^{3})}^{4} = x^{7}$

查看试题解析
4. 学校图书馆随机选取部分初一学生进行了问卷调查，了解大家“最喜爱的图书类别”，调查共收到500份问卷，结果统计如下表：
最喜爱的图书类别
科学
文学
历史
其他
人数
130
150
120
100
若随机挑选该校一名初一学生，则该生最喜欢“文学类”图书的概率约为( )

A、 $\frac{1}{5}$ B、 $\frac{6}{25}$ C、 $\frac{13}{50}$ D、 $\frac{3}{10}$

查看试题解析
5. 如图，由下列条件能得到 l₁//l₂的是（）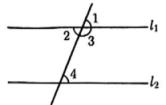

A、∠1=∠2 B、∠1=∠4 C、∠3=∠4 D、∠2+∠4=180

查看试题解析
6. 小深在周末进行骑行训练.他从家出发，以10 km/h的速度匀速骑行，用时x小时骑行y千米. 下列说法正确的是( )

A、10和x是常量，y是变量 B、10是常量，x和y是变量 C、10和y是常量，x是变量 D、以上说法均错误

查看试题解析
7. 如图，在△ABC中， BC =12，∠ACB =45°. 以B为圆心，适当长为半径画圆弧，分别交BA，BC于M和N，再分别以M和N为圆心，大于 $\frac{1}{2} M N$ 的长为半径画圆弧，两弧交于 P. 射线BP交AC于D. DE⊥AB，垂足为E； DF⊥BC，垂足为F. 若DE=4，则BF的长为( )

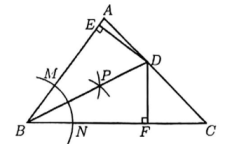A、4 B、6 C、8 D、10

查看试题解析
8. 如图， △ABC为等边三角形， △ADE 为等腰三角形，其中∠AED =120°，AE = DE，且 B，C，D在同一直线上. 连接BE和CE.则以下结论中正确的个数为(    )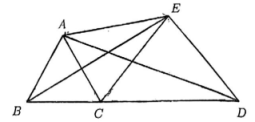
①∠BAE+∠CDE=180°；        ② BE为∠ABC的平分线；
③ AE =CE；        ④∠ECD = 60°.

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题 (本大题共5小题，每小题3分，共15分)

9. 10张卡片编号依次为1，2，⋯，10，且除编号以外这些卡片无任何差别.随机抽取一张卡片，抽到编号为3的倍数的卡片的概率是.

查看试题解析
10. 如图，在△ABC中，AB=AC，D在BA延长线上， $∠ D A C = 14 0^{\circ} ，$ 则 $∠ B =$ °.

查看试题解析
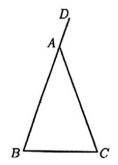11. 如图，在△ABC中，BC=6， D为BC边上一点， $A D ⟂ B C ， △ A B C$ 的面积为15，则A到直线BC的距离为.

查看试题解析
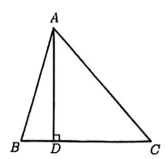12. 小圳从A 地出发，匀速向B 地步行.小圳与B 地的距离y(米)与步行时间x(分钟)的关系如下表：
x(分钟)
0
1
2
3
y(米)
960
880
800
720
由表格中y与x关系可知，当步行分钟后，小圳走完全程的一半.

查看试题解析
13. 两个全等的三角形按如图方式摆放，其中 $∠ A B C = 9 0^{\circ} ， ∠ B A C = x^{\circ} ， A B =$ 5，BC=2，△ABC≌△DEF. 此时B，E重合， B，C，D在同一直线上. 现将△DEF 沿射线BC向右平移.在平移过程中，直线AB 与DF交于点G，∠CAG的平分线与直线EF交于点H，则∠AHE=°(用含x的代数式表示).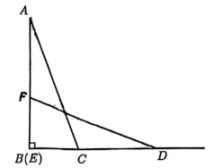

查看试题解析

三、解答题 (本大题共7小题，共61分)

14. 计算：

(1)、 ${(\frac{2}{3})}^{- 1} - π^{0} + ∣ - 1 - \frac{1}{2} ∣ - {(- 1)}^{2028};$

(2)、 $1 + 2 \times 44 + 4 4^{2}$ (用简便方法计算).

查看试题解析
15. 先化简，再求值： $(2 a + b) (2 a - b) + (2 a b^{2} - 8 a^{2} + 2 a) \div 2 a$ 其中a=1，b=-1.

查看试题解析
16. 盒子中装有8个红球，9个白球和若干个黑球，除颜色以外这些球无任何差别.随机从盒中摸一个球，已知摸到红球的概率为 $\frac{1}{3}$

(1)、摸到黄球是(从“随机事件”，“必然事件”，和“不可能事件”中选一个填空)；

(2)、求盒中黑球的个数；

(3)、若往盒中再加入若干个红球，使摸到黑球的概率为 $\frac{1}{4} ，$ 求加入的红球个数.

查看试题解析
17. 如图，在每个小正方形的边长均为1个单位长度的网格中，△ABC的三个顶点都在其格点上.

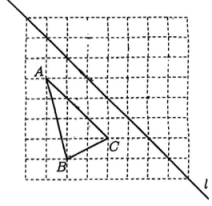(1)、 △ABC 的面积为.

(2)、画出△ABC关于直线l的轴对称图形 $△ A_{1} B_{1} C_{1};$

(3)、在直线l上求作一点P，使PB+PA值最小(保留作图痕迹，不写作法).

查看试题解析
18. 如图，在 $△ A B C$ 中， $∠ A = 9 0^{\circ} ，$ D为AB边上一点， $∠ C D A$ 的角平分线交AC于E，且 $D E ‖ B C .$ F为BC的中点.

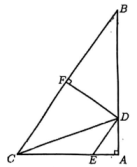(1)、求证： DF⊥BC；

(2)、若 $A B = 10 ， A C = 7 ，$ 求△ACD的周长.

查看试题解析

19. 项目式学习

项目主题：深圳地铁票价探究
素材1	深圳地铁实行里程分段计价票制.普通车厢起步价：首4公里人民币2元；4公里至12公里部分，每人民币1元可乘坐4公里；12公里至24公里部分，每人民币1元可乘坐6公里；超过24公里，每人民币1元可乘坐8公里. 备注：两个地铁站之间里程为两站之间沿地铁的最短线路长度.例如，若某两站之间有两种乘坐线路，长度分别为4公里和4.1公里，则此两站之间的里程为4公里，票价为2元.
素材2	深圳地铁的部分线路图如下(经过变形处理，并省略部分站点)，标注了部分站点之间的地铁线路及里程.
素材3	深圳市深圳通有限公司与手机公司合作推出深圳通互联互通卡业务，该卡是通过NFC芯片绑定在手机上的一张虚拟公交卡.手机用户支付 16元不可退服务费用后办理此卡后，可在乘坐地铁普通车厢使用此卡刷卡出闸时享受票价9.5折优惠.
问题解决
⑴任务1	小达乘坐地铁从A站到B站，票价为3元，则A、B两站之间的最长里程为 ▲ km.
⑵任务2	小达从布心站出发，乘坐5号线前往临海站并出站游玩，游玩后再从临海站出发，依次乘坐5号线、11号线、14号线、7号线和5号线回到布心站，求全程的地铁票价.
⑶任务3	小达以任务2的方式在布心站和临海站之间往返，设其往返的来回数为x，办理深圳通互联互通卡出行相比不办理节省的费用为y，请求出y与x的关系式，并计算至少往返几个来回时，办理深圳通互联互通卡出行比不办理更划算?

查看试题解析

20. 综合与实践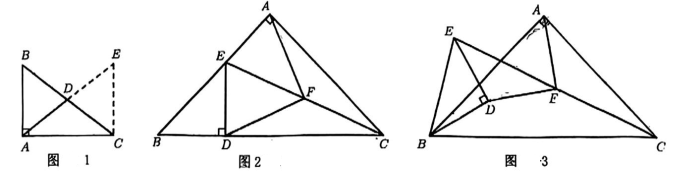

(1)、【阅读理解】如图1，在Rt△ABC中， ∠BAC = 90°， D为斜边BC 上的中点.为了探究中线AD与斜边BC的数量关系，某数学小组经过合作探究，猜想 $A D = \frac{1}{2} B C .$ 为了证明这一猜想，他们采用了“倍长中线法”，即将中线AD延长到E，使得AD =DE，连接CE.据此将他们的证明过程补充完整.
证明：∵D为BC的中点
∴BD=CD
在△ABD与△ECD中，
${\begin{cases} B D = C D \\ ∠ A D B = ∠ E D C, \\ A D = D E \end{cases}$
∴△ABD≌△ECD (① ▲   )
∴AB =CE，∠ABD =∠ECD
∴(②    ▲    //    ▲    )
∴∠BAC+∠ECA= 180°(③   ▲   )
∵ $∠ B A C = 9 0^{\circ}$
∴∠ECA=∠BAC=90°
在△ABC与△CEA中，
${\begin{cases} A B = C E \\ ∠ B A C = ∠ E C A, \\ A C = A C \end{cases}$
∴△ABC≌△CEA(SAS)
∴BC=AE (④ ▲   )
∴ $A D = \frac{1}{2} A E = \frac{1}{2} B C$

(2)、【深入探究】如图2， △ABC 和△EBD 为等腰直角三角形， ∠BAC=∠BDE=90°， AB =AC， BD =DE. 若点D 在线段BC上，连接EC， F 为线段EC 的中点，连接AF和DF.猜想AF和DF的数量、位置关系，并说明理由.

(3)、【拓展应用】如图3，将(2)中条件改为点D 是△ABC 内一点，其余不变.问(2)中的结论仍成立吗?若成立，请证明；若不成立，请说明理由.

查看试题解析

最喜爱的图书类别	科学	文学	历史	其他
人数	130	150	120	100

x(分钟)	0	1	2	3
y(米)	960	880	800	720