湖南省长沙市第一中学2025届高三下学期模拟（二）数学试题

试卷更新日期：2025-06-01 类型：高考模拟

进入出卷网下载

一、选择题（本大题共8个小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)

1. 已知集合 $A = \{x ∣ 0 \leq x \leq a\} ， B = \{x ∣ x^{2} - 2 x \leq 0\}$ ，若 $B \subseteq A$ ，则实数 $a$ 的取值范围是（）

A、 $(0, 2)$ B、 $(0, 2]$ C、 $(2, + \infty)$ D、 $[2, + \infty)$

查看试题解析
2. 若 $(z - i^{2024}) i = i^{5} + i^{6}$ ，则 $\bar{z}$ 的虚部为（）

A、 $- 1$ B、1 C、 $- i$ D、i

查看试题解析
3. 平面上的三个力 $F_{1}$ ， $F_{2}$ ， $F_{3}$ 作用于同一点，且处于平衡状态.已知 $\vec{F_{1}} = (1, 0)$ ， $|\vec{F_{2}}| = 2$ ， $⟨\vec{F_{1}}, \vec{F_{2}}⟩ = 120^{\circ}$ ，则 $|\vec{F_{3}}| =$ （　　）

A、 $\frac{1}{2}$ B、1 C、 $\sqrt{3}$ D、2

查看试题解析
4. 国际学生评估项目测试是世界经济合作与发展组织对各国中学生阅读、数学、科学能力评价测试．从 $2000$ 年开始，每 $3$ 年进行一次测试评估．在评估研究时将测试成绩按一定规则转换成等级赋分，赋分范围是 $40$ 至 $100$ 分，如图是 $2024$ 年的某地中学生参加阅读测试后用赋分数据绘制成的不完整频率分布直方图．根据图中数据，下面说法正确的是（）

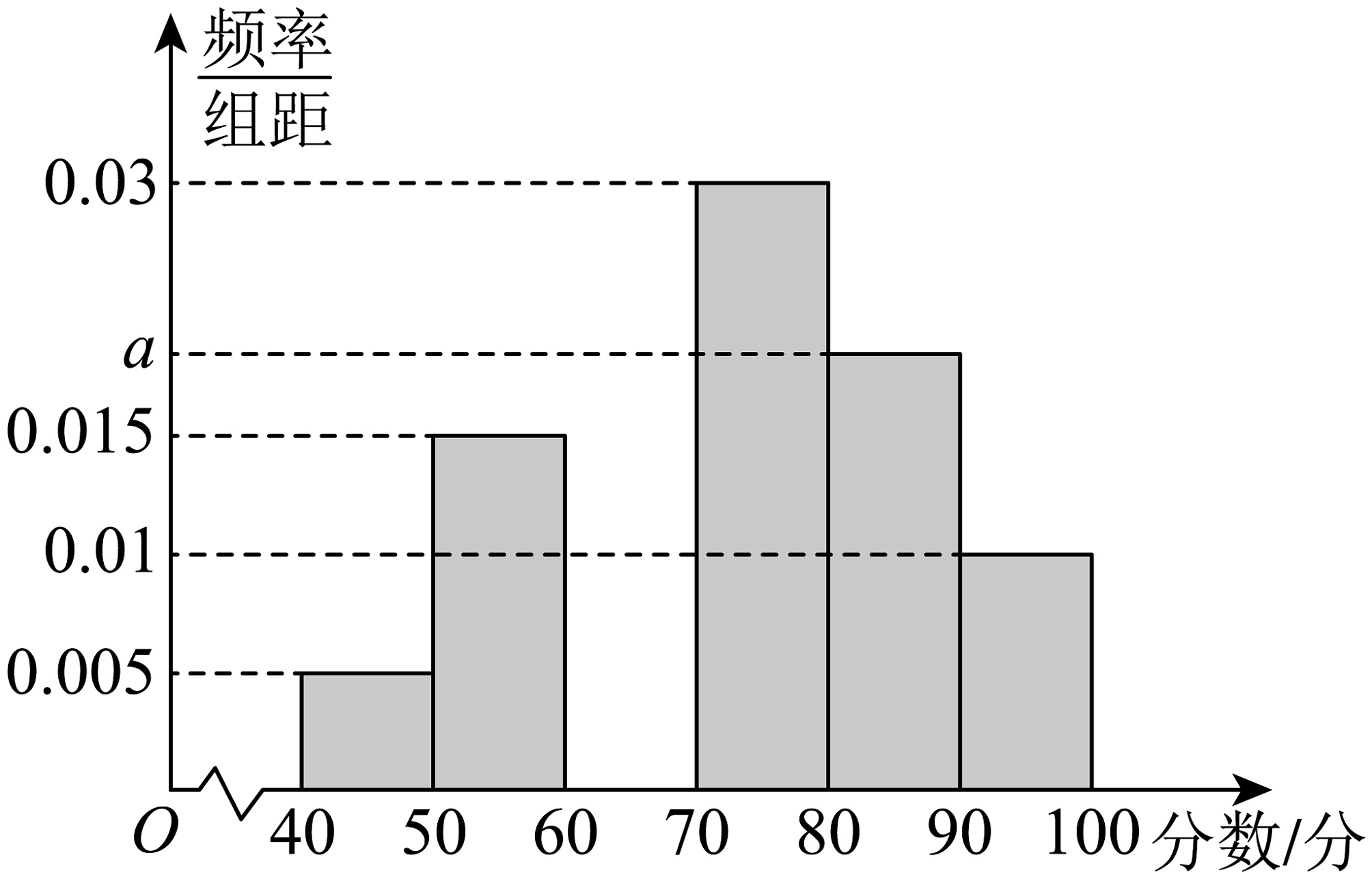A、该地学生成绩的中位数一定大于 $75$ B、该地学生成绩的平均数一定小于 $65$ C、该地学生成绩的极差介于 $40$ 至 $60$ 之间 D、该地学生成绩没有超过 $60$ 分的学生所占比例为 $30 %$

查看试题解析
5. 六名同学排成一排照相，则其中甲､乙､丙三人两两不相邻，且甲和丁相邻的概率为（）

A、 $\frac{2}{5}$ B、 $\frac{1}{5}$ C、 $\frac{2}{15}$ D、 $\frac{1}{10}$

查看试题解析
6. 已知 $α \in (\frac{π}{2} ， π)$ ，且 $3 c o s 2 α - s i n α = 2$ ，则（）

A、 $c o s (π - α) = \frac{2}{3}$ B、 $t a n (π - α) = \frac{\sqrt{2}}{4}$ C、 $s i n (\frac{π}{2} - α) = \frac{\sqrt{5}}{3}$ D、 $c o s (\frac{π}{2} - α) = \frac{\sqrt{5}}{4}$

查看试题解析
7. 已知函数 $f (x) = \frac{|2^{x - 1} - 1| + 2^{x - 1} + 1}{2}$ ，若 $f (m^{2} - m - 1) > f (- m^{2})$ ，则实数 $m$ 的取值范围（）

A、 $(- \frac{1}{2}, 1)$ B、 $(- 1, 2)$ C、 $(- \infty, - \frac{1}{2}) \cup (1, + \infty)$ D、 $(- \infty, - 1) \cup (2, + \infty)$

查看试题解析
8. 在同一平面直角坐标系内，函数 $y = f (x)$ 及其导函数 $y = f^{'} (x)$ 的图象如图所示，已知两图象有且仅有一个公共点，其坐标为 $(0, 1)$ ，则（）

A、函数 $y = f (x) \cdot e^{x}$ 的最大值为1 B、函数 $y = f (x) \cdot e^{x}$ 的最小值为1 C、函数 $y = \frac{f (x)}{e^{x}}$ 的最大值为1 D、函数 $y = \frac{f (x)}{e^{x}}$ 的最小值为1

查看试题解析

二、选择题（本大题共3小题，每小题6分，共18分．在每小题给出的选项中，至少有两项符合题目要求，若全部选对得6分，部分选对得部分分，选错或不选得0分)

9. 已知函数 $f (x) = sin(2 x - \frac{π}{6})$ ，则（）

A、 $f (x)$ 的最小正周期为 $π$ B、 $f (x)$ 的图象关于直线 $x = \frac{π}{12}$ 对称 C、 $f (x)$ 在 $(\frac{π}{3}, \frac{5 π}{6})$ 上单调递减 D、 $f (x)$ 在 $(0, π)$ 上有2个零点

查看试题解析
10. 已知A，B，C是抛物线 $W : y^{2} = 28 x$ 上不同的动点，F为抛物线W的焦点，直线l为抛物线W的准线，AB的中点为 $P (m, n)$ ，则（）

A、当 $m = 9$ 时， $|A B|$ 的最大值为32 B、当 $m = 8$ 时， $|C P| + |C F|$ 的最小值为22 C、当 $n = 5$ 时，直线AB的斜率为 $\frac{14}{5}$ D、当 $\vec{A F} // \vec{A B}$ 时，点P到直线l的距离的最小值为14

查看试题解析
11. 已知函数 $f (x) = sin x - ln x, f^{'} (x)$ 是其导函数.若存在 $x_{1}, x_{2} \in (0, π)$ 且 $x_{1} < x_{2}$ ，满足 $f^{'} (x_{1}) = f^{'} (x_{2})$ ，则（）

A、 $f (x_{1}) > f (x_{2})$ B、 $x_{1} x_{2} > 1$ C、 $f (x_{1}) f (x_{2}) > 1$ D、 $f (x_{1}) + f (x_{2}) < 2$

查看试题解析

三、填空题（本大题共3个小题，每小题5分，共15分）

12. 已知数列 $\{a_{n}\}$ .的前 $n$ 项和为 $S_{n}$ ，且 $a_{n + 2} + a_{n} - 2 a_{n + 1} = 0 (n \in N^{*})$ .若 $a_{11} + a_{15} + a_{19} = 12$ ，则 $S_{29} =$ .

查看试题解析
13. 某校象棋社团开展竞赛活动，比赛中双方有一人获胜或者双方和棋则比赛结束.根据以往比赛结果，在一局比赛中，甲战胜乙的概率是 $\frac{1}{2}$ ，两人和棋的概率是 $\frac{1}{6}$ ，则乙战胜甲的概率是；甲乙两人比赛2局，每局胜方记3分，负方记0分，和棋双方各记1分，则甲得分不少于2分的概率是.

查看试题解析
14. 已知正四面体 $A B C D$ 的棱长为 $2 \sqrt{2}$ ，动点P满足 $P A^{2} + P B^{2} = P C^{2} + P D^{2}$ ，用所有这样的点P构成的平面截正四面体，则所得截面的面积为.

查看试题解析

四、解答题（本大题共5个小题，共77分．解答应写出文字说明、证明过程或演算步骤）

15. 在 $△ A B C$ 中，内角 $A, B, C$ 的对边分别为 $a, b, c$ ，且满足 $sin A (sin A - sin C) = {sin}^{2} (A + C) - {sin}^{2} C$ .

(1)、求 $B$ ；

(2)、若 $P$ 为边 $A C$ 上一点（异于端点）， $∠ B P C = 2 ∠ A$ ，求 $\frac{|A P|}{|P C|}$ 的取值范围.

查看试题解析
16. 一个不透明的盒子中装有规格完全相同的3个小球，标号分别为 $1, 2, 3$ ，现采用有放回的方式摸球两次，每次摸出1个小球，记第一次摸到的小球号码为 $i$ ，第二次摸到的小球号码为 $j$ .

(1)、记“ $i + j > i \cdot j$ ”为事件 $A$ ，求 $P (A)$ ；

(2)、完成两次摸球后，再将与前面3个球规格相同的4号球和5号球放入盒中，并进行第三次摸球，且将第三次摸到的小球号码记为 $k$ ，号码 $i, j, k$ 中出现偶数的个数记为 $X$ ，求 $X$ 的分布列及数学期望.

查看试题解析
17. 已知圆 $C_{1} : x^{2} + y^{2} = 1 ， O$ 为坐标原点，过 $C_{1}$ 上任意一点 $P (x_{0} ， y_{0}) (x_{0} \cdot y_{0} \neq 0)$ 作圆 $C_{1}$ 的切线 $l$ .

(1)、若 $l$ 与椭圆 $C_{2} : \frac{x^{2}}{4} + \frac{3 y^{2}}{4} = 1$ 相交于 $A, B$ 两点，证明： $O A ⊥ O B$ ；

(2)、若 $l$ 与椭圆 $C_{2} : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ 相交于 $A, B$ 两点，恒有 $O A ⊥ O B$ ，判断 $C_{2}$ 是否过定点？请说明理由.

查看试题解析
18. 已知函数 $f (x) = (x - 2) e^{x - 1} - a x^{2} + 2 a x$ ．

(1)、当 $a = e$ 时，求 $f (x)$ 的单调性；

(2)、若函数 $f (x)$ 在 $x = 1$ 处取得极小值，求实数 $a$ 的取值范围．

查看试题解析
19. 已知四面体 $A B C D$ .

(1)、若该四面体为正四面体，球 $O$ 与其四个面都相切，证明：该四面体与球 $O$ 的体积之比等于它们的表面积之比；

(2)、设点 $G$ 是满足 $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = \vec{0}$ ，过点 $G$ 的平面 $Ω$ 分别与直线 $A B$ ， $A C$ ， $A D$ 交于点 $P$ ， $Q$ ， $R$ ，且 $\vec{A P} = λ_{1} \vec{A B}$ ， $\vec{A Q} = λ_{2} \vec{A C}$ ， $\vec{A R} = λ_{3} \vec{A D}$ ，证明： $\frac{1}{λ_{1}} + \frac{1}{λ_{2}} + \frac{1}{λ_{3}} = 4$ ；

(3)、若空间内一点 $H$ 满足 $a \vec{H A} + b \vec{H B} + c \vec{H C} + d \vec{H D} = \vec{0}$ （ $a$ ， $b$ ， $c$ ， $d$ 均为实数，且全不为0），证明： $V_{H - B C D} : V_{H - A C D} : V_{H - A B D} : V_{H - A B C} = |a| : |b| : |c| : |d|$ .

查看试题解析