广东省茂名市高州市2025届高三高考适应性考试数学试卷
试卷更新日期:2025-05-23 类型:高考模拟
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 随机变量 , 若 , 则实数的值为( )A、2 B、 C、3 D、43. 已知圆 , 直线 , 若圆上有且仅有一点到直线的距离为1,则( )A、2 B、 C、±2 D、4. 已知向量 , , 且在方向上的投影向量为 , 则( )A、 B、 C、 D、5. 若 , 则( )A、 B、 C、 D、6. 已知函数 , 若 , 则的取值范围是( )A、 B、 C、 D、7. 已知圆锥的母线长为定值,则该圆锥的体积最大时,其母线与底面所成的角的余弦值为( )A、 B、 C、 D、8. 已知函数满足 , , 设 , 为数列的前项和,则使得成立的最小整数为( )A、8 B、9 C、10 D、11
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
-
9. 已知为关于的方程在复数范围内的一个根,则( )A、 B、 C、为纯虚数 D、为关于的方程的另一个根10. 已知随机事件 , 满足 , , 则下列说法正确的是( )A、若 , 相互独立,则 B、若 , 相互独立,则 C、若 , 则 D、若 , 则11. 抛物线的光学性质是指平行于抛物线对称轴的光线通过反射后经过抛物线的焦点.且光线反射遵循反射基本定理,反射点处的切线与入射光线反射光线所成夹角的角平分线垂直.如图,已知抛物线 , 一束光线从点出发平行于轴射入抛物线,经过两次反射后平行射出,轴,设反射点分别为 , , 为坐标原点,过 , 分别作 , 的角平分线交于点 , 已知的最小值为2,则下列说法正确的是( )
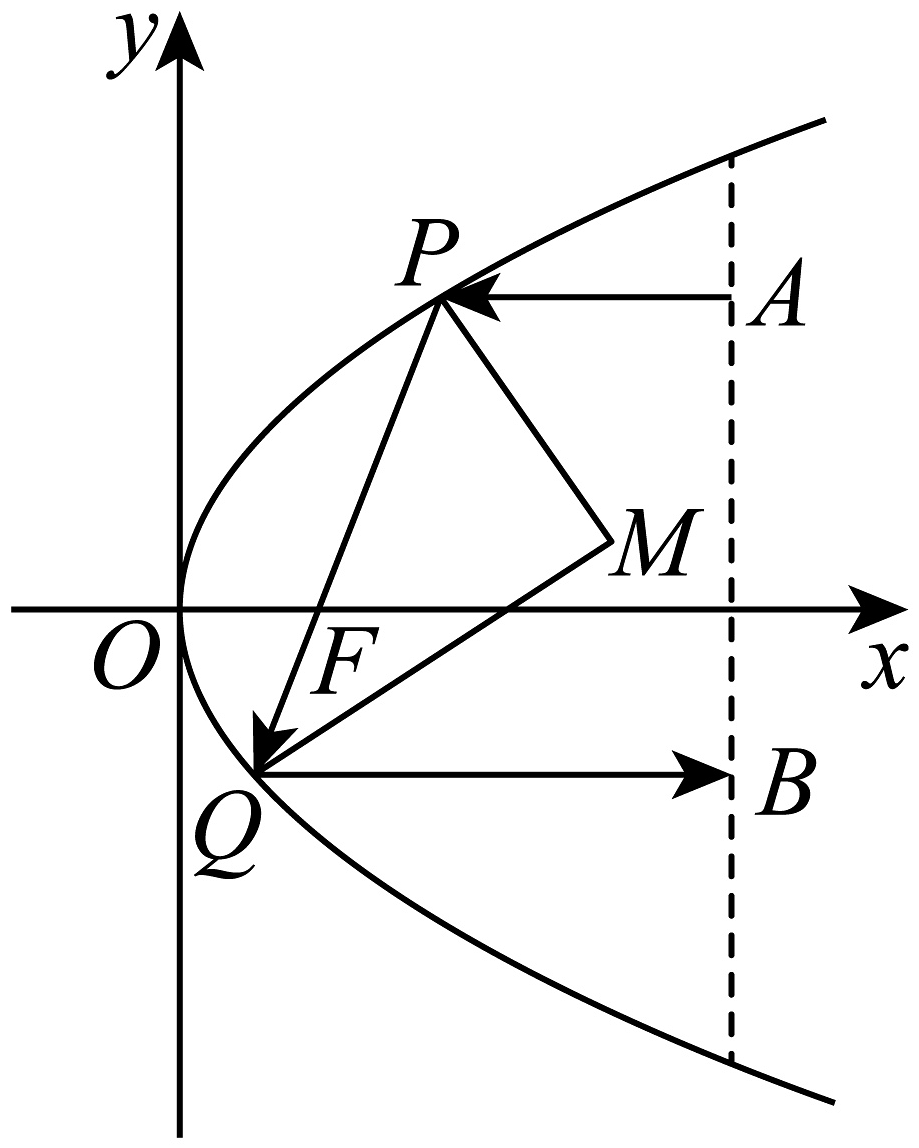 A、 B、若 , 则直线的斜率为 C、存在直线 , 使得 , , , 四点共圆 D、面积的最小值为1
A、 B、若 , 则直线的斜率为 C、存在直线 , 使得 , , , 四点共圆 D、面积的最小值为1三、填空题:本题共3小题,每小题5分,共15分.
-
12. 已知函数在上单调递增,函数是定义在上的奇函数,且 , 则可以是.(写出一个满足条件的函数即可)13. 已知 , 为椭圆的左、右焦点,点 , 在上,若等边三角形的重心为 , 则的离心率为.14. 两个不透明的袋子中均装有1个红球,2个白球,2个黑球(除颜色外,质地大小均相同),从两个袋子中同时取出1个球(取出的球不放回袋中),若两球颜色相同,则记1分,否则记0分,则取球5次后,总得分大于2的概率为.
四、解答题:本题共5小题,共77分.解答应写出必要的文字说明、证明过程及演算步骤.
-
15. 记的内角 , , 的对边分别为 , , , 且 .(1)、求;(2)、若 , 且边上的高为 , 求的周长.16. 已知函数 , .(1)、若 , 求图象在点处的切线方程;(2)、若函数在上的最小值是 , 求的值.17. 如图,在多面体中,是边长为2的等边三角形,平面 , , , , , 设为的中点.
 (1)、证明:平面;(2)、设为棱上的动点,求与平面所成角的正弦值的最大值.
(1)、证明:平面;(2)、设为棱上的动点,求与平面所成角的正弦值的最大值.