湖南省株洲市第十三中学2024—2025学年高一下学期期末摸底考试数学试题（A）

试卷更新日期：2025-07-01 类型：期末考试

进入出卷网下载

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求.

1. 复数 $\frac{5}{- 2 + i} =$ （）

A、 $2 + i$ B、 $- 2 + i$ C、 $- 2 - i$ D、 $2 - i$

查看试题解析
2. 已知向量 $\vec{a} = (x, - 1)$ ， $\vec{b} = (- 2, 3)$ ，若 $\vec{a} / / \vec{b}$ ，则 $x =$ （）

A、 $- \frac{2}{3}$ B、 $\frac{2}{3}$ C、 $- \frac{3}{2}$ D、 $\frac{3}{2}$

查看试题解析
3. 在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，P为棱 $A A_{1}$ 的中点，则点B到直线 $C_{1} P$ 的距离为（）

A、2 B、 $\sqrt{3}$ C、 $\sqrt{2}$ D、1

查看试题解析
4. 设 $m$ ， $n$ 是两条不同的直线， $α$ ， $β$ 是两个不同的平面，下列命题中错误的是（）

A、若 $m ⊥ α$ ， $m // n$ ， $n // β$ ，则 $α ⊥ β$ B、若 $α // β$ ， $m \subset α$ ，则 $m // β$ C、若 $m ⊥ n$ ， $m \subset α$ ， $n \subset β$ ，则 $α ⊥ β$ D、若 $m // n$ ， $α // β$ ，则 $m$ 与 $α$ 所成的角和 $n$ 与 $β$ 所成的角相等

查看试题解析
5. 一个正四棱台的上底面边长为1，下底面边长为2，若一个球与该正四棱台的各面均相切，则该球的体积为（）

A、 $\frac{\sqrt{2}}{6} π$ B、 $\frac{\sqrt{2}}{3} π$ C、 $\frac{2 \sqrt{2}}{3} π$ D、 $2 π$

查看试题解析
6. 若函数 $f (x) = A cos (ω x + φ)$ （ $A > 0$ ， $ω > 0$ ， $- π < φ < π$ ）的图象上有两个相邻顶点为 $M (- 3, \sqrt{3})$ ， $N (1, - \sqrt{3})$ .将 $f (x)$ 的图象沿x轴向左平移1个单位，再沿y轴向上平移 $\sqrt{3}$ 个单位后得 $g (x)$ ，则 $g (\frac{4}{3})$ 为（）

A、 $\sqrt{3}$ B、 $- \frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $2 \sqrt{3}$

查看试题解析
7. 在菱形 $A B C D$ 中， $∠ A = 60 °, A B = \sqrt{3}$ ，将 $△ A B D$ 折起到 $△ P B D$ 的位置，若三棱锥 $P - B C D$ 的外接球的体积为 $\frac{7 \sqrt{7} π}{6}$ ，则二面角 $P - B D - C$ 的正弦值为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{\sqrt{7}}{3}$

查看试题解析
8. 在 $△ A B C$ 中， $a b = 2, a^{2} + 3 c^{2} = b^{2}$ ，若以m为参数的不等式 $\cos 2 C + 2 m \sin (A + B) + m^{2} - 2 \geq 0$ 恒成立，则m的取值范围是（）

A、 $(- \infty, - 1] \cup [1, + \infty)$ B、 $(- \infty, - \frac{1 + 2 \sqrt{3}}{3}] \cup [1, + \infty)$ C、 $[- \frac{1 + 2 \sqrt{3}}{3}, - 1] \cup [\frac{2 \sqrt{3} - 1}{3}, 1]$ D、 $[- \frac{1 + 2 \sqrt{3}}{3}, \frac{2 \sqrt{3} - 1}{3}]$

查看试题解析

二、多项选择题：本题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分.

9. 下列说法正确的是（）

A、某人掷骰子1次，“掷出5”与“掷出6”是互斥事件 B、甲、乙、丙三种个体按 $1 : 2 : 3$ 的比例分层抽样，如果抽取的甲个体数为3，则抽取的丙个体数为9 C、数据 $4$ ， $3$ ， $4$ ， $6$ ， $8$ ， $7$ ， $8$ ， $9$ 的 $60 %$ 分位数是8 D、数据 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， …， $a_{n}$ 的方差为 $s^{2}$ ，则数据 $3 a_{1}$ ， $3 a_{2}$ ， $3 a_{3}$ ， …， $3 a_{n}$ 的方差为 $9 s^{2}$

查看试题解析
10. 已知 $f (x) = {log}_{2} (x^{2} - m x + m + 3)$ 的定义域为 $D$ ，值域为 $M$ ，则（）

A、若 $D = R$ ，则 $M \neq R$ B、对任意 $m \in R$ ，使得 $f (- 5) = f (- 7)$ C、对任意 $m \in R, f (x)$ 的图象恒过一定点 $(1, 2)$ D、若 $f (x)$ 在 $(- \infty, 3)$ 上单调递减，则 $m$ 的取值范围是 $\{6\}$

查看试题解析
11. 在△ABC中，角A，B，C的对边分别是a，b，c，且满足 $b \sin A = a \cos (B - \frac{π}{6})$ ，则（）

A、 $B = \frac{π}{6}$ B、若b＝4，则△ABC的周长的最大值为 $12$ C、若D为AC的中点，且BD＝2，则△ABC的面积的最大值为 $\frac{4 \sqrt{3}}{3}$ D、若角B的平分线BD与边AC相交于点D，且 $B D = \sqrt{3}$ ，则a+4c的最小值为9

查看试题解析

三、填空题：本题共3小题，每小题5分，共15分.

12. 计算 ${(\frac{3 + i}{2 - i})}^{2} =$ ．

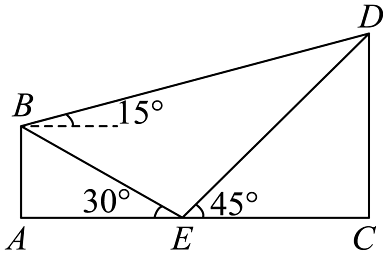
查看试题解析
13. 香霏楼是荣昌昌州故里景区的标志性建筑之一，也是荣昌历史文化的重要象征.某同学为测量香霏楼的高度 $C D$ ，在香霏楼的正西方向找到一座建筑物 $A B$ ，高约为15m，在地面上点E处（A，C，E三点共线）测得建筑物顶部B，香霏楼顶部D的仰角分别为 $30 °$ 和 $45 °$ ，在B处测得塔顶部D的仰角为 $15 °$ ，则香霏楼的顶部与地面的距离约为 m..

查看试题解析
14. 已知平面 $α / / β$ ，直线 $l$ 与 $α$ 所成角的正切值为 $\frac{\sqrt{2}}{2}$ ，直线 $m \subset α ， l ⊥ m$ ，直线 $n \subset β$ ，且 $l$ 和 $n$ 所成角为 $\frac{π}{4}$ ，那么 $m$ 与 $n$ 所成的角为.

查看试题解析

四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.

15. 已知平面向量 $\vec{a} = (1, x)$ ， $\vec{b} = (2 x + 3, - x)$ ．

(1)、若 $\vec{a} ⊥ \vec{b}$ ，求 $x$ 的值；

(2)、若 $\vec{a} / / \vec{b}$ ，求 $|\vec{a} - \vec{b}|$ ．

查看试题解析
16. 已知函数 $f (x) = (\cos \frac{x}{2} + \sin \frac{x}{2}) (\cos \frac{x}{2} - \sin \frac{x}{2}) + \sin x$ .

(1)、求函数 $f (x)$ 的最小正周期及单调递增区间；

(2)、将函数 $f (x)$ 的图象上所有点向上平移 $1$ 个单位得到曲线 $C_{1}$ ，再将 $C_{1}$ 上的各点纵坐标变为原来的 $2$ 倍（横坐标不变），得到函数 $g (x)$ 的图象．若 $\exists x \in [0, \frac{π}{2}]$ ， $\forall m \in [- 1,0]$ ，不等式 $m t^{2} - 2 m t + 7 \geq g (x)$ 成立，求实数 $t$ 的取值范围．

查看试题解析
17. 如图，在直角坐标系 $x O y$ 中，点P是单位圆上的动点，过点P作x轴的垂线，垂足为M，过O作射线交 $M P$ 的延长线于点Q，使得 $S_{△ O Q M} = 2 S_{△ O P M}$ ，记 $∠ M O P = α$ ， $∠ Q O M = β$ ，且 $α \in (0, \frac{π}{2})$ ．

(1)、若 $\sin α = \frac{3}{5}$ ，求 $\frac{\sin (- β) + \cos (π - β)}{cos (\frac{π}{2} - β) + sin (\frac{3 π}{2} + β)}$ 的值；

(2)、已知函数 $f (α) = 1 - 2 m - 2 m \sin α - 2 \cos^{2} α$ ， $α \in [\frac{π}{6}, \frac{π}{3}]$ ，记 $f (α)$ 的最小值为 $g (m)$ ．若 $g (m) = \frac{1}{2}$ ，求m的值及此时 $f (α)$ 的最大值．

查看试题解析
18. 如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，侧面 $A B B_{1} A_{1}$ 是正方形， $A B = B C = 2, ∠ A B C = 90 °$ ， $E, F$ 分别是棱 $A C, A B$ 的中点，且 $\vec{B_{1} D} = λ \vec{B_{1} A_{1}} (0 \leq λ \leq 1)$ ．

(1)、若 $λ = \frac{1}{2}$ ，证明： $D E / /$ 平面 $C B B_{1} C_{1}$ ；

(2)、当平面 $D E F$ 与平面 $A_{1} B C$ 夹角的余弦值最大时，求 $λ$ 的值．

查看试题解析
19. 设定义域为 $R$ 的函数 $y = f (x)$ 在 $R$ 上可导，导函数为 $y = f^{'} (x)$ ．若区间 $I$ 及实数 $t$ 满足： $f (x + t) \geq t \cdot f^{'} (x)$ 对任意 $x \in I$ 成立，则称函数 $y = f (x)$ 为 $I$ 上的“ $M (t)$ 函数”．

(1)、判断 $y = x^{2} + 3 x$ 是否为 $(0, + \infty)$ 上的 $M (1)$ 函数，说明理由；

(2)、若实数 $t$ 满足： $y = \sin x$ 为 $[0, \frac{π}{2}]$ 上的 $M (t)$ 函数，求t的取值范围；

(3)、已知函数 $y = f (x)$ 存在最大值．求证：对任意正整数 $n, y = f (x)$ 都是 $R$ 上 $M (n)$ 的函数的充要条件是对任意 $x \in R, f^{'} (x) \leq 0$ 与 $f (x) \geq 0$ 恒成立

查看试题解析