广东省深圳中学初中部 2024-2025学年下学期八年级数学期末试题

试卷更新日期：2025-07-18 类型：期末考试

进入出卷网下载

一、单选题(共8小题，每小题3分，共24分.在每小题给出的选项中，只有一项是符合题目要求的.)

1. 下列性质中菱形一定具有的是( )

A、对角线相等 B、有一个角是直角 C、对角线互相垂直 D、四个角相等

查看试题解析
2. 用配方法解一元二次方程 $x^{2} - 4 x - 3 = 0,$ 下列配方正确的是( )

A、 ${(x + 2)}^{2} = 2$ B、 ${(x - 2)}^{2} = 7$ C、 ${(x + 2)}^{2} = 7$ D、 ${(x - 2)}^{2} = 1$

查看试题解析
3. 如图，在四边形ABCD中，AB∥CD，添加下列一个条件后，能判定四边形ABCD是平行四边形的是( )

A、AD=BC B、AD∥BC C、AB=BC D、∠B=2∠A

查看试题解析
4. 如图， BE是平行四边形ABCD的外角平分线， ∠A+∠C=220°，则∠CBE的度数是( )

A、50° B、55° C、52.5° D、57.5°

查看试题解析
5. 反比例函数 $y = \frac{- 2}{x},$ 下列说法不正确的是( )

A、图象经过点(1，-2) B、图象位于第二、四象限 C、图象关于直线y=x对称 D、y随x的增大而增大

查看试题解析
6. 如图，在平行四边形ABCD中，点P是BC边上的动点，连接AP， DP， E是AD的中点，F是PD的中点，点P从B点向C点的运动的过程中，EF的长度( )

A、保持不变 B、逐渐增大 C、先增大再减小 D、先减小再增大

查看试题解析
7. 如图，正方形ABCD的边长为2，E为BC边上的一点，以AE为边作矩形AEFG，使GF经过点D，则矩形AEFG的面积为( )

A、4 B、5 C、6 D、7

查看试题解析
8. 已知x₁ ， x₂是关于x的方程 $x^{2} - 2 (m + 1) x + m^{2} + 5 = 0$ 的两个实数根，已知等腰△ABC的一边长为3，若x₁ ， x₂恰好是△ABC另外两边长，则△ABC周长为( )

A、9 B、9或11 C、13 D、9或13

查看试题解析

二、填空题(共5小题，每小题3分，共15分.)

9. 方程 $x^{2} - 3 x - 5 = 0$ 的两根为 $x_{1}$ ， $x_{2}$ ，则 $x_{1} + x_{2}$ 的值为．

查看试题解析
10. 一个正多边形的每个外角都等于36°，那么它是边形.

查看试题解析
11. 如图，在平面直角坐标系中，点A在函数 $y = \frac{k}{x} (k > 0, x > 0)$ 的图象上，过点A作AB⊥x轴，取AB中点C，点D在y轴上，连接AD、CD， △ACD的面积为2，则k的值是.

查看试题解析
12. 如图，菱形ABCD中， $A B = 10, A C = 16,$ AC交BD于点O， $D E ⟂ B C$ 于点E，连接OE，则OE的长为.

查看试题解析
13. 如图，在等腰△ABC中， $A B = A C = 5, B C = 6,$ 将 $△ A B C$ 沿直线BC平移至 $△ A^{^{'}} B^{^{'}} C^{^{'}},$ 将点B绕点A逆时针旋转 $9 0^{\circ}$ 得到点D，连接DA'、DC'，在平移过程中， $∣ A^{'} D - C^{'} D ∣$ |的最大值为.

查看试题解析

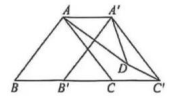
三、解答题(本题共7小题，其中第14题6分，第15题8分，第16题8分，第17题10分, 第18题8分, 第19题9分, 第20题12分, 共61分)

14. 解下列方程

(1)、 $2 x^{2} - 4 x - 1 = 0$

(2)、 $(2 - 3 x) + {(3 x - 2)}^{2} = 0$

查看试题解析
15. 如图，在正方形网格中，每个小正方形的边长均为1.每个小正方形的顶点叫做格点，以格点为顶点按下列要求画图.

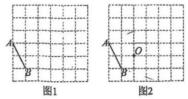(1)、在图1中画一个▱ABCD，使 $B C = 2 A B;$

(2)、在图2中画一个以点O为对称中心，A，B为顶点的 $▱ A B C D;$

(3)、图2中▱ABCD的面积为.

查看试题解析
16. 如图，一次函数 $y_{1} = k_{1} x + b$ 与反比例函数 $y_{2} = \frac{k_{2}}{x}$ 的图象交于点 $A (3, \frac{m}{3})$ 和 $B (- 2, m - 18) .$

(1)、根据函数图象可知，当 $y_{1} \leq y_{2}$ 时，x的取值范围是；

(2)、求反比例函数和一次函数的解析式.

查看试题解析
17. 如图，在平行四边形ABCD中，过点D作 $D E ⟂ A B$ 于点E，点F在边CD上， $C F = A E .$ 连接AF， BF.

(1)、求证：四边形BFDE是矩形；

(2)、若∠DAB=60°， AF平分. $∠ D A B, A D = 4,$ 求AB的长.

查看试题解析
18. 已知关于x的方程 $m x^{2} - 4 x + 4 - m = 0$

(1)、)求证：此方程总有实数根；

(2)、若m为整数，且此方程有两个互不相等的非负整数根，求m的值.

查看试题解析

19. 根据以下素材，探索完成任务.

背景	今年的春节动画电影“哪吒2”火爆影院，吸引了大量市民观影，各大影院积极推送.
素材1	某影院正月初一的票房收入费用为6万元，随着观影人数的不断增多，正月初三的票房收入达到8.64万元.
素材2	随着电影的爆火，某商家生产了一批“哪吒”手办盲盒进行销售.盲盒是一个长方体盒子，其底面面积是0.016m².如图，该长方体盒子可用矩形硬纸板的四个角分别剪去2个同样大小的长方形和2个同样大小的正方形，然后折叠成一个有盖的盒子制成.已知矩形硬纸板的长宽分别为26cm， 22cm.
素材3	已知一个“哪吒”手办的生产成本为30元，经销一段时间后发现：当该款手办售价定为65元/个时，平均每天售出30个；售价每降低1元，平均每天多售出3个，该店计划下调售价使平均每天的销售利润为1500元.
问题解决
⑴任务1	求从正月初一到正月初三该影院票房收入的天平均增长率.
⑵任务2	根据素材2，求矩形硬纸板剪去的正方形的边长.
⑶任务3	根据素材3，为了推广该款“哪吒”手办，且尽可能减少库存，求下调后每个手办的售价.

查看试题解析

20. 四边形ABCD是一张正方形纸片，小明用该纸片玩折纸游戏.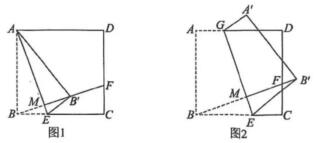

(1)、【探究发现】
如图1，小明将△ABE沿AE翻折得到 $△ A B' E,$ 点B 的对应点B'，将纸片展平后，连接BB'并延长交边CD于点F，小明发现折痕AE与BF存在特殊的数量关系，数量关系为；

(2)、【类比探究】
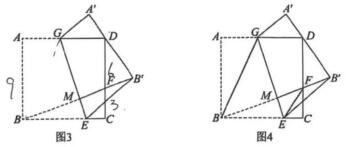
如图2，小明继续折纸，将四边形ABEG沿GE所在直线翻折得到四边形A'B'EG，点A 的对应点为点A'，点B 的对应点为点 B'，将纸片展平后，连接BB'交边CD于点F，请你猜想线段AG，CE，DF之间的数量关系并证明：

(3)、【拓展延伸】
在(2) 的翻折过程中，正方形ABCD的边长为9， CF=3.
①如图3，若线段 $A^{'} B^{'}$ 恰好经过点D，求AG的长，
②如图4，连接BG， EF，直接写出 $B G + E F$ 的最小值.

查看试题解析