广东省深圳外国语学校2024-2025学年七年级下学期期末数学试题
试卷更新日期:2025-07-18 类型:期末考试
一、单选题
-
1. 以下是四款常用的人工智能大模型的图标,其文字上方的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、 B、 C、 D、3. 如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为 , , .让转盘自由转动,转盘停止后指针(指针指向分隔线,则重新转动转盘)落在红色区域的概率是( )
2. 下列运算正确的是( )A、 B、 C、 D、3. 如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为 , , .让转盘自由转动,转盘停止后指针(指针指向分隔线,则重新转动转盘)落在红色区域的概率是( )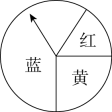 A、 B、 C、 D、4. 图1 为我国高铁座位的实物图,图2 是它的简易图,座位和座椅靠背的夹角 , 小桌板与座位平行,小桌板支撑杆与桌面的夹角 , 则座椅靠背与小桌板支撑杆形成的夹角的度数是( )
A、 B、 C、 D、4. 图1 为我国高铁座位的实物图,图2 是它的简易图,座位和座椅靠背的夹角 , 小桌板与座位平行,小桌板支撑杆与桌面的夹角 , 则座椅靠背与小桌板支撑杆形成的夹角的度数是( )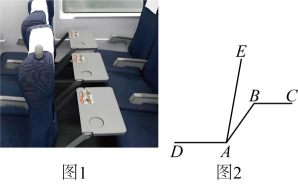 A、 B、 C、 D、5. 下列说法不正确的是( )A、锐角三角形中每个内角都小于是必然事件 B、翻开数学课本,恰好翻到30页是随机事件 C、竹篮打水属于不可能事件 D、在纸上任意画两条直线,这两条直线互相平行是必然事件6. 如图,两个边长相等的正方形和 , 将正方形的顶点E与正方形的中心重合,正方形绕点E 顺时针方向旋转;设旋转的角度为 , 两个正方形重叠部分的面积为S,则变量S与θ的关系大致图象是( )
A、 B、 C、 D、5. 下列说法不正确的是( )A、锐角三角形中每个内角都小于是必然事件 B、翻开数学课本,恰好翻到30页是随机事件 C、竹篮打水属于不可能事件 D、在纸上任意画两条直线,这两条直线互相平行是必然事件6. 如图,两个边长相等的正方形和 , 将正方形的顶点E与正方形的中心重合,正方形绕点E 顺时针方向旋转;设旋转的角度为 , 两个正方形重叠部分的面积为S,则变量S与θ的关系大致图象是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 如图,和是分别沿着边翻折形成的,与交于点O,若 , 则的度数为( )
7. 如图,和是分别沿着边翻折形成的,与交于点O,若 , 则的度数为( )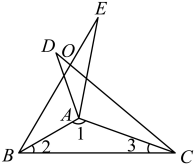 A、 B、 C、 D、8. 如图在四边形中 , , , 面积为 24,的垂直平分线分别交 , 于点M,N,若点P和点Q分别是线段和边上的动点,则的最小值为( )
A、 B、 C、 D、8. 如图在四边形中 , , , 面积为 24,的垂直平分线分别交 , 于点M,N,若点P和点Q分别是线段和边上的动点,则的最小值为( )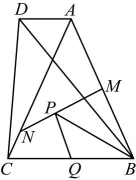 A、6 B、7 C、8 D、9
A、6 B、7 C、8 D、9二、填空题
-
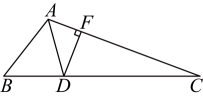
9. 在一个不透明的盒子中装有4个白球,n个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是白球的概率为 , 则 .10. 某商场自行车存放处每周存车量5000辆次,其中变速车车费是每辆一次1元,普通车存车费每辆一次0.5元,若普通车存车量为辆次,存车的总收入为元,则和之间的关系式为.11. 若 , , 则 .12. 如图,在中,平分 , 垂足为 , 则的长为 .
 13. 如图,在中, , 分别以、、为边向上作正方形、正方形、正方形 , 点E在上,若 , , 则图中阴影的面积为 .
13. 如图,在中, , 分别以、、为边向上作正方形、正方形、正方形 , 点E在上,若 , , 则图中阴影的面积为 .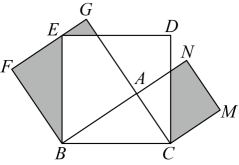
三、解答题
-
14. 计算:(1)、;(2)、 .15. 先化简, 再求值∶ , 其中 .16. 背景资料:“低碳生活”是指人们生活中尽量减少所耗能量,从而降低(特别是二氧化碳的)排放量的一种生活方式.低碳生活的理念也已逐步被人们所接受.相关资料统计了一系列排碳计算公式,根据信息,解决问题:
排碳计算公式
家居用电的二氧化碳排放量耗电量
开私家车的二氧化碳排放量耗油量
家用天然气的二氧化碳排放量天然气使用量
家用自来水的二氧化碳排放量自来水使用量
(1)、若x表示耗油量,开私家车的二氧化碳排放量为y,则开私家车的二氧化碳排放量与耗油量的关系式为 .(2)、在上述关系中,耗油量每增加 , 二氧化碳排放量就增加;当耗油量从增加到时,二氧化碳排放量就从 增加到 .(3)、小明家本月家居用电约 , 天然气 , 自来水 , 开私家车耗油 , 请你计算一下小明家这几项二氧化碳排放量的总和.17. 尺规作图题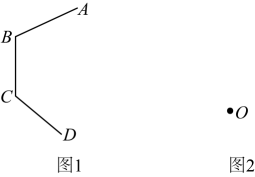 (1)、图1,校园一角的形状如图所示,其中 , , 表示围墙,小亮通过作角平分线在图示的区域中找到了一点P,使得点P到三面墙的距离都相等,请你用尺规作图法帮小亮画出P点.(保留作图痕迹,作图痕迹要清晰)(2)、图2,已知一个点O,请用尺规作图作一个以点O为顶点的直角 . (保留作图痕迹,作图痕迹要清晰)18. 如图, 在中, , 点D、E是边上两点,连接 , 以为腰作等腰直角 , , 作于点E, , 作于点G.
(1)、图1,校园一角的形状如图所示,其中 , , 表示围墙,小亮通过作角平分线在图示的区域中找到了一点P,使得点P到三面墙的距离都相等,请你用尺规作图法帮小亮画出P点.(保留作图痕迹,作图痕迹要清晰)(2)、图2,已知一个点O,请用尺规作图作一个以点O为顶点的直角 . (保留作图痕迹,作图痕迹要清晰)18. 如图, 在中, , 点D、E是边上两点,连接 , 以为腰作等腰直角 , , 作于点E, , 作于点G.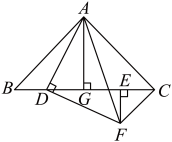 (1)、证明∶;(2)、若 , , 求的大小.19. 数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b、宽为a的长方形,并用A种纸片一张, B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)、证明∶;(2)、若 , , 求的大小.19. 数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b、宽为a的长方形,并用A种纸片一张, B种纸片一张,C种纸片两张拼成如图2的大正方形.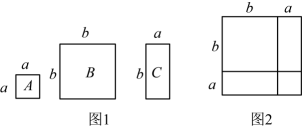 (1)、若要拼出一个面积为的长方形,则需要A号卡片1张,B号卡片2张,C号卡片张.(2)、根据所学知识,解决如下问题:
(1)、若要拼出一个面积为的长方形,则需要A号卡片1张,B号卡片2张,C号卡片张.(2)、根据所学知识,解决如下问题:已知: , , 的值为;
小明在数学课外书上看到了这样一道题:如果x满足 . 求 的值,怎么解决呢?
小英给出了如下两种方法:
方法1∶ 设 , 则;
,
,
,
,
,
;
方法2:
∵ ,
,
,
.
(3)、任务:请你用材料中两种方法中的一种解答问题:若 , 求 的值.
(4)、如图,在长方形中, , , E , F分别是上的点,且 , 分别以为边在长方形外侧作正方形和若长方形的面积为 40,则图中阴影部分的面积和为 .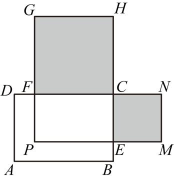 20.
20.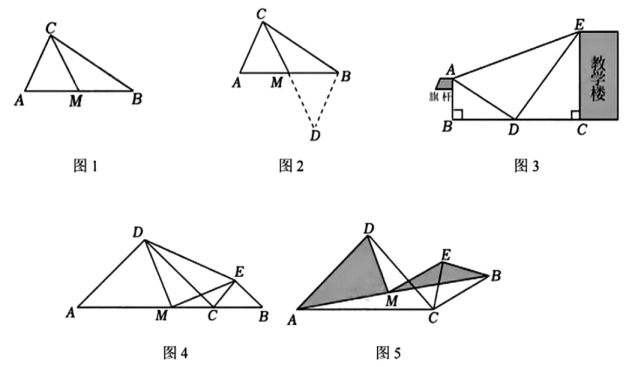 (1)、【阅读理解】中线是三角形中的重要线段之一.在利用中线解决几何问题时,当条件中出现“中点”、“中线”等条件时,可以考虑作辅助线,即把中线延长一倍,通过构造全等三角形,把分散的已知条件和所要求的结论集中到同一个三角形中,从而运用全等三角形的有关知识来解决问题,这种作辅助线的方法称为“倍长中线法”.如图1,在中,CM为的中线,若 , 求的取值范围.
(1)、【阅读理解】中线是三角形中的重要线段之一.在利用中线解决几何问题时,当条件中出现“中点”、“中线”等条件时,可以考虑作辅助线,即把中线延长一倍,通过构造全等三角形,把分散的已知条件和所要求的结论集中到同一个三角形中,从而运用全等三角形的有关知识来解决问题,这种作辅助线的方法称为“倍长中线法”.如图1,在中,CM为的中线,若 , 求的取值范围.倍长中线法:如图2,延长至点D,使得 , 连结 , 可证明 , 由全等得到 , 从而在中,根据三角形三边关系可以确定的范围,进一步即可求得的范围为;
(2)、【实践应用】为了测量学校旗杆和教学楼顶端之间的距离,学习小组设计了如图3所示的测量方案,他们首先取地面的中点D,用测角仪测得此时测得旗杆高度 , 教学楼高度 , 则的长为m;(3)、【拓展探究】如图4,C为线段上一点, , 分别以为斜边向上作等腰和等腰 , M为中点, 连结 .① 判断的形状,并证明;
② 若将图4中的等腰绕点C转至图5的位置(A,C,B不在同一条直线上),连结 , M为中点,且D,E在同侧,连结 . 若 , , 则与的面积之差为 ▲ .