湖南省名校联考联合体2025届高考考前仿真联考(三)数学试题

试卷更新日期：2025-06-01 类型：高考模拟

进入出卷网下载

一、选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 已知集合 $A = \{- 4, - 3, - 2, - 1, 0, 1\}$ ， B= $\{x | - 4 ＜ x ＜ 1\}$ ，则 $A \cap B =$ （）

A、 $\{- 4, - 3, - 2, - 1, 0, 1\}$ B、 $\{x | - 4 ＜ x ＜ 1\}$ C、 $\{- 3, - 2, - 1, 0\}$ D、 $\emptyset$

查看试题解析
2. 若 $1 - b i = (1 - i) (2 + a i)$ （a， $b \in R$ ， i为虚数单位），则 $a + b$ 的值为（）

A、2 B、1 C、 $- 2$ D、 $- 3$

查看试题解析
3. 已知 $\sin (\frac{π}{4} - θ) = \frac{\sqrt{3}}{3}$ ，则 $\sin 2 θ =$ （）

A、 $- \frac{2}{3}$ B、 $- \frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{3}$

查看试题解析
4. 在 $△ A B C$ 中，点 $D$ 是线段 $B C$ 上一点，若 $\vec{B D} = λ \vec{B C}$ ， $\vec{A D} = \frac{1}{4} \vec{A B} + \frac{3}{4} \vec{A C}$ ，则实数 $λ =$ （）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
5. 已知曲线 $C : \frac{x^{2}}{6 - t} + \frac{y^{2}}{t - 2} = 1$ ，设 $p : 2 < t < 3$ ， q：曲线C是焦点在x轴上的椭圆，则p是q的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
6. 在 $△ A B C$ 中，角A，B，C的对边分别是a，b，c，已知 $A = \frac{π}{4}$ ， $b = 3$ ，三角形ABC的面积为6，则 $a =$ （）

A、65 B、17 C、 $\sqrt{17}$ D、 $\sqrt{65}$

查看试题解析
7. $(\frac{1}{x^{2}} - 2) {(1 + x)}^{5}$ 的展开式中的常数项是（）

A、12 B、8 C、 $- 8$ D、 $- 12$

查看试题解析
8. 若直线 $y = k x + 1$ （k为常数）是曲线 $y = \ln x + 1$ 和曲线 $y = a e^{x} + 1$ 的公切线，则实数a的值为（）

A、 $\frac{1}{e}$ B、 $\frac{1}{e^{2}}$ C、1 D、e

查看试题解析

二、选择题（本大题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．）

9. 已知函数 $f (x) = 2 \sin (2 x + \frac{π}{6})$ ，则下列结论正确的是（）

A、函数 $f (x)$ 的图象关于直线 $x = \frac{π}{6}$ 对称 B、函数 $f (x)$ 的振幅为 $\pm 2$ C、函数 $f (x)$ 在区间 $(- \frac{π}{3}, 0)$ 上单调递增 D、若函数 $g (x) = f (x) - a$ 在区间 $[0, \frac{π}{2}]$ 上恰有两个不同零点，则实数a的取值范围为 $[1, 2)$

查看试题解析
10. 已知动点P到定点 $F (0, 1)$ 的距离与到定直线 $l : y = 3$ 的距离之和为4，记动点P的轨迹为曲线C，则下列结论正确的是（）

A、曲线C的轨迹方程为 $x^{2} + {(y - 1)}^{2} = {(4 - |y - 3|)}^{2}$ B、曲线C的图象关于y轴对称 C、若点 $(x_{0}, y_{0})$ 在曲线C上，则 $- 2 \sqrt{3} < x_{0} < 2 \sqrt{3}$ D、曲线C上的点到直线 $\sqrt{3} x - y - 15 = 0$ 的距离的最大值为12

查看试题解析
11. 已知定义在R上的函数 $f (x)$ 满足：对任意实数x，y，恒有 $[f (x) + 1] \cdot [f (y) + 1] = f (x + y) + 1$ ，若 $f (1) = 1$ ，当 $x < 0$ 时， $f (x) < 0$ ，则下列结论正确的是（）

A、 $f (0) = 0$ B、函数 $f (x)$ 的最小值为 $- 1$ C、 $f (x)$ 为R上的增函数 D、关于x的不等式 $f (x) + f (2 - x) > 3$ 的解集为 $(- \infty, 0) \cup (2, + \infty)$

查看试题解析

三、填空题（本大题共3小题，每小题5分，共15分．）

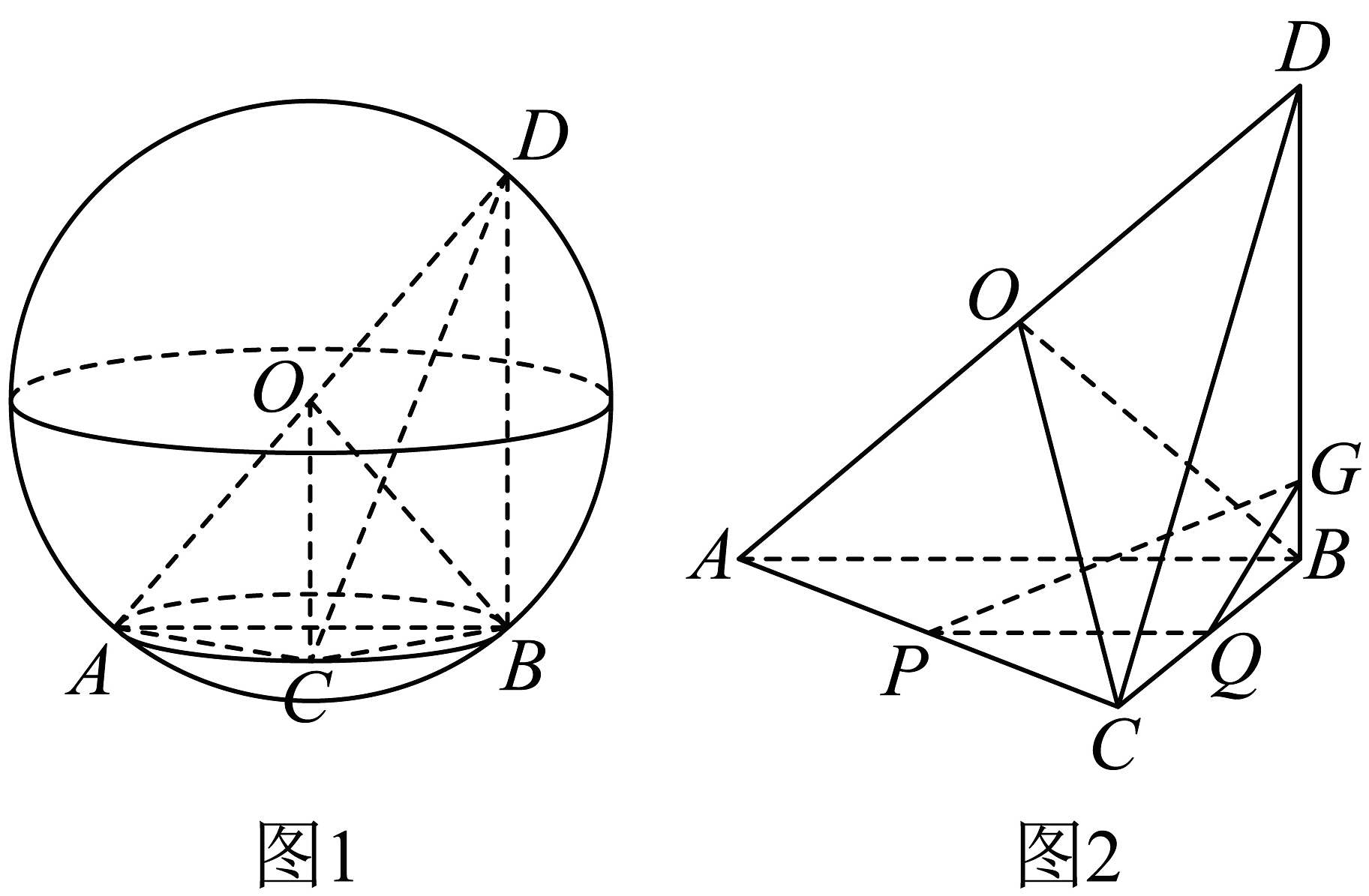
12. 甲、乙两人向同一目标各射击1次，已知甲、乙命中目标的概率分别为 $\frac{3}{4}$ ， $\frac{4}{5}$ ，则目标至少被击中1次的概率为．

查看试题解析
13. 已知函数 $f (x)$ 的定义域为R ，且 $f (x + 2) = f (x)$ ，当 $x \in [0, 1)$ 时， $f (x) = 2^{x} - 1$ ，则 $f (\log_{2} \frac{1}{3})$ 的值为．

查看试题解析
14. 如图1，已知球O的半径 $R = \sqrt{3}$ ．在球O的内接三棱锥 $D - A B C$ 中． $D B ⊥$ 平面 $A B C$ ， $A C ⊥ B C$ ， $A C = \sqrt{2} B C$ ， $B D = \sqrt{6}$ ． P，Q分别为线段AC，BC的中点，G为线段BD上一点（不与点B重合），如图2．则平面 $O B C$ 与平面 $G P Q$ 夹角的余弦值的最大值为．

查看试题解析

四、解答题（本大题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．）

15. 中国的非遗项目丰富多样，涵盖广泛，体现了中华民族的智慧和独特的文化魅力．春节期间某地为充分宣扬该地非遗物质文化，加大非遗传承人的技艺展示．该地市场开发与发展机构统计了非遗传承人的技艺展示量与市场消费收入的6组数据如下表：
技艺展示量x（单位：个）
21
23
24
27
29
32
市场消费收入y（单位：万元）
6
11
20
27
57
77

(1)、若用线性回归理论进行统计分析，求市场消费收入y关于技艺展示量x的回归方程 $\hat{y} = \hat{b} x + \hat{a}$ （精确到0.1）；

(2)、若用非线性回归模型求得市场消费收入y关于技艺展示量x的回归方程为 $\hat{y} = 0.06 e^{0.2303 x}$ ，且决定系数 $R^{2} = 0.9522$ ，与（1）中的线性回归模型相比，应用决定系数 $R^{2}$ 说明哪种模型的拟合效果更好．
附：一组数据 $(x_{1}, y_{1})$ ， $(x_{2}, y_{2})$ ， …， $(x_{n}, y_{n})$ ，其回归直线 $\hat{y} = \hat{b} x + \hat{a}$ 的斜率和截距的最小二乘估计为 $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i}, \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ；决定系数 $R^{2} = 1 - \frac{\sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}$
参考数据： $\sum_{i = 1}^{6} (x_{i} - \bar{x}) (y_{i} - \bar{y}) = 557$ ， $\sum_{i = 1}^{6} {(x_{i} - \bar{x})}^{2} = 84$ ， $\sum_{i = 1}^{6} {(y_{i} - \bar{y})}^{2} = 3930$ ，
线性回归模型的残差平方和为 $\sum_{i = 1}^{6} {(y_{i} - {\hat{y}}_{i})}^{2} = 236 .64$ （其中 $x_{i}$ ， $y_{i}$ 分别为非遗传承人的技艺展示量和市场消费收入， $i = 1, 2, 3, 4, 5, 6$ ）．

查看试题解析
16. 如图，在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A A_{1} = 2 A B = 2 A D$ ，点E是棱 $C C_{1}$ 的中点．

(1)、求证： $A C_{1} //$ 平面BDE；

(2)、求直线 $B C_{1}$ 与平面BDE所成角的正弦值．

查看试题解析
17. 已知函数 $f (x) = x (2 \ln x + a)$ ， $a \in R$ ．

(1)、若函数 $f (x)$ 在 $(e^{2}, + \infty)$ 上单调递增，求实数a的取值范围；

(2)、若 $x = e$ 为函数 $f (x)$ 的极值点，求a的值；

(3)、设函数 $g (x) = 4 x^{2} - 4 b x$ ，当 $a = - 2$ 时，若对于任意 $x_{1} \in (0, + \infty)$ ，总存在 $x_{2} \in [- 2, 4]$ ，使得 $g (x_{2}) \leq f (x_{1})$ ，求实数b的取值范围．

查看试题解析
18. 已知非零等差数列 $\{a_{n}\}$ 的前n项和为 $S_{n}$ ，且 $a_{2} = 4$ ， $a_{n} \cdot a_{n + 1} = 4 S_{n}$ ．

(1)、求 $\{a_{n}\}$ 的通项公式；

(2)、已知正项数列 $\{b_{n}\}$ 满足： $b_{1} = \frac{1}{3}$ ，且 $b_{n + 1}$ 是 $b_{n}$ 和 $b_{n} b_{n + 1}$ 的等差中项，求数列 $\{(\frac{1}{b_{n}} - 1) \cdot a_{n}\}$ 的前n项和 $T_{n}$ ；

(3)、在条件（2）下，记正项数列 $\{b_{n}\}$ 的前n项和为 $M_{n}$ ．求证： $\frac{2}{3} [1 - {(\frac{1}{2})}^{n}] \leq M_{n} < \frac{5}{6}$ ．

查看试题解析
19. 已知双曲线 $Γ : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 的左、右顶点分别是 $A_{1}$ ， $A_{2}$ ，点 $E (\sqrt{3}, 1)$ 在双曲线 $Γ$ 上，且直线 $A_{1} E$ ， $A_{2} E$ 的斜率之积为1．

(1)、求双曲线 $Γ$ 的标准方程；

(2)、已知 $F_{1}$ ， $F_{2}$ 分别是双曲线 $Γ$ 的左、右焦点，点G是圆 ${(x - 2)}^{2} + {(y - 3)}^{2} = \frac{1}{2}$ 上的动点，若K是双曲线 $Γ$ 左支上一动点，求 $|K F_{2}| + |K G|$ 的最小值；

(3)、已知两平行直线 $l_{1}$ 和 $l_{2}$ ，直线 $l_{1}$ 过点 $(2, 0)$ 交双曲线 $Γ$ 的右支于A，B两点，直线 $l_{2}$ 过点 $(8, 0)$ 交双曲线 $Γ$ 的右支于C，D两点，记AB，CD的中点分别为P，Q，过点Q作双曲线 $Γ$ 的两条渐近线的垂线，垂足分别为M，N．求四边形PMQN面积的取值范围．

查看试题解析

技艺展示量x（单位：个）	21	23	24	27	29	32
市场消费收入y（单位：万元）	6	11	20	27	57	77