江苏省南师附中、天一中学、海门中学、海安中学2024-2025学年高二下学期6月联考数学试题

试卷更新日期：2025-06-25 类型：期末考试

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 已知集合 $M = {x ∣ 0 < x < a}, N = \{x ∣ x^{2} - 6 x + 5 < 0\}$ ，若 $N \cup M = M$ ，则实数 $a$ 的取值范围是（）

A、 $[5, + \infty)$ B、 $(5, + \infty)$ C、 $[3 ， + \infty)$ D、 $(3, + \infty)$

查看试题解析
2. 已知直线 $a ∥$ 平面 $α$ ，则“直线 $b ⊥$ 平面 $α$ ”是“ $a ⊥ b$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
3. 已知函数 $f (x)$ 在 $R$ 上可导，且满足 $\lim_{Δ x \to 0} \frac{f (2) - f (2 + Δ x)}{2 Δ x} = 1$ ，则函数 $f (x)$ 在点 $(2, f (2))$ 处切线的斜率为（）

A、 $- 2$ B、2 C、 $- 1$ D、1

查看试题解析
4. 若5名学生报名参加数学、计算机、航模兴趣小组，每人选报1项，则不同的报名方式有（）

A、 $5^{3}$ 种 B、 $3^{5}$ 种 C、 $A_{5}^{3}$ 种 D、 $C_{5}^{3}$ 种

查看试题解析
5. 在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $B C_{1}$ 与 $B_{1} C$ 相交于点 $O$ ， $∠ B A C = 90^{°}$ ， $∠ A_{1} A B = ∠ A_{1} A C = 60 °$ ， $A_{1} A = 2$ ， $A B = A C = 1$ ，则线段 $A O$ 的长度为（）

A、 $\sqrt{2}$ B、 $\sqrt{10}$ C、 $\frac{\sqrt{10}}{2}$ D、 $2 \sqrt{2}$

查看试题解析
6. 已知奇函数 $f (x)$ 在 $x > 0$ 上满足 $f (x) = \frac{3}{4} f^{'} (1) \ln x + \frac{1}{2} x^{2} - 2 x$ ，其中 $f (x)$ 的导函数为 $f^{'} (x)$ ，则 $f (x)$ 的极大值点为（）

A、3 B、 $- 3$ C、1 D、 $- 1$

查看试题解析
7. 已知 $f (x) = \{\begin{matrix} (a - 2) x - a + 1, x < 1 \\ - a x^{2} + \ln x, x \geq 1 \end{matrix}$ 在 $(- \infty, + \infty)$ 上对任意 $x_{1}, x_{2}$ $(x_{1} \neq x_{2})$ 满足 $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} < 0$ ，则实数 $a$ 的取值范围为（）

A、 $[\frac{1}{2}, 2)$ B、 $(\frac{1}{2}, 2)$ C、 $(1, 2)$ D、 $[1, 2)$

查看试题解析
8. 甲袋中有3个白球和2个红球，乙袋中有2个白球和3个红球，先随机取一只袋，再从该袋中先后随机取2个球，则第一次取出的球是红球的条件下，第二次取出的球是白球的概率为（）

A、 $\frac{3}{10}$ B、 $\frac{1}{2}$ C、 $\frac{3}{5}$ D、 $\frac{5}{8}$

查看试题解析

二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．

9. 下列命题正确的是（）

A、两个随机变量的线性相关性越强，则样本相关系数越接近于1 B、对具有线性相关关系的变量 $x$ ， $y$ ，有一组观测数据 $(x_{i}, y_{i}) (i = 1, 2, \dots, 10)$ ，其经验回归方程是 $\hat{y} = \hat{b} x + 3$ ，且 $x_{1} + x_{2} + x_{3} + \dots + x_{10} = 3 (y_{1} + y_{2} + y_{3} + \dots + y_{10}) = 9$ ，则实数 $\hat{b}$ 的值是 $- 3$ C、已知随机变量 $X$ 的方差为4，则 $3 X + 2$ 的标准差是6 D、已知随机变量 $X ~ N (1, σ^{2})$ ，若 $P (X < - 1) = 0.3$ ，则 $P (X < 2) = 0.7$

查看试题解析
10. 已知 $(2 - x) {(1 + x)}^{2025} = a_{0} + a_{1} x + a_{2} x^{2} + \dots + a_{2026} x^{2026}$ ，则（）

A、 $a_{1} = 4049$ B、 $a_{0} + a_{2} + a_{4} + \dots + a_{2026} = 2^{2025}$ C、 $2^{2026} a_{0} + 2^{2025} a_{1} + 2^{2024} a_{2} + \dots + a_{2026} = 3^{2026}$ D、 $a_{1} + 2 a_{2} + 3 a_{3} + \dots + 2026 a_{2026} = 2024 \times 2^{2024}$

查看试题解析
11. 设事件 $A$ ， $B$ 满足 $0 < P (A) < P (A | \bar{B})$ ，则（）

A、 $A$ 与 $B$ 可能独立 B、 $A$ 与 $B$ 可能互斥 C、 $P (A) > P (A | B)$ D、 $P (B) < P (B | \bar{A})$

查看试题解析

三、填空题：本题共3小题，每小题5分，共15分．

12. 已知 $f (x) = \sin^{3} x + a x - 6$ ，且 $f (- 1) = 8$ ，则 $f (1) =$ ．

查看试题解析
13. ${(x + \frac{1}{x} + 2)}^{4}$ 的展开式的常数项是．

查看试题解析
14. 已知 $M = {x | 1 \leq x \leq 16, x \in N}$ ， $A = \{x_{1}, x_{2}, x_{3}\} \subseteq M$ ，且 $\frac{x_{1} + 2 x_{2} + 3 x_{3}}{3} \in Z$ ．则满足条件的集合 $A$ 共有个．

查看试题解析

四、解答题：本题共5小题，共77分．解答时应写出文字说明、证明过程或演算步骤．

15. 如图，四棱锥 $P - A B C D$ 的底面 $A B C D$ 是矩形， $P D ⊥$ 平面 $A B C D$ ， $P D = D C = 2, A D = 2 \sqrt{2}$ ， $M$ 为 $B C$ 的中点．

(1)、求证： $A M ⊥$ 平面 $P B D$ ；

(2)、求平面 $A B C D$ 与平面 $A P M$ 夹角的余弦值．

查看试题解析
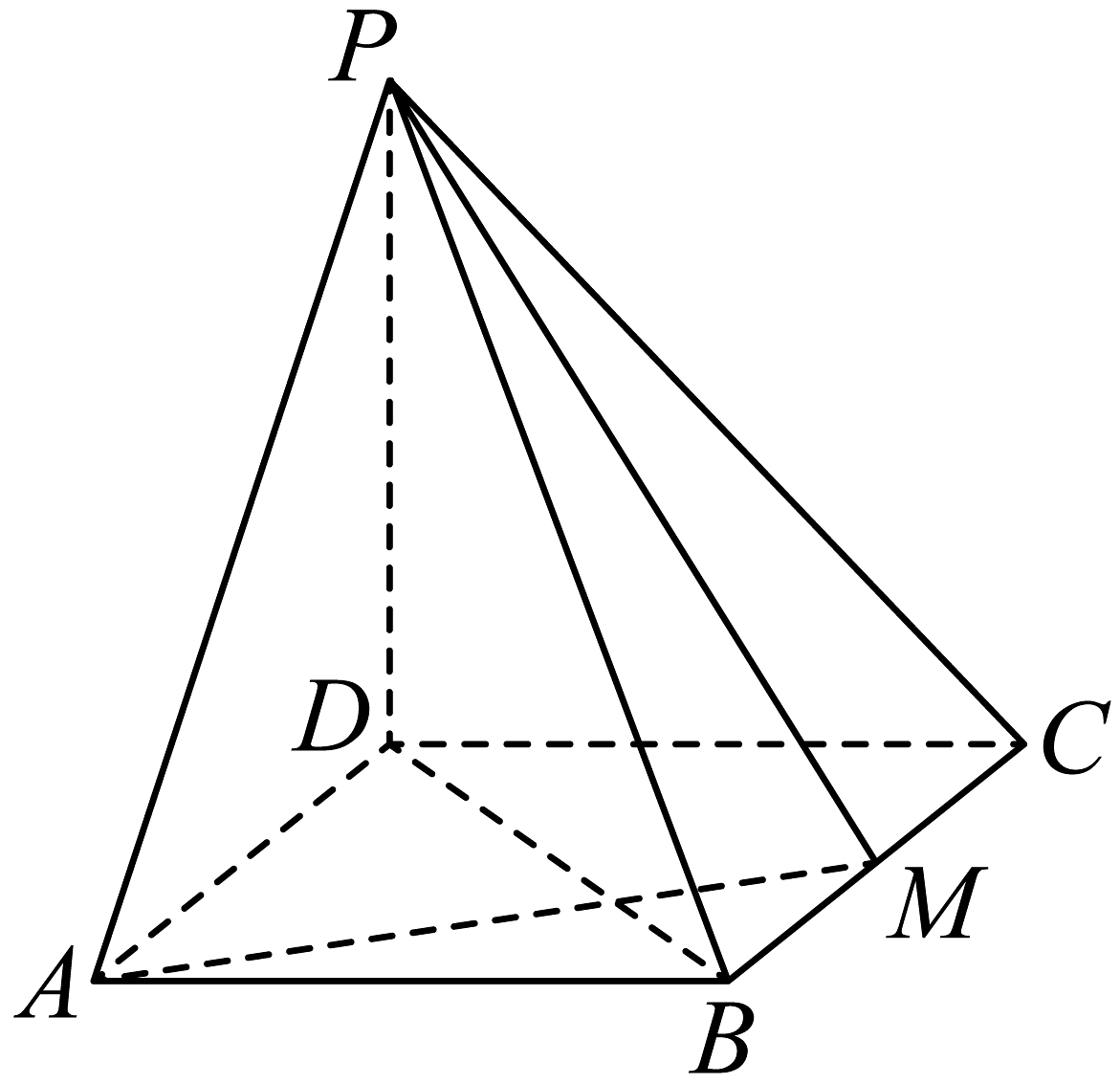16. 为调查学生喜欢在食堂就餐是否和性别有关，学校随机调研了男女生各100人，经统计得到如下 $2 \times 2$ 列联表：

男
女
喜欢
80
40
不喜欢
20
60

(1)、依据 $α = 0.001$ 的独立性检验，判断学生喜欢在食堂就餐是否与性别有关？

(2)、为听取学生对食堂的建议，从学生中抽取9人召开座谈会，并给其中3名同学赠送礼品，每人1份（其余人员仅赠送餐券）．已知参加座谈会的学生中有且只有4名学生来自高一，求高一这4名学生中得到礼品的人数 $X$ 的分布列和数学期望．
$α$
0.010
0.005
0.001
$x_{α}$
6.635
7.879
10.828
附： $χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $(n = a + b + c + d)$

查看试题解析
17. 函数 $f (x)$ 的定义域为 $D$ ，如果 $\forall x \in D$ ，都有 $f (a + x) + f (a - x) = 2 b$ 恒成立，那么 $f (x)$ 的图象关于 $(a, b)$ 对称．已知 $f (x) = x^{3} - 2 a x^{2} + a^{2} x - \frac{2}{27} a^{3}$ ．

(1)、讨论 $f (x)$ 的单调性；

(2)、当 $a = 3$ 时，
①证明：函数 $f (x)$ 图象关于 $(2, 0)$ 对称；
②求 $f (\frac{1}{10}) + f (\frac{2}{10}) + \dots + f (\frac{39}{10})$ 的值．

查看试题解析
18. 某旅游景点统计今年五一期间进入景区的游客人数（单位：千人）如下：
日期
5月1日
5月2日
5月3日
5月4日
5月5日
第 $x$ 天
1
2
3
4
5
参观人数 $y$
2.2
2.6
3.1
5.2
6.9

(1)、根据上表数据，判断成对样本数据 $(x y)$ 的线性相关程度，请用样本相关系数 $r$ 加以说明；（若 $| r | > 0.75$ ，则认为 $y$ 与 $x$ 的线性相关性很强），如果 $y$ 与 $x$ 的线性相关性很强，那么求出 $y$ 关于 $x$ 的经验回归方程；

(2)、五一期间景区开放南门、东门和北门供游客出入，游客从南门、东门和北门进入景区的概率分别为 $\frac{111}{263}$ ，且出景区与入景区选择相同门的概率为 $\frac{2}{3}$ ，选择与入景区不同两门的概率各为 $\frac{1}{6}$ ．假设游客从南门、东门、北门出入景点互不影响，现有甲、乙、丙、丁4名游客于5月1日游玩景点，设 $X$ 为4人中从东门出景区的人数，求 $X$ 的分布列、期望及方差．
附：参考数据： $\sum_{i = 1}^{5} x_{i} y_{i} = 72$ ， $\sum_{i = 1}^{5} x_{i}^{2} = 55$ ， $\bar{y} = 4$ ， $\sum_{i = 1}^{5} y_{i}^{2} = 95.86$ ， $\sqrt{158.6} \approx 12.59$ ．
参考公式：经验回归方程 $\hat{y} = \hat{b} x + \hat{a}$ ，其中 $\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ．
样本相关系数 $r = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sqrt{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}} \sqrt{\sum_{i = 1}^{n} y_{i}^{2} - n {\bar{y}}^{2}}}$ ．

查看试题解析
19. 设 $n \in N^{*}$ ，对任意 $x \in R$ ， $x f_{n}^{'} (x) = (1 - n x) f_{n} (x)$ 成立，则该函数 $f_{n} (x)$ 称为“ $n$ 级函数”，其中 $f_{n}^{'} (x)$ 为函数 $f_{n} (x)$ 的导数．

(1)、判断函数 $y = x e^{k x}$ 和 $y = \frac{x}{e^{k x}}$ ，是否为“ $k$ 级函数”，并说明理由；

(2)、记（1）中的“ $k$ 级函数”为 $g_{k} (x)$ ．
①若 $\exists α, β \in R$ ， $α \neq β$ ，使得 $g_{1} (α) = g_{1} (β)$ ，证明： $α + β > 2$ ；
②若 $\forall x \in (- \frac{1}{2}, 1 - \frac{1}{2} \ln 2)$ ， $g_{2} (x) > \frac{\ln (x + a)}{2 (x + a)}$ ，求实数 $a$ 的取值范围．

查看试题解析

日期	5月1日	5月2日	5月3日	5月4日	5月5日
第 $x$ 天	1	2	3	4	5
参观人数 $y$	2.2	2.6	3.1	5.2	6.9

	男	女
喜欢	80	40
不喜欢	20	60

$α$	0.010	0.005	0.001
$x_{α}$	6.635	7.879	10.828