浙江省宁波市慈溪市2024-2025学年下学期八年级期末数学试题
试卷更新日期：2025-07-16 类型：期末考试
一、选择题（每小题3分，共30分。在每小题给出的四个选项中，只有一项符合题目要求）
-
1. 下列图标中，是中心对称图形的是（ ）A、
B、
C、
D、
2. 下列二次根式中，是最简二次根式的是（ ）A、 B、 C、 D、3. 为落实“双减”政策，增强学生体质，学校开展一分钟跳绳比赛，某7名选手一分钟跳绳个数分别为：182，183，182，194，183，182，195，则这组数据的中位数是（ ）A、182 B、183 C、183.5 D、1844. 用反证法证明命题“若a>b>0，则a2>b2”，首先应假设（ ）A、a2＜b2 B、a2=b2 C、a2≥b2 D、a2≤b25. 如图，在△ABC中，∠C=50°，AC=BC，点D在AC边上，以AB，AD为边作平行四边形ABED，则∠E的度数为（ ）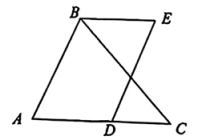
A、50° B、55° C、65° D、70°6. 《九章算术》中记载：“今有户高多于广六尺八寸，两隅相去适一丈，问户高、广各几何？”大意如下：如图，有一形状是矩形的门，它的高比宽多6.8尺，它的对角线长10尺，问它的高与宽各多少？利用方程思想，设矩形门宽为x尺，则依题意所列方程为（ ）
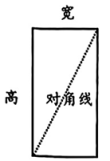A、x2+（x+6.8）2=102 B、x2+（x-6.8）2=102 C、x （x+6.8） =102 D、x（x-6.8）=1027. 若非零实数b，c满足b2=4c，则关于x的一元二次方程x2+bx+c=0的两根之差必为（ ）A、-b B、c C、b+c D、08. 如图，点E是□ABCD边AD上一点（不包含A， D），连接CE，要求用尺规作AF//CE，F是边BC上一点。甲作法：以C为圆心，AE长为半径作弧，交BC于点F，连接AF，则AF//CE。乙作法：以点A为圆心，CE长为半径作弧，交BC于点F，连接AF，则AF//CE。在甲、乙两种作法中，一定正确的是（ ）
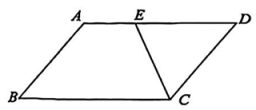A、甲、乙都正确 B、只有甲 C、只有乙 D、甲、乙都不正确9. 已知，点A（a，p），B（a+3，q）在反比例函数y=图象上，则下列说法一定正确的是（ ）A、当a<-3 时，pq<0 B、当a>-3时，pq<0 C、当a>0时， p-q>0 D、当a<0时，p-q>010. 如图，在矩形ABCD中，E，F分别为BC，AD上的点，BE=DF，连结EF，CF，过点D作DG//CF，交EF的延长线于点G，连结CG。若要知道矩形ABCD的面积，则只需要知道下列哪个图形的面积？该图形是（ ）
A、△CEG B、△CEF C、四边形 ECDG D、四边形FCDG二、填空题（每小题3分，共18分）
-
11. 二次根式中，a的取值范围是。12. 一个多边形的内角和是720°，则这个多边形的边数是。13. 若x=1是一元二次方程x2-6x+m=0的根，则方程的另一个根为.14. 如图，D，E分别是△ABC边AB，AC的中点，连接BE，DE。若∠AED=∠BEC，DE=2，则 BE 的长为.
15. 如图，□OABC的边OA在x轴正半轴上，反比例函数y=（k>0， x>0）的图象过□OABC的顶点C和AB的中点D。若□OABC的面积为6，则k的值为。
16. 如图，菱形ABCD，AB=4，∠A=60°。点F、G分别为AB、AD边上的动点，连结FG，将菱形沿FG翻折，点A恰好落在CD边上的点E处。当BF长度最大时，DE的长为。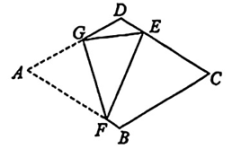
三、解答题（第17、18、19、20、21题各8分，第22、23题各10分，第24题12分，共72分）
-
17. 计算：(1)、；(2)、。18. 解方程：(1)、x2-2x=0；(2)、x2-4x=1219. 我们把顶点在格点的四边形叫做格点四边形。如图在7×7的方格纸中，已知线段AB，请按下列要求完成作图。
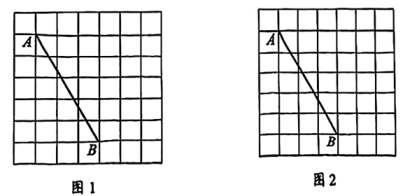(1)、在图1中作格点四边形ABCD，使四边形ABCD为中心对称图形。(2)、在图2中作格点四边形ABCD，使四边形ABCD为轴对称图形。20. 某校八年级同学参加“校史知多少”答题比赛，随机抽查其中20名同学的答题情况，绘制成如图统计图。
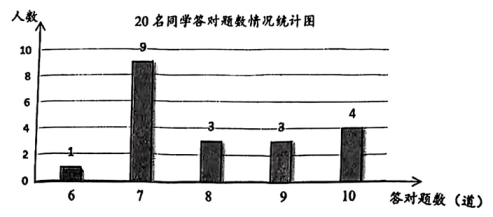(1)、这20名同学的答对题数的众数为道。(2)、求这20名同学的答对题数的平均数。(3)、小明答对了7道题，请分析该成绩在20名同学中处于怎样的水平。21. 如图，一次函数y=x+1和反比例函数y＝（k为常数且k≠0）的图象交于A（-2，m），B两点。
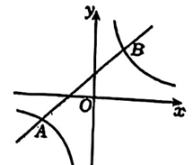(1)、求反比例函数的表达式以及点B的坐标。(2)、利用图象，直接写出不等式x+1>的解。22. 如图，□ABCD，过点A，C分别作AF⊥CD，CE⊥AB，交CD，AB的延长线于点F，E。
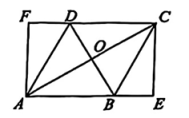(1)、求证：四边形AECF为矩形。(2)、连接AC，BD交于点O，若AC⊥BD，AC= ， BE=2，求矩形AECF的周长。23. 甲同学家有一块空地，空地上有一面长为10米的围墙MN，甲打算利用围墙和木栏围一块长方形养鸡场ABCD，已知木栏总长为50米，与墙相对的一面木栏需开一扇宽为2米的门，门不消耗木栏，设AB长为x米。
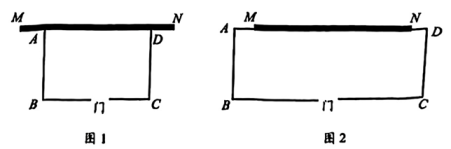(1)、如图1，当AD≤MN时，①AD= 米（用含x的代数式表示）。
②若围成的养鸡场面积为138平方米，求AB的长。
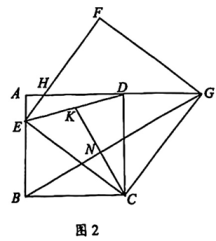
(2)、如图2，当AD>MN时，求养鸡场可达到的最大面积。24. 如图1，边长为4的正方形ABCD，E为AB边上的动点（不与A，B重合），连结CE，以CE为边向右上方作正方形CEFG，边EF与AD交于点H，连结DG。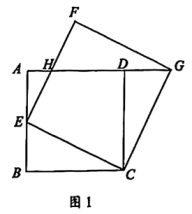
(1)、求证：DG=BE。(2)、若 HD=2DG，求 BE 的长。(3)、如图2，连结BG，过点C作CN⊥BG于点N，交ED于点K。求证：点K为ED的中点。
