四川省成都市武侯区2024-2025学年七年级下学期期末数学试题
试卷更新日期:2025-07-16 类型:期末考试
一、选择题(本大题共10个小题,每小题3分,共30分)
-
1. 以下四款人工智能大模型图标,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 复旦大学成功研制全球首款基于二维半导体材料的32位架构微处理器“无极”,使我国在新一代芯片材料研制中占据先发优势,该芯片在仅有纳米(1纳米米)厚度的二维半导体材料上,通过原子层精准刻蚀技术,实现了5900个晶体管的高密度集成.将数据纳米用科学记数法表示为( )A、米 B、米 C、米 D、米3. 下列计算正确的是( )A、 B、 C、 D、4. 直线a , b , c , d如图所示,在下列条件中,能使的是( )
2. 复旦大学成功研制全球首款基于二维半导体材料的32位架构微处理器“无极”,使我国在新一代芯片材料研制中占据先发优势,该芯片在仅有纳米(1纳米米)厚度的二维半导体材料上,通过原子层精准刻蚀技术,实现了5900个晶体管的高密度集成.将数据纳米用科学记数法表示为( )A、米 B、米 C、米 D、米3. 下列计算正确的是( )A、 B、 C、 D、4. 直线a , b , c , d如图所示,在下列条件中,能使的是( )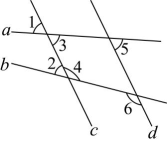 A、 B、 C、 D、5. 在下面各图中,可以近似地刻画一个篮球运动员投出去的球离地面的高度与时间的关系的是( )A、
A、 B、 C、 D、5. 在下面各图中,可以近似地刻画一个篮球运动员投出去的球离地面的高度与时间的关系的是( )A、 B、
B、 C、
C、 D、
D、 6. 小颖想用三根木棒摆成一个三角形,其中两根木棒的长度分别为和 , 则第三根木棒的长度可以是( )A、 B、 C、 D、7. 如图,将直角三角形纸片进行折叠,使得点B恰好落到纸片边缘上的点处,折痕为 , 若 , 则的度数为( )
6. 小颖想用三根木棒摆成一个三角形,其中两根木棒的长度分别为和 , 则第三根木棒的长度可以是( )A、 B、 C、 D、7. 如图,将直角三角形纸片进行折叠,使得点B恰好落到纸片边缘上的点处,折痕为 , 若 , 则的度数为( )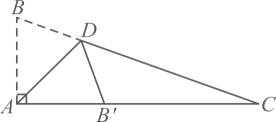 A、 B、 C、 D、8. 下列说法正确的是( )A、“买一张彩票,中奖”是随机事件 B、“将花生油滴入水中,油会浮在水面上”是不可能事件 C、小明做了3次抛瓶盖的试验,其中有2次盖口向上,由此他说盖口向上的概率一定是 D、某射击运动员射击一次只有“中靶”与“不中靶”两种结果,所以他射击一次“中靶”的概率是9. 如图,在等边中,点D , E分别是边的中点,点F是边上一动点,连接 . 当取得最小值时,的度数为( )
A、 B、 C、 D、8. 下列说法正确的是( )A、“买一张彩票,中奖”是随机事件 B、“将花生油滴入水中,油会浮在水面上”是不可能事件 C、小明做了3次抛瓶盖的试验,其中有2次盖口向上,由此他说盖口向上的概率一定是 D、某射击运动员射击一次只有“中靶”与“不中靶”两种结果,所以他射击一次“中靶”的概率是9. 如图,在等边中,点D , E分别是边的中点,点F是边上一动点,连接 . 当取得最小值时,的度数为( )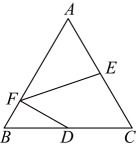 A、 B、 C、 D、10. 已知(),用尺规作图的方法在边上确定一点P , 连接 , 使得 , 则符合要求的作图痕迹是( )A、
A、 B、 C、 D、10. 已知(),用尺规作图的方法在边上确定一点P , 连接 , 使得 , 则符合要求的作图痕迹是( )A、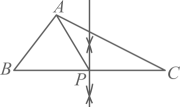 B、
B、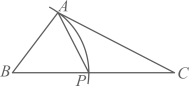 C、
C、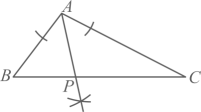 D、
D、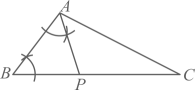
二、填空题(本大题共5个小题,每小题3分,共15分)
-
11. 计算: .12. 在一个不透明的袋子里装有黑、白两种颜色的球共10只,这些球除颜色外都相同.某数学小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:则从袋子中随机摸出一球,这只球是白球的概率是 . (精确到0.1)
摸球的次数n
100
150
200
500
800
1000
摸到白球次数m
58
96
116
295
484
598
摸到白球的频率
0.58
0.64
0.58
0.59
0.605
0.598
13. 如图,将一个含有的三角尺和直尺按如图所示方式摆放在课桌面上,三角尺的角的顶点落在直尺的一边上,若 , 则的度数为 .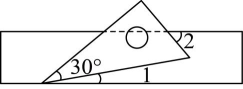 14. 如图,点M是等边三角形内的任意一点,过点M向三边作垂线,垂足分别为D , E , F . 若的边长为6,则的值为 .
14. 如图,点M是等边三角形内的任意一点,过点M向三边作垂线,垂足分别为D , E , F . 若的边长为6,则的值为 .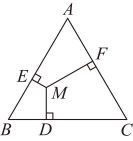 15. 在学习综合与实践《设计自己的运算程序》时,某同学设计了如下运算程序:任意写下一个四位数(四位数字相同的除外),重新排列各位数字,使其组成一个最大的数和一个最小的数,然后用最大的数减去最小的数,得到差,重复这个过程……;现小莉写下一个四位数是 , 按照以上程序进行运算,则第1次得到的差为 , 第100次得到的差为 .
15. 在学习综合与实践《设计自己的运算程序》时,某同学设计了如下运算程序:任意写下一个四位数(四位数字相同的除外),重新排列各位数字,使其组成一个最大的数和一个最小的数,然后用最大的数减去最小的数,得到差,重复这个过程……;现小莉写下一个四位数是 , 按照以上程序进行运算,则第1次得到的差为 , 第100次得到的差为 .三、解答题(本大题共6个小题,共55分)
-
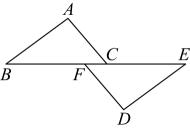
16. 计算(1)、;(2)、 .17.(1)、先化简,再求值: , 其中 , .(2)、已知:如图, , , . 求证: .
 18. 周末,小亮和爸爸相约从家出发去附近的博物馆参观,小亮选择骑自行车前往,先行后,爸爸才开车出发.爸爸行驶一段时间后,停车到商店购买用品,之后以原来倍的速度继续前往目的地,结果二人同时到达博物馆,此时小亮共骑行 . 小亮和爸爸各自行进的路程(单位:)与时间t(单位:)之间的关系如图所示,请结合图象解决下列问题:
18. 周末,小亮和爸爸相约从家出发去附近的博物馆参观,小亮选择骑自行车前往,先行后,爸爸才开车出发.爸爸行驶一段时间后,停车到商店购买用品,之后以原来倍的速度继续前往目的地,结果二人同时到达博物馆,此时小亮共骑行 . 小亮和爸爸各自行进的路程(单位:)与时间t(单位:)之间的关系如图所示,请结合图象解决下列问题: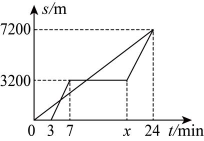 (1)、分别求小亮骑行的速度和爸爸到商店购买用品之前行驶的速度;(2)、求图中x的值;(3)、试问:到达博物馆之前,当t为何值时,小亮和爸爸行进的路程相等?19. 面对一般性的问题时,可以先考虑特殊情形,借助特殊情形下获得的结论或方法解决一般性的问题,这就是特殊化策略.有一个边长为的正方形和腰足够长的等腰直角三角形 , 其中等腰直角三角形的直角顶点与正方形的中心重合.现将等腰直角三角形绕着点进行旋转,请采用特殊化策略探究两个图形重叠部分的面积.
(1)、分别求小亮骑行的速度和爸爸到商店购买用品之前行驶的速度;(2)、求图中x的值;(3)、试问:到达博物馆之前,当t为何值时,小亮和爸爸行进的路程相等?19. 面对一般性的问题时,可以先考虑特殊情形,借助特殊情形下获得的结论或方法解决一般性的问题,这就是特殊化策略.有一个边长为的正方形和腰足够长的等腰直角三角形 , 其中等腰直角三角形的直角顶点与正方形的中心重合.现将等腰直角三角形绕着点进行旋转,请采用特殊化策略探究两个图形重叠部分的面积.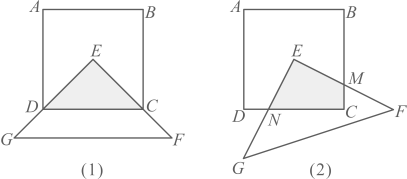 (1)、先考虑特殊情形,如图(),当点 , 分别在边 , 上时,求重叠部分的的面积;(2)、再探究一般情形,如图(),当边 , 分别交边 , 于点 , 时,求重叠部分的四边形的面积.20. “数形结合”是我们在学习中经常用到的一种非常重要的数学思想方法,比如在学习整式的乘法时,我们可以通过构造几何图形数形结合进行分析,用等面积法推理得到多项式的乘法公式.
(1)、先考虑特殊情形,如图(),当点 , 分别在边 , 上时,求重叠部分的的面积;(2)、再探究一般情形,如图(),当边 , 分别交边 , 于点 , 时,求重叠部分的四边形的面积.20. “数形结合”是我们在学习中经常用到的一种非常重要的数学思想方法,比如在学习整式的乘法时,我们可以通过构造几何图形数形结合进行分析,用等面积法推理得到多项式的乘法公式.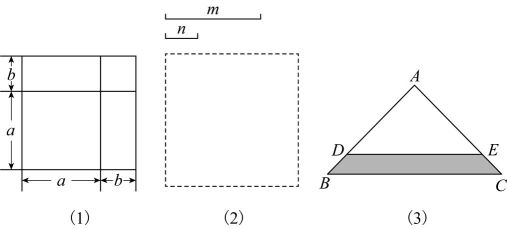 (1)、【初步感知】
(1)、【初步感知】如图(1),我们可以通过构造该图形数形结合进行分析,用等面积法推理得到公式在该公式中,若 , , 求的值;
(2)、【类比探究】如图(2),已知线段m , n , 我们可以根据线段m , n构造几何图形数形结合进行分析,用等面积法推理得到公式请把你构造的几何图形画在虚线框内,并结合该几何图形完成公式的推理过程;
(3)、【拓展应用】如图(3),将两块大小不等的等腰直角三角形尺和等腰直角三角尺重叠摆放,其中D , E分别落在直角边上,若 , , 设 , , 求的值及图中阴影部分的面积.
21. 在中, , .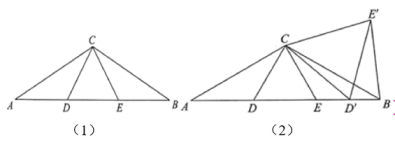 (1)、如图(1),在边上取两点D , E(点D在点E的左侧),连接 , . 当是等边三角形时,求证:;(2)、在(1)的条件下,在线段上取一点(点不与B , E重合),在直线的右侧作等边 , 连接 . 若 , .
(1)、如图(1),在边上取两点D , E(点D在点E的左侧),连接 , . 当是等边三角形时,求证:;(2)、在(1)的条件下,在线段上取一点(点不与B , E重合),在直线的右侧作等边 , 连接 . 若 , .ⅰ)如图(2),当时,求四边形的面积;
ⅱ)请用含n的代数式直接表示出和 , 不必写解答过程.