浙江省绍兴市柯桥区2024-2025学年七年级下学期期末数学试卷

试卷更新日期：2025-07-16 类型：期末考试

进入出卷网下载

一、选择题（每小题2分，共20分）

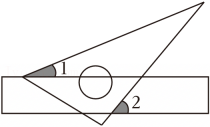
1. 下列运算正确的是（　　）

A、x²•x³＝x⁶ B、（﹣x²）³＝x⁶ C、（x+y）²＝x²+y² D、3x²﹣4x²＝﹣x²

查看试题解析
2. 若 $\frac{x}{x - 3}$ 有意义，则下列说法正确的是（　　）

A、x＞3 B、x≠3 C、x＞3且x≠0 D、x≠0

查看试题解析
3. 在数学活动课上，小丽同学将含30°角的直角三角板的一个顶点按如图方式放置在直尺的一边上，测得∠1＝26°，则∠2的度数是（　　）

A、46° B、64° C、52° D、56°

查看试题解析
4. 下列等式由左边到右边的变形中，属于因式分解的是（　　）

A、（a+1）（a﹣1）＝a²﹣1 B、6x＝2•3x C、x²+2x+1＝x（x+2）+1 D、﹣a²+6a﹣9＝﹣（a﹣3）²

查看试题解析
5. 把分式方程 $\frac{2}{2 x - 4} = \frac{3}{2 x}$ 化为整式方程，方程两边需同时乘以（　　）

A、2x B、2x﹣4 C、2x（x﹣2） D、2x（2x﹣4）

查看试题解析
6. 某校在“爱护水资源”活动中组织学生进行社会调查，并对学生的调查报告进行了评比，如图是将某年级60篇学生调查报告的成绩进行整理，分成5组画出的频率分布条形图．已知从左至右4个小组的频率分别是0.05，0.15，0.35，0.30．那么在这次评比中，被评为优秀的调查报告有（分数大于或等于80分为优秀，且分数为整数）（　　）

A、27篇 B、25篇 C、24篇 D、18篇

查看试题解析
7. 在多项式4x²+1中，添加一个单项式使其成为一个整式的完全平方，则加上的单项式不可以是（　　）

A、4x B、2x C、﹣4x D、4x⁴

查看试题解析
8. 中国古代的《孙子兵法》中记载了一道广为人知的数学问题：现有一百匹马，一百片瓦，大马一匹可以驮三片瓦，小马三匹可以驮一片瓦，问有多少匹大马和多少匹小马？设有大马x匹，小马y匹，则下列方程正确的是（　　）

A、 $\{\begin{array}{l} x + y = 100 \\ \frac{x}{3} + \frac{y}{3} = 100 \end{array}$ B、 $\{\begin{array}{l} x + y = 100 \\ \frac{x}{3} + 3 y = 100 \end{array}$ C、 $\{\begin{array}{l} x + y = 100 \\ 3 x + \frac{y}{3} = 100 \end{array}$ D、 $\{\begin{array}{l} x + y = 100 \\ 3 x + 3 y = 100 \end{array}$

查看试题解析
9. 作业本中有这样一道题，阅读材料，并完成下列问题：不难求得方程 $x + \frac{1}{x} = 3 + \frac{1}{3}$ 的解是x₁＝3， $x_{2} = \frac{1}{3} ； x + \frac{1}{x} = 4 + \frac{1}{4}$ 的解是x₁＝4， $x_{2} = \frac{1}{4} ； x + \frac{1}{x} = 5 + \frac{1}{5}$ 的解是x₁＝5， $x_{2} = \frac{1}{5}$ ；小涛同学仔细观察上述方程及其解，猜想得到：关于x的方程 $x + \frac{1}{x} = m + \frac{1}{m}$ （m≠0）的解是x₁＝m ， $x_{2} = \frac{1}{m}$ ．并尝试解关于x的方程 $\frac{x^{2} - x + 1}{x - 1} = m + \frac{1}{m - 1}$ ．则小涛同学得到的正确的方程的解为（　　）

A、x₁＝m ， $x_{2} = \frac{1}{m - 1}$ B、x₁＝m ， $x_{2} = \frac{m}{m - 1}$ C、x₁＝m﹣1， $x_{2} = \frac{1}{m - 1}$ D、 $x_{1} = m - 1 ， x_{2} = \frac{m}{m - 1}$

查看试题解析
10. 如果甲同学的语文分数或英语分数至少有一门比乙同学高，则称甲同学不亚于乙同学．在班级45个学生中，如果某同学不亚于其他44人，就称他（她）为“潜力之星”，那么某班45个学生中的“潜力之星”最多可能有（　　）

A、22人 B、23人 C、44人 D、45人

查看试题解析

二、填空题（每小题3分，共18分）

11. 分解因式：4x²﹣1= ．

查看试题解析
12. 已知2^x＝3，2²^y＝5，则2^x^﹣2^y的值为．

查看试题解析
13. 对于任意实数a、b ，定义关于“@”的一种运算：a@b＝2a+b ，例如3@4＝2×3+4＝10．若x@（﹣y）＝3，（2y）@x＝5，则x+y的值为．

查看试题解析
14. 若关于x的分式方程 $\frac{2 x}{x - 1} - 3 = \frac{2 m}{1 - x}$ 有增根，则m＝．

查看试题解析
15. 如图所示，在数学拓展课上，小聪将直角三角形纸片ABC（∠A＝25°，∠B＝65°）沿DE向上折叠，点A落在点A'处，当DA'∥BC时，∠DEC＝度．

查看试题解析
16. 对任意一个三位数n ，如果n满足各个数位上的数字互不相同，且都不为零，那么称这个数为“相异数”，将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数，把这三个新三位数的和与111的商记为F（n）．例如n＝123，对调百位与十位上的数字得到213，对调百位与个位上的数字得到321，对调十位与个位上的数字得到132，这三个新三位数的和为213+321+132＝666，666÷111＝6，所以F（123）＝6．
⑴计算：F（124）＝；
⑵若s ， t都是“相异数”，其中s＝100x+32，t＝150+y（1≤x≤9，1≤y≤9，x ， y都是正整数），规定：k $= \frac{F (s)}{F (t)}$ ，当F（s）+F（t）＝16时，则k的值是．

查看试题解析

三、解答题（本大题共有8小题，共62分）

17. 计算下列各题：

(1)、 $(2 - π)^{0} + (- \frac{1}{4})^{- 1}$ ；

(2)、（x﹣3）²﹣（2﹣x）（2+x）．

查看试题解析
18. 解方程（组）：

(1)、 $\{\begin{array}{l} 2 x + y = 7 \\ 5 x + 3 y = 31 \end{array}$ ；

(2)、 $\frac{x - 1}{x - 2} = \frac{3}{2 - x} - 1$ ．

查看试题解析
19. 因式分解：

(1)、ab﹣2a²b+a³b；

(2)、（a﹣b）²+b﹣a ．

查看试题解析
20. 先化简，再求值： $(a + 1 - \frac{3}{a - 1}) \div \frac{a^{2} + 4 a + 4}{a - 1}$ ，其中a＝4．

查看试题解析
21. 学校为了丰富课后服务内容，欲增加一些体育专项课程，为此对该校一部分学生进行了一次“你最喜欢的项目”问卷调查（每人只选一项）．根据收集到的数据，绘制成如下两幅不完整的统计图，请根据图中提供的信息，完成下列问题：

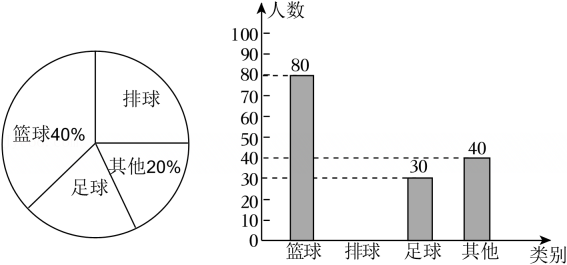(1)、在这次问卷调查中，共调查了多少名学生？

(2)、求在扇形统计图中，喜欢“足球”的所占的圆心角度数；

(3)、如果全校共有学生2000名，请估计该校最喜欢“排球”的学生约有多少人？

查看试题解析
22. 已知：如图点C在∠MON的一边OM上，过点C的直线AB∥ON ， CD平分∠OCB ， CE⊥CD ．

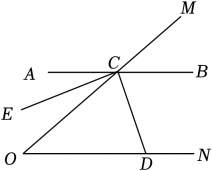(1)、若∠O＝40°，求∠BCD的度数；

(2)、求证：CE平分∠OCA ．

查看试题解析

23. 根据以下素材，完成任务．

素材一	为促进消费，某旅行社推出“柯桥古镇一日游”活动，收费标准如下：
	人数a	0＜a≤100	100＜a≤200	a＞200
	收费标准（元/人）	6x	85	5x
素材二	A、D公司人数少于100人，B公司人数多于200人，C公司人数多于100人，A公司比B公司少160人．
素材三	A、B、C、D四个公司分别各自参加此项活动，经核算，A公司共花费7200元，B公司共花费18000元；C公司和D公司共花费18270元，若C、D公司联合组团只需花费17850元．
任务一	求x的值．
任务二	C公司和D公司分别有多少人？

查看试题解析

24. 一般情况下，一个分式通过适当的变形，我们可以把它化成一个整式和一个分子是整数的分式的和的形式，例如：
① $\frac{x + 1}{x - 1} = \frac{(x - 1) + 2}{x - 1} = 1 + \frac{2}{x - 1}$ ；
② $\frac{x^{2}}{x - 2} = \frac{x^{2} - 4 + 4}{x - 2} = \frac{(x + 2) (x - 2) + 4}{x - 2} = (x + 2) + \frac{4}{x - 2}$ ；
③ $\frac{x^{3}}{x - 1} = \frac{x^{3} - x^{2} + x^{2}}{x - 1} = x^{2} + \frac{x^{2}}{x - 1} = \dots$

(1)、仿照上述方法，试将分式 $\frac{x + 7}{x + 3} ， \frac{2 x^{2} - 1}{x + 1}$ 化为一个整式和一个分子是整数的分式的和的形式；

(2)、仿照上述方法，把 $\frac{x^{3}}{x + 3}$ 化成一个整式和一个分子是整数的分式的和的形式；

(3)、已知x、y均为正整数， $M = \frac{x}{x - 5} ， N = \frac{7 y}{7 y - 5}$ ，且M、N均为正数．若M+N＝3，请求出x、y的值．

查看试题解析