广东省深圳市龙华区2024-2025学年八年级下学期期末数学试题

试卷更新日期：2025-07-16 类型：期末考试

进入出卷网下载

一、选择题（本题共有8小题，每小题3分，共24分，每小题有四个选项，其中只有一个是正确的）

1. 对称性不仅是数学的美学体现，更是生物适应环境的“最优解”。下列生物的外轮廓同时
具备轴对称性和中心对称性的是（）

A、 B、 C、 D、

查看试题解析
2. 下列x的值是不等式x-1>0的解的是（）

A、x=2 B、x=1 C、x=0 D、x=-1

查看试题解析
3. 分式 $\frac{x - 1}{x + 2}$ 的值为0的条件是（）

A、x=-2 B、x=-1 C、x=1 D、x=2

查看试题解析
4. 将图①沿虚线剪开后，拼成如图②所示的长方形，据此写出一个多项式的因式分解为（）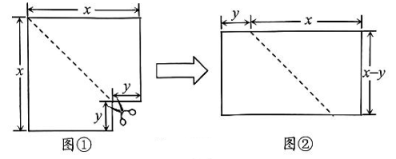

A、x²-y²=(x+y)(x-y) B、x²+y²=(x+y) (x-y) C、(x+y) (х-y)=x²-y² D、(x+y)(x-y)=x²+y²

查看试题解析
5. 如图，三条公路两两相交，现计划修建一个油库，要求油库到这三条公路（AB，AC，BC) 的距离都相等，则油库的位置可以设计在（）

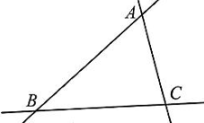A、△ABC三条中线的交点 B、△ABC三条角平分线的交点 C、△ABC三条高所在直线的交点 D、△ABC三条边的垂直平分线的交点

查看试题解析
6. 藻井作为中国传统建筑中独特的穹顶装饰构件，其造型融合宇宙观，仅用于最高等级建筑，并巧妙结合五行思想。如图是外轮廓为正八边形的“蟠龙藻井”图案，这个正八边形的每个内角的度数为（）

A、45° B、120° C、130° D、135°

查看试题解析
7. 今有绫、罗共三丈，各值钱八百九十六文。只云绫、罗各一尺共值钱一百二十文，问绫、罗尺价各几何？（选自《四元玉鉴》）题目大意：现在有绫和罗一共3丈（1丈=10尺），它们各自的价值都是896文钱。已知绫和罗各1尺总共值120文钱，问绫和罗每尺的价值各多少钱？设绫布有x尺，根据题意可列方程为（）

A、 $\frac{896}{3 - x} + \frac{896}{x} = 120$ B、 $\frac{896}{120 - x} + \frac{896}{x} = 30$ C、 $\frac{896}{30 - x} + \frac{896}{x} = 120$ D、 $\frac{896}{120 - x} + \frac{896}{x} = 3$

查看试题解析
8. 如图，在平面内将一块含45°的三角板ABC向右平移得到ADEF，若∠BAD=30°，则边BC扫过的面积与边AB扫过的面积之比为（）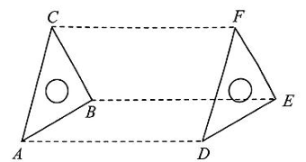

A、2 B、 $\sqrt{3}$ C、 $\sqrt{2}$ D、 $\frac{2 \sqrt{3}}{3}$

查看试题解析

二、填空题（本题共有5小题，每小题3分，共15分。）

9. 因式分解： $x^{2} y + 2 x y + y$ = ．

查看试题解析
10. A、B两地相距10千米，甲从A地到B地步行需要t小时，乙骑自行车行同样的路程比甲少用1小时，则乙的速度可表示为千米/时。

查看试题解析
11. 关于 x 的不等式组 ${\begin{array}{l} x \geq a \\ x \geq 1 \end{array}$ 的解集为 $x \geq 1$ ，请写出一个符合条件的 a 的值：。

查看试题解析
12. 如图，将两个完全相同的直角三角形纸板叠放在一起， $∠ A = ∠ F = 3 0^{°}$ 。若 $B D = \sqrt{3}$ ，则CE的长度为。

查看试题解析
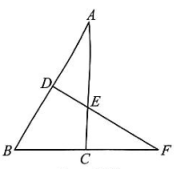13. 如图，D是等边△ABC内一点，∠ADC=120°，CD=6，则△BDC的面积为.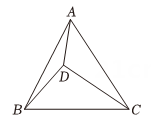

查看试题解析

三、解答题（本大题共7小题，共61分）

14.

(1)、解不等式组 ${\begin{array}{l} 2 x < - 4, \\ x + 1 > \frac{x - 1}{2} \end{array}$

(2)、先化简，再求值： $(\frac{2 m - 1}{m} - 1) \div \frac{m^{2} - 1}{m^{2} + 2 m}$ ，其中 $m = 2$ 。

查看试题解析
15. 如图，在方格纸中，每个小方格的边长均为1个单位长度，线段AB的两个端点都在小方格的格点上，根据下列要求用无刻度直尺作图：

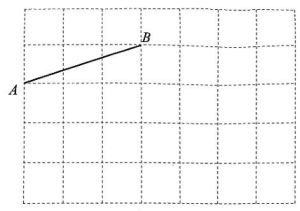(1)、将线段AB绕点B逆时针旋转90得到线段BD；

(2)、平移线段AB至线段DC，使得点A与点D重合，连接AD，BC；

(3)、直线BD将四边形ABCD分成了全等的两个部分，这样的直线还有很多，请再画出
两条符合条件的直线。

查看试题解析
16. 如图，在△ABC中，AB=AC，点D，E都在边BC上，且AD=AE。请判断BD与CE之间的数量关系，并说明理由。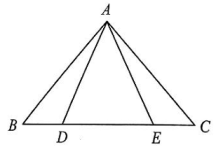

查看试题解析
17. 小亮计划去书店为全班50名同学各买一本课外书，从书店店员处了解到，科普书的单价是文学书的单价的1.5倍，若用150元分别购买这两种书，所买的科普书比所买的文学书少5本。

(1)、科普书和文学书的单价各是多少元？

(2)、若小亮可以使用的经费不超过700元，则至多购买多少本科普书？

查看试题解析
18. 如图，在□ABCD中，AP⊥BD于点P。请用尺规作图在BD上求作一点Q，连接AQ，CQ，PC，使得四边形APCQ是平行四边形。

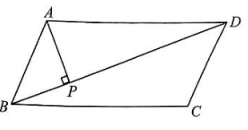(1)、某数学小组经过讨论，得到如下两种作法，请选择其中一种作法说明其正确性。
思路一
思路二
作图步骤
在 BD上作 DQ=BP。点Q即为所求。
过点C作CQ⊥BD于点Q。点Q即为所求。
作图痕迹
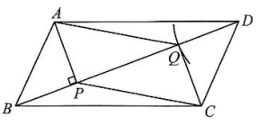
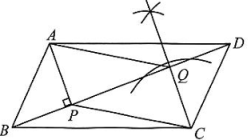
我选择思路 ▲ ，理由如下：

(2)、请你用不同于（1）中的尺规作图方法求作出点Q（保留作图痕迹，不写作法），并说明作法的正确性。

查看试题解析
19. 数学学习小组在学习《不等关系》后，深入研究了两个正数a，b的和与积之间的大小关系。
【发现问题】当a=b=2时，a+b=ab。
【提出问题】当a>2，b>2时，a+b与ab存在怎样的大小关系？

(1)、【特例分析】给a，b分别赋予不同的数值，通过计算，判断a+b与ab的大小关系。
请完成下面的表格：
a
…
3
4
5
…
b
…
3
5
6
…
a+bab
（填“>”，“＜”、"=”）
…
＜
＜
…

(2)、【得出猜想】根据特例分析，猜想：当a>2，b>2时，a+bab。

(3)、【验证猜想】
①小明认为可以设a=2+x，b=2+y，其中x>0，y>0，再通过计算完成验证。
请补充验证过程：
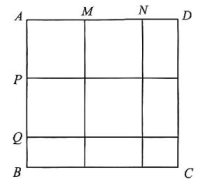
②小红发现可以用图形的面积关系来直观验证。
如图，在长方形ABCD中，AB=a>2，AD=b>2，AM=MN=AP=PQ=1。请在长方形ABCD中，用画阴影的方法表示面积为(a+b)的部分。

(4)、【深入探究】学习小组经过讨论，还可从以下思路验证猜想：
思路一：利用不等式的基本性质得到 $a b > 2 b ⋯$
思路二：对多项式 $(a b - a - b + 1)$ 进行因式分解 $⋯$
思路三：对分式 $\frac{a + b}{a b}$ 进行变形与运算 $⋯$
根据以上思路的启发，选择一种方法完成验证。

查看试题解析
20. 综合与实践
数学活动课上，同学们对两个完全相同的直角三角形纸片（如图1）围绕拼接、平移、旋转开展操作研究。

(1)、【活动一】拼接
将两个三角形纸片按图2方式进行拼接（点A与点F重合，点C与点D重合），求四边形ABCE的周长；

(2)、【活动二】平移
在图2中，将△ABC纸片沿射线FE的方向平移。在平移过程中，两个纸片的重叠部分为四边形AMDN，如图3所示。
①求证：四边形AMDN是平行四边形；
②若点A为EF的中点，则四边形AMDN的周长为 ▲ 。

(3)、【活动三】旋转
在图3中，当点A为EF的中点时，将△DEF绕点F顺时针旋转一周。在旋转过程中，若两个纸片的重叠部分为等腰三角形，直接写出旋转角的度数。

查看试题解析

	思路一	思路二
作图步骤	在 BD上作 DQ=BP。点Q即为所求。	过点C作CQ⊥BD于点Q。点Q即为所求。
作图痕迹