广东省深圳市2024-2025学年八年级下学期期末数学试卷
试卷更新日期:2025-07-16 类型:期末考试
一、选择题:本题共8小题,每小题3分,共24分.在每小题给出的选项中,只有一项是符合题目要求的.
-
1. 第33届夏季奥林匹克运动会于2024年7月26日月11日在法国巴黎如期举行.以下是巴黎奥运会部分比赛项目的图标,其中是中心对称图形的是( )A、
 皮划艇
B、
皮划艇
B、 柔道
C、
柔道
C、 游泳
D、
游泳
D、 击剑
2. 下列因式分解正确的是( )A、 B、 C、 D、3. 在中, , , 分别以点A、B为圆心,以大于的长为半径画弧,两弧分别交于点M、N,作直线交点D,连接 , 则的大小是( )
击剑
2. 下列因式分解正确的是( )A、 B、 C、 D、3. 在中, , , 分别以点A、B为圆心,以大于的长为半径画弧,两弧分别交于点M、N,作直线交点D,连接 , 则的大小是( ) A、 B、 C、 D、4. 不等式的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、4. 不等式的解集在数轴上表示正确的是( )A、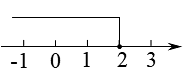 B、
B、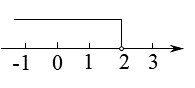 C、
C、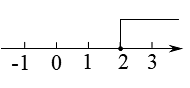 D、
D、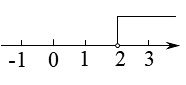 5. 如图,若两个三角形全等,图中字母表示三角形边长,则的度数为( )
5. 如图,若两个三角形全等,图中字母表示三角形边长,则的度数为( ) A、 B、 C、 D、6. 如图,AB、CD是两面平行放置的平面镜,一束光线MP在点P处经平面镜CD反射后得到光线PN,PN在点N处经平面镜AB反射后得到光线NQ,已知 , , 若 , 则的度数为( )
A、 B、 C、 D、6. 如图,AB、CD是两面平行放置的平面镜,一束光线MP在点P处经平面镜CD反射后得到光线PN,PN在点N处经平面镜AB反射后得到光线NQ,已知 , , 若 , 则的度数为( )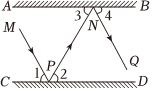 A、 B、 C、 D、7. 某市开展“悦读书,与心共鸣”读书活动,甲、乙两位同学分别从距离活动地点1400m和900m的两地同时出发,参加活动,甲同学的速度是乙同学的1.1倍,乙同学比甲同学提前7min到达活动地点,若设乙同学的速度是xm/min,则下列方程正确的是( )A、 B、 C、 D、8. 如图,将绕点A按顺时针旋转一定角度得到 , 点的对应点D恰好落在BC边上.若 , , 则CD的长为( )
A、 B、 C、 D、7. 某市开展“悦读书,与心共鸣”读书活动,甲、乙两位同学分别从距离活动地点1400m和900m的两地同时出发,参加活动,甲同学的速度是乙同学的1.1倍,乙同学比甲同学提前7min到达活动地点,若设乙同学的速度是xm/min,则下列方程正确的是( )A、 B、 C、 D、8. 如图,将绕点A按顺时针旋转一定角度得到 , 点的对应点D恰好落在BC边上.若 , , 则CD的长为( )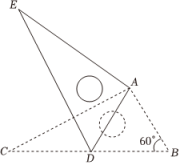 A、3 B、 C、6 D、
A、3 B、 C、6 D、二、填空题:本题共5小题,每小题3分,共15分.
-
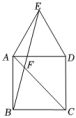
9. 如图,在正方形ABCD外侧,以AD为一边向上作等边三角形ADE,连接BE,AC,相交于点F,则的度数是.
 10. 若分式的值为零,则的值是 .11. 如图,圆锥的底面半径为3,高为4,则该圆锥的侧面积为.
10. 若分式的值为零,则的值是 .11. 如图,圆锥的底面半径为3,高为4,则该圆锥的侧面积为.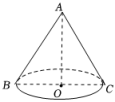 12. 如图,中, , BD是的角平分线,点D在AB的垂直平分线上,若 , 则.
12. 如图,中, , BD是的角平分线,点D在AB的垂直平分线上,若 , 则.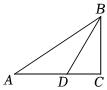 13. 为落实劳动素质教育,推动学生劳动实践的有效进行,某校在校园开辟了劳动实践基地.如图是从实践基地抽象出来的几何模型:两块边长分别为m,n的正方形且 , 其中重叠部分B为池塘,阴影部分 , 分别表示七年级和八年级的实践活动基地面积.若 , , 则 .
13. 为落实劳动素质教育,推动学生劳动实践的有效进行,某校在校园开辟了劳动实践基地.如图是从实践基地抽象出来的几何模型:两块边长分别为m,n的正方形且 , 其中重叠部分B为池塘,阴影部分 , 分别表示七年级和八年级的实践活动基地面积.若 , , 则 .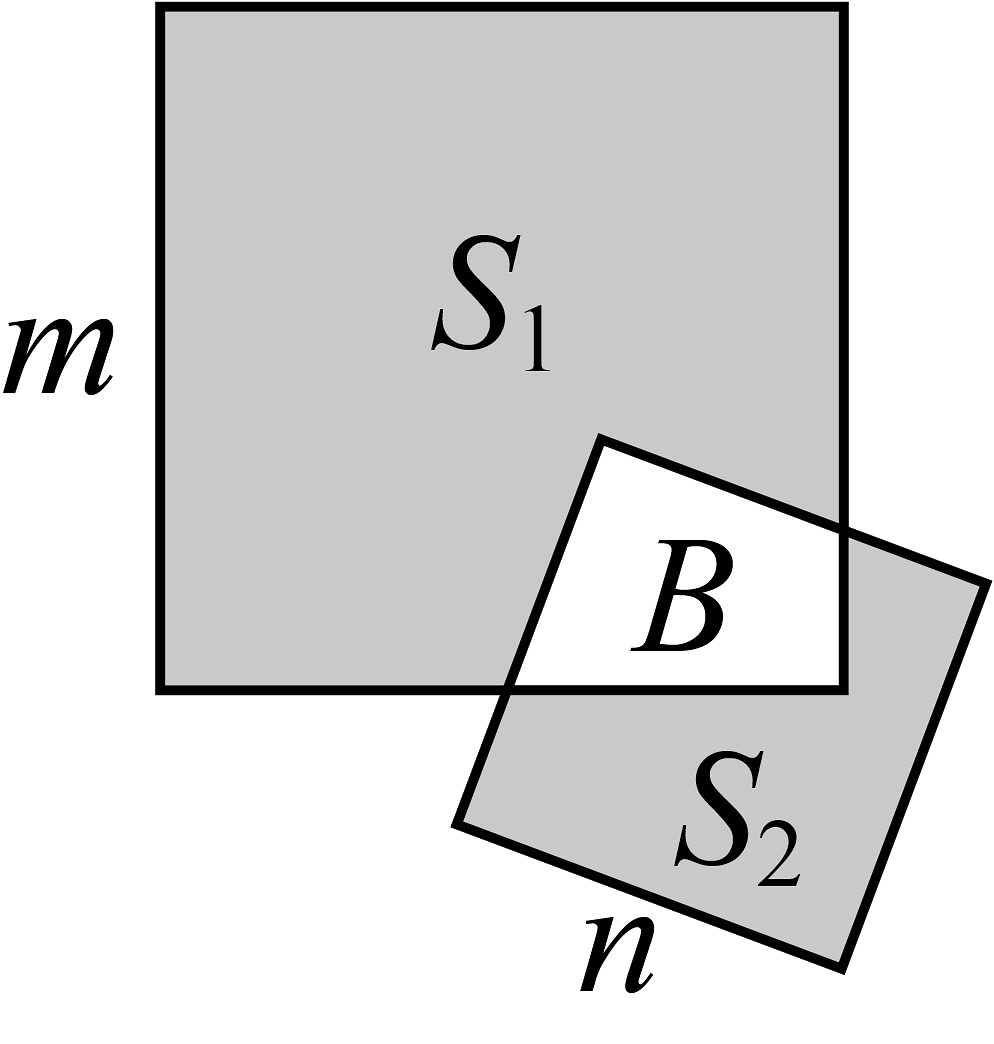
三、解答题:本题共7小题,共61分.解答应写出文字说明,证明过程或演算步骤.
-
14. 分解因式:(1)、;(2)、 .15. 已知先在A,B,C中任选2个分式用除号“”连接并进行化简,再从0,1,2中选择一个合适的数作为x的值代入求值.16. 如图,在平面直角坐标系中,的三个顶点A,B,C的坐标分别为 , , , 将向左平移3个单位长度,再向下平移4个单位长度得到
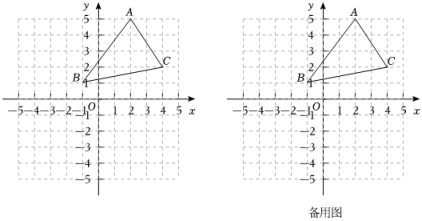 (1)、画出平移后的并写出 , , 的坐标;(2)、内部一点的坐标为 , 写出平移前点的对应点P的坐标.(3)、连接线段 , 请在x轴上找一点G,使得的面积为8,直接写出满足条件的点G坐标.17. 某商店销售A、B两种型号的打印机,销售3台A型和2台B型打印机的利润和为560元,销售1台A型和4台B型打印机的利润和为720元.(1)、求每台A型和B型打印机的销售利润;(2)、商店计划购进A、B两种型号的打印机共120台,其中A型打印机数量不少于B型打印机数量的一半,设购进A型打印机a台,这120台打印机的销售总利润为w元,求该商店购进A、B两种型号的打印机各多少台,才能使销售总利润最大?(3)、在的条件下,厂家为了给商家优惠让利,将A型打印机的出厂价下调m元 , 但限定商店最多购进A型打印机50台,且A、B两种型号的打印机的销售价均不变,请写出商店销售这120台打印机总利润最大的进货方案.18. 已知:在中, , , , 点D,E分别是BC,AD的中点, , 交CE的延长线于
(1)、画出平移后的并写出 , , 的坐标;(2)、内部一点的坐标为 , 写出平移前点的对应点P的坐标.(3)、连接线段 , 请在x轴上找一点G,使得的面积为8,直接写出满足条件的点G坐标.17. 某商店销售A、B两种型号的打印机,销售3台A型和2台B型打印机的利润和为560元,销售1台A型和4台B型打印机的利润和为720元.(1)、求每台A型和B型打印机的销售利润;(2)、商店计划购进A、B两种型号的打印机共120台,其中A型打印机数量不少于B型打印机数量的一半,设购进A型打印机a台,这120台打印机的销售总利润为w元,求该商店购进A、B两种型号的打印机各多少台,才能使销售总利润最大?(3)、在的条件下,厂家为了给商家优惠让利,将A型打印机的出厂价下调m元 , 但限定商店最多购进A型打印机50台,且A、B两种型号的打印机的销售价均不变,请写出商店销售这120台打印机总利润最大的进货方案.18. 已知:在中, , , , 点D,E分别是BC,AD的中点, , 交CE的延长线于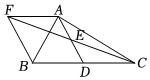 (1)、求证:四边形AFBD为平行四边形;(2)、求四边形AFBD的面积.19. 【背景】如图1是某品牌的饮水机,此饮水机有开水、温水两个按钮,图2为其信息图.
(1)、求证:四边形AFBD为平行四边形;(2)、求四边形AFBD的面积.19. 【背景】如图1是某品牌的饮水机,此饮水机有开水、温水两个按钮,图2为其信息图.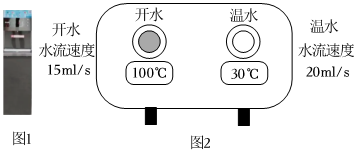
【主题】如何接到最佳温度的温水.
【素材】水杯容积:
物理知识:开水和温水混合时会发生热传递,开水放出的热量等于温水吸收的热量.即:开水体积开水降低的温度=温水体积温水升高的温度.
生活经验:饮水最佳温度是包括与 , 这一温度最接近人体体温.
【操作】先从饮水机接温水x秒,再接开水,直至接满700ml的水杯为止.
备注:接水期间不计热损失,不考虑水溢出的情况
【问题】
(1)、接到温水的体积是ml,接到开水的体积是ml;用含x的代数式表示(2)、若所接的温水的体积不少于开水体积的2倍,则至少应接温水多少秒?(3)、若水杯接满水后,水杯中温度是 , 求x的值;(4)、记水杯接满水后水杯中温度为 , 则y关于x的关系式是;若要使杯中温度达到最佳水温,直接写出x的取值范围是.20. 如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中 ,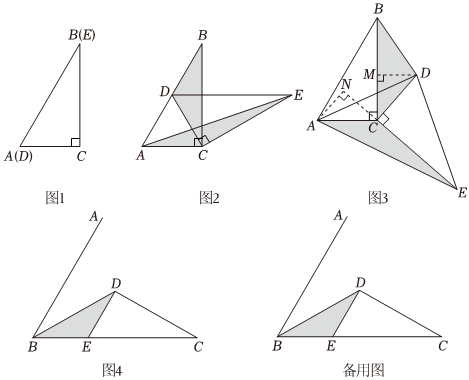 (1)、【操作发现】
(1)、【操作发现】如图2,固定 , 使绕点C旋转,点D恰好落在AB边上时,填空:
①;
②设的面积为 , 的面积为 , 则与的数量关系是.
(2)、【猜想论证】当在如图3所示的位置时,小明猜想中与的数量关系仍然成立,并尝试分别作出了和中BC、CE边上的高,请你证明小明的猜想.
(3)、【拓展探究】已知 , 点D是角平分线上一点, , 交BC于点如图若在射线BA上存在点F,使 , 请求出的度数.