广西来宾市2024-2025学年七年级下学期期末考试数学试题
试卷更新日期:2025-07-02 类型:期末考试
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项符合题目要求.
-
1. 下列标志图形中,( )不是轴对称图形.A、
 B、
B、 C、
C、 D、
D、 2. ( )A、 B、 C、 D、3. 下列各数中,( )是无理数.A、 B、 C、 D、4. 已知 , , 则的值为( )A、9 B、18 C、3 D、25. 若 , 则下列不等式正确的是( )A、 B、 C、 D、6. 若是完全平方差公式,则( )A、 B、 C、4 D、87. 规定 , 若 , 则( )A、2 B、4 C、6 D、88. 已知三角形的三个内角的度数之和是 , 现将两个三角板按如图摆放,其中 , , , 那么( )
2. ( )A、 B、 C、 D、3. 下列各数中,( )是无理数.A、 B、 C、 D、4. 已知 , , 则的值为( )A、9 B、18 C、3 D、25. 若 , 则下列不等式正确的是( )A、 B、 C、 D、6. 若是完全平方差公式,则( )A、 B、 C、4 D、87. 规定 , 若 , 则( )A、2 B、4 C、6 D、88. 已知三角形的三个内角的度数之和是 , 现将两个三角板按如图摆放,其中 , , , 那么( )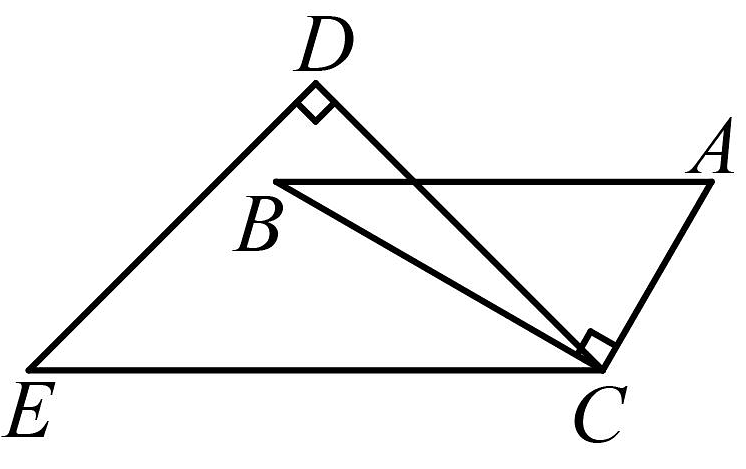 A、 B、 C、 D、9. 我市某中学调查七年级学生课外阅读情况,统计如下表:
A、 B、 C、 D、9. 我市某中学调查七年级学生课外阅读情况,统计如下表:阅读时间
人数
2小时以下
25
2~4小时
15
4小时以上
10
则“4小时以上”所占百分比是( )
A、 B、 C、 D、10. 某校积极响应加快建设体育强国的号召,学校体育室将购买篮球和排球共20个,已知篮球售价80元/个,排球售价60元/个.已知购买篮球和排球的总费用不超过1400元,假设购买x个篮球,根据题意可列关于x的不等式为( )A、 B、 C、 D、11. 如图, , 于点 , 交于点 , 于点 , 已知 , 则点到的距离为( )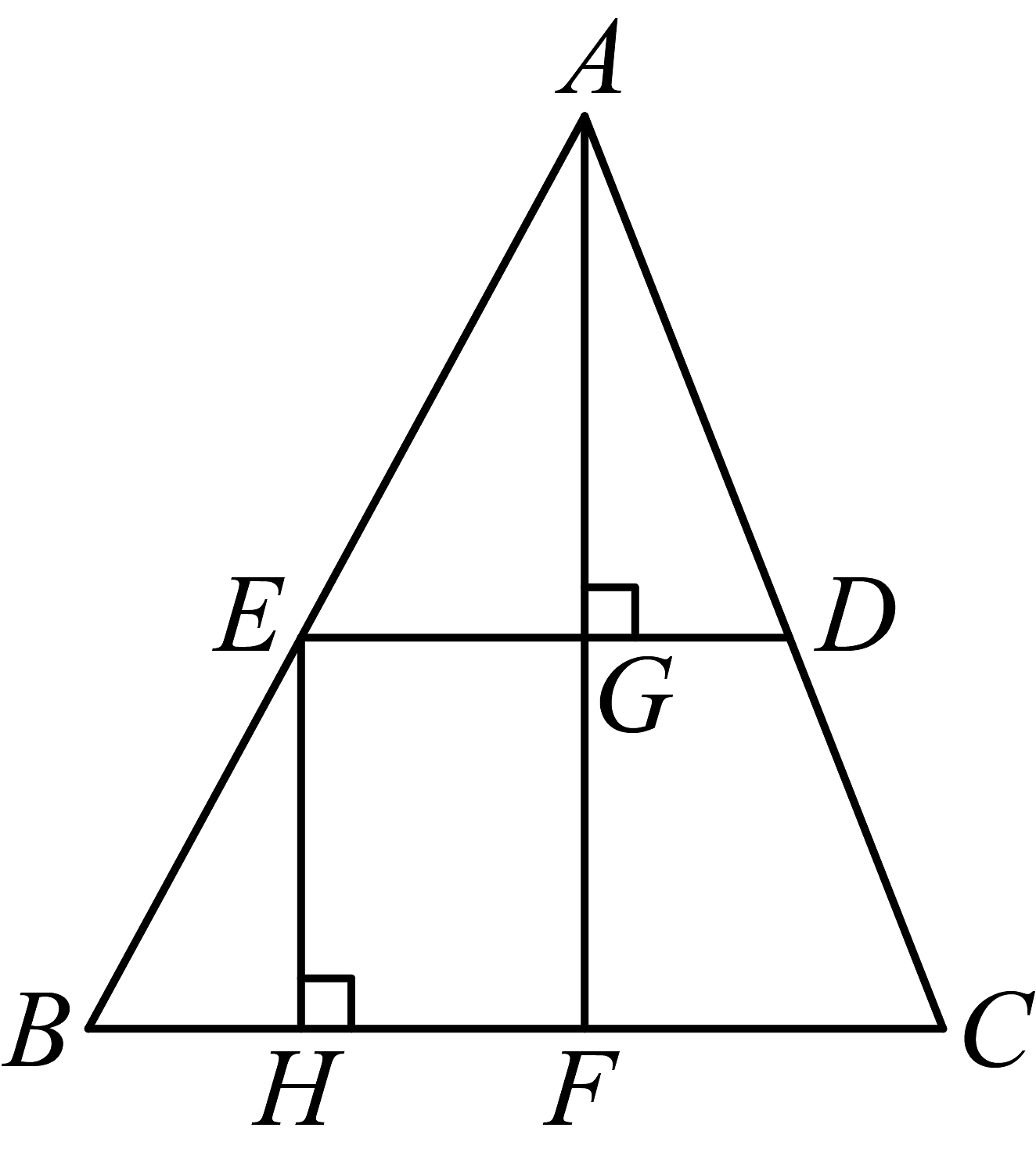 A、2 B、3 C、4 D、512. 如果 , 那么( )A、16 B、14 C、196 D、194
A、2 B、3 C、4 D、512. 如果 , 那么( )A、16 B、14 C、196 D、194二、填空题:本大题共4小题,每小题3分,共12分.
-
13. 将一把剪刀张开一定的角度,则可以构成4个角,将其抽象成一般的几何图形(如图所示),若 , 则 .
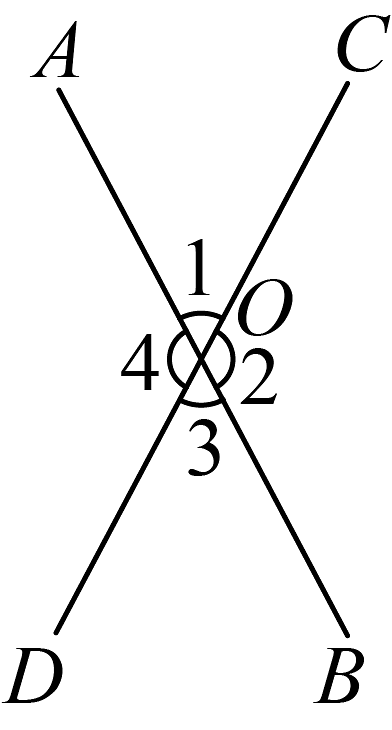 14. 比较两数的大小:4(用“”或“”填空).15. 如图所示,已知圆的半径为 , 则图中阴影部分面积为 .
14. 比较两数的大小:4(用“”或“”填空).15. 如图所示,已知圆的半径为 , 则图中阴影部分面积为 .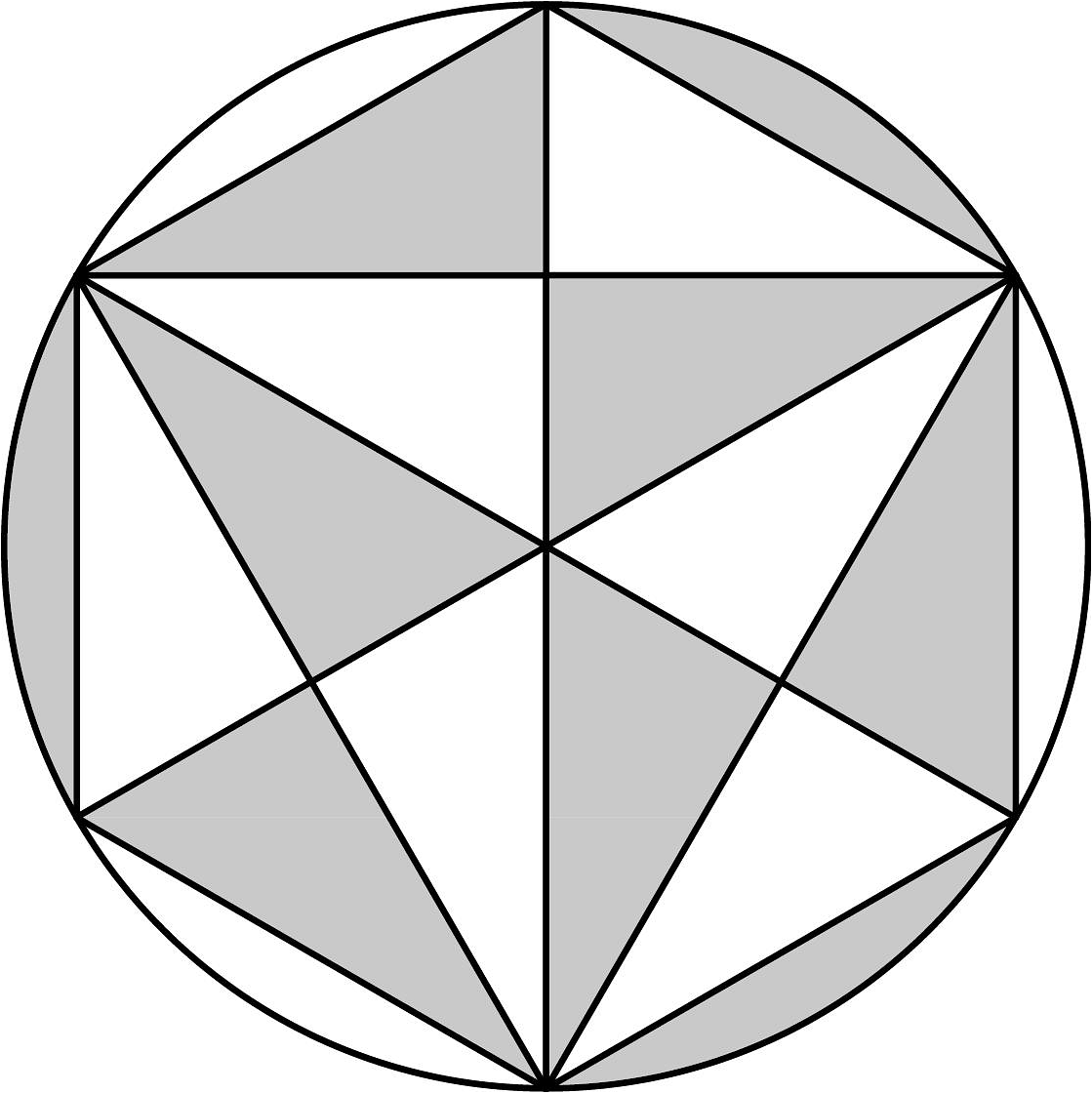 16. 关于的不等式组 , 的解集中任意一个的值都不在的范围内,则的取值范围是 .
16. 关于的不等式组 , 的解集中任意一个的值都不在的范围内,则的取值范围是 .三、解答题:本大题共7小题,共72分.解答应写出文字说明、证明过程或演算步骤.
-
17. 如图,点在点北偏东方向,点在点北偏西方向,且 , 求点到到直线的距离.
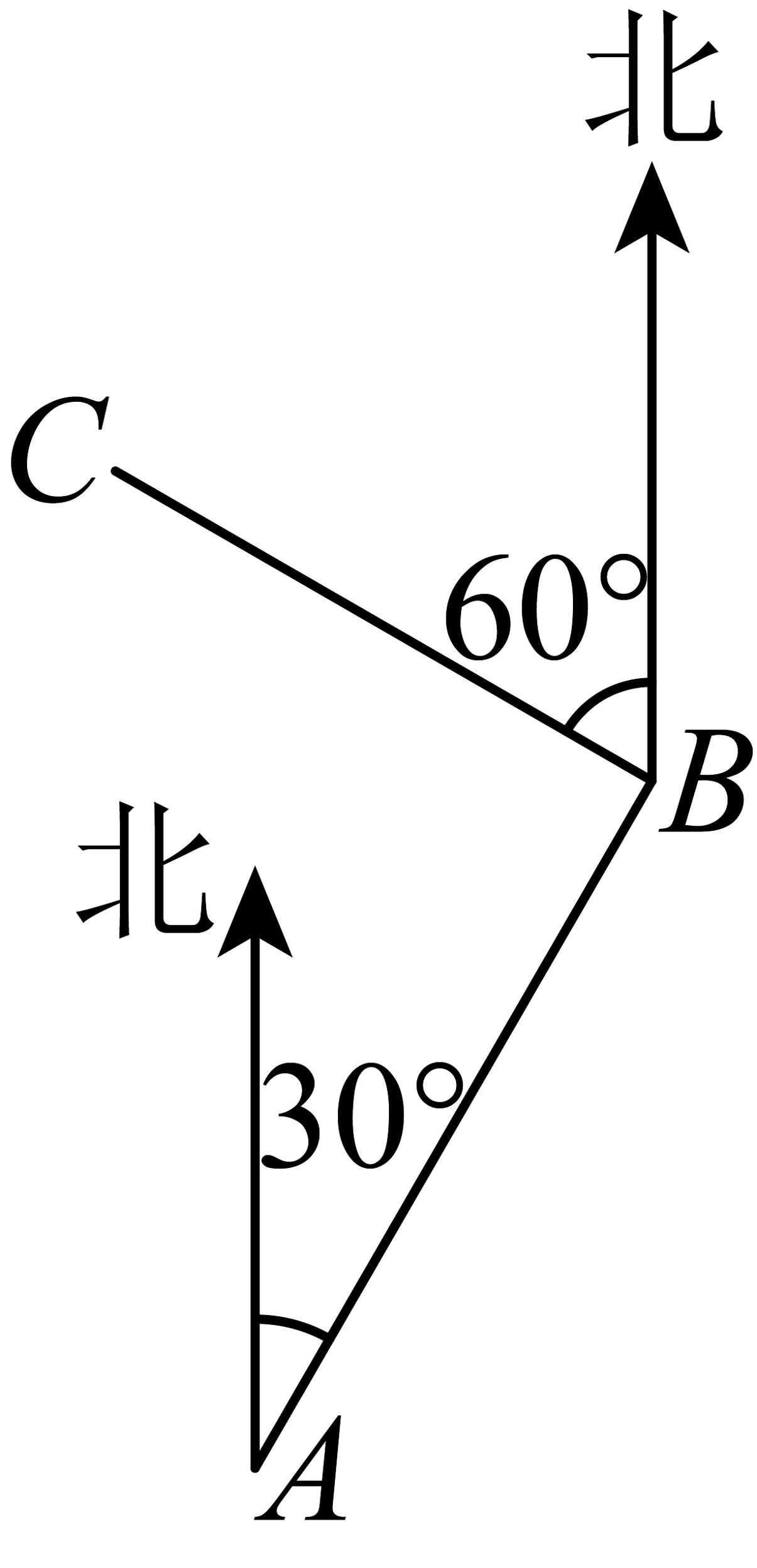 18. (1)计算:;
18. (1)计算:;(2)解不等式 , 并把它的解集在数轴上表示出来.
19. 端午前夕的劳动课上,由于制作香包的需要,小红想用一块面积为的正方形绸布,沿着边的方向裁剪出一块面积为的长方形绸布,使它的长宽比为 . 她不知道能否裁剪出来,正在发愁.小花见了说:“别发愁,一定能用一块面积大的绸布裁剪出一块面积小的绸布.”你赞同小花的说法吗?小红能用这块面积为的正方形绸布载剪出符合要求的绸布吗?请给出理由,根据题意列出数量关系式并解答.20. 如图,在正方形网格中,每个小正方形的边长均为1个单位,的三个顶点都在格点上,请按要求画图: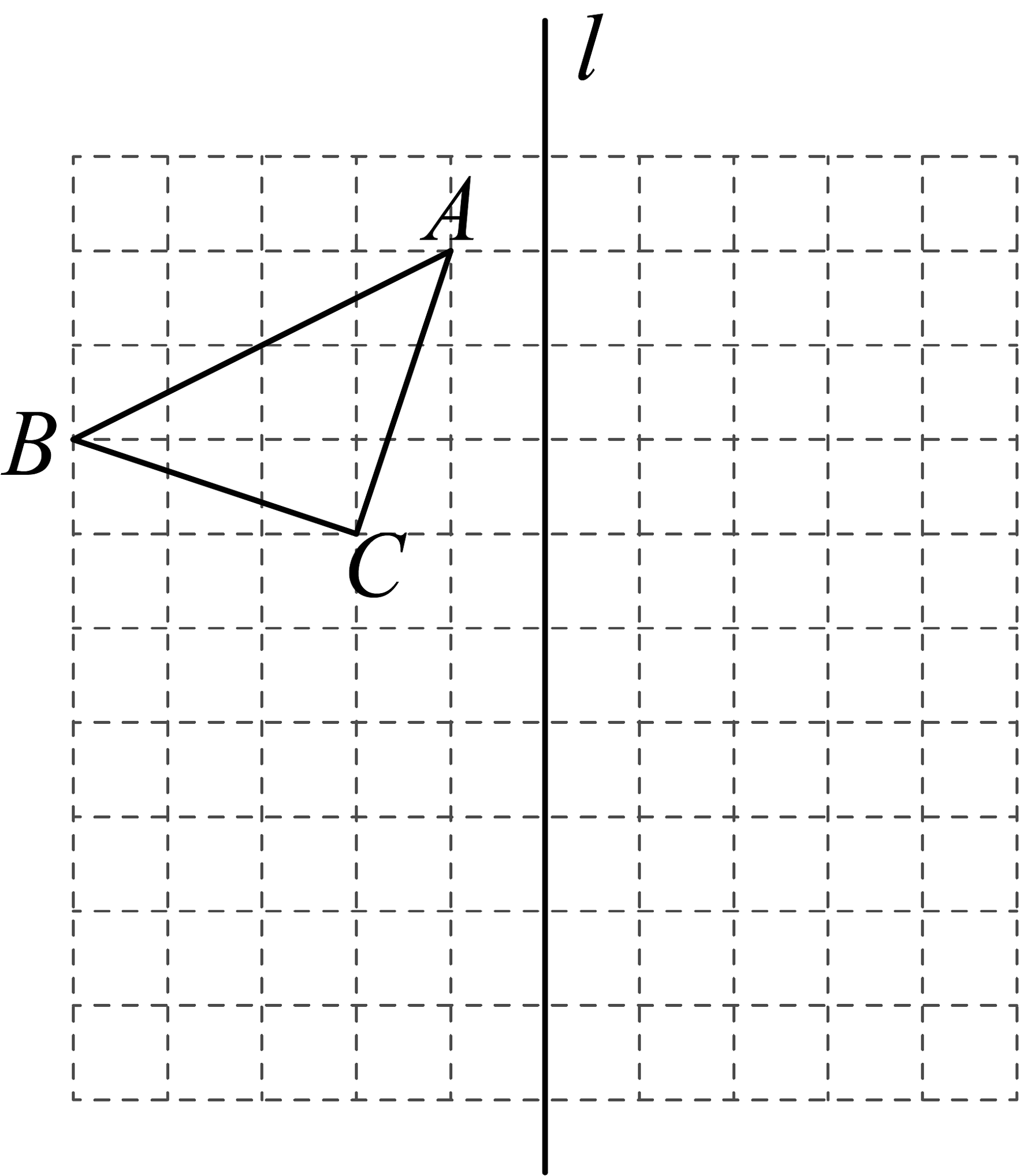 (1)、在网格中画出向下平移4个单位得到的再画出关于直线l对称的;(2)、求的面积.21. 手机给学生带来方便的同时也带来了很大的影响.某校七年级在一次家长会上对若干家长进行了一次对“学生使用手机”现象看法的调查,将调查数据整理得如下统计图(A:绝对弊大于利,B:绝对利大于弊,C:相对弊大于利,D:相对利大于弊):
(1)、在网格中画出向下平移4个单位得到的再画出关于直线l对称的;(2)、求的面积.21. 手机给学生带来方便的同时也带来了很大的影响.某校七年级在一次家长会上对若干家长进行了一次对“学生使用手机”现象看法的调查,将调查数据整理得如下统计图(A:绝对弊大于利,B:绝对利大于弊,C:相对弊大于利,D:相对利大于弊):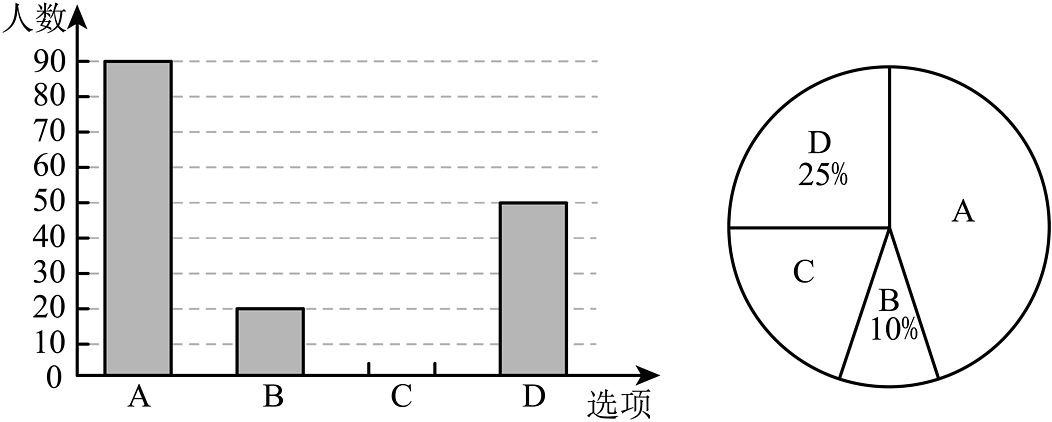 (1)、这次调查的家长总人数为多少人?(2)、本次调查的家长中表示“C:相对弊大于利”所占的百分比是多少?并补全条形统计图.(3)、求扇形统计图中表示“A:绝对弊大于利”的扇形的圆心角度数.22. 阅读理解——智慧数.
(1)、这次调查的家长总人数为多少人?(2)、本次调查的家长中表示“C:相对弊大于利”所占的百分比是多少?并补全条形统计图.(3)、求扇形统计图中表示“A:绝对弊大于利”的扇形的圆心角度数.22. 阅读理解——智慧数.定义:如果一个正整数能表示成两个正整数x,y的平方差,那么称这个正整数为“智慧数”.例如: , 所以16就是一个“智慧数”,我们可以利用进行研究.现给出下列结论:
①被4除余2的正整数都不是“智慧数”;
②除4以外所有能被4整除的正整数都是“智慧数”;
③所有的正奇数都是“智慧数”.
(1)、请判断7,24是否为“智慧数”,若是“智慧数”,请将7,24按“”照样写出:若不是“智慧数”,则不需写:(2)、题中给出的结论,其中正确的结论是;(填序号)(3)、把你认为是正确结论的进行说明理由.23. 综合与实践——折纸中的数学某兴趣小组在探究“过直线外一点作已知直线的平行线”的活动中,通过以下的折纸方式找符合要求的直线.如图1,在一张正方形纸片的两边上分别有A,B两点,连接是正方形纸片上一点,用折纸的方法过点P作的平行线的基本步骤如下.
第一步:如图2,过点P进行第一次折叠,使点B的对应点.B'落在上,折痕与互相垂直,垂足为Q,打开纸张铺平.
第二步:如图3,过点P进行第二次折叠,使折痕 , 打开纸张铺平(如图4).
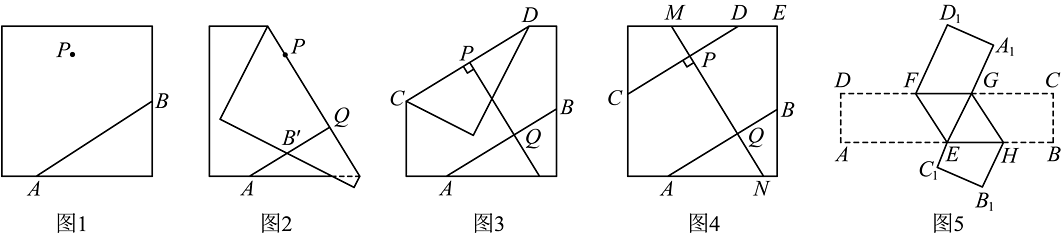
(1)根据上述步骤可知,与的位置关系是______.
【拓广】
(2)①如图4,设直线与正方形上、下两边分别交于点M,N,试探究与的数量关系,并说明理由:
②若 , 求的度数.
【迁移】
(3)如图5,在长方形纸片中, , 将纸片沿折叠,使落在处,再将纸片沿折叠,使落在处,且点 , 在同一直线上,求证: .