广东省江门市2024-2025学年八年级下学期数学期末试卷

试卷更新日期：2025-07-14 类型：期末考试

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分.在每个小题给出的四个选项中，只有一项符合题自要求.

1. 下列式子为最简二次根式的是（）

A、 $\sqrt{3}$ B、 $\sqrt{8}$ C、 $\sqrt{\frac{1}{m}}$ D、 $\sqrt{m^{2}}$

查看试题解析
2. $\sqrt{\frac{1}{3}} \times \sqrt{27}$ 的计算结果是（）

A、 $\pm 3$ B、3 C、 $\pm \sqrt{3}$ D、 $\sqrt{3}$

查看试题解析
3. 已知下列各三角形三边长，其中不能构成直角三角形的是（）

A、2，3，4 B、3，4，5 C、5，12，13 D、6，8，10

查看试题解析
4. 在△ABC中，AB=4，AC=3，BC=5，则∠ABC的面积是（）

A、4 B、5 C、6 D、7

查看试题解析
5. 在□ABCD中，对角线AC，BD相交于点O，AC=6，则OA的长度为（）

A、12 B、6 C、4 D、3

查看试题解析
6. 如图，这是不完整的推理过程，为保证推理成立，需在四边形ABCD中添加条件.下列对于嘉嘉和淇淇添加的条件的判断正确的是（）
嘉嘉：AD//BC.淇淇：AB=CD.
∵∠A+∠D=180°，
∴AB//CD.
∵____
∴四边形ABCD是平行四边形.

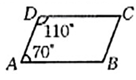A、只有嘉嘉的正确 B、只有洪淇的正确 C、两人的都正确 D、两人的都不正确

查看试题解析
7. 已知一次函数y-3x+1的图象向上平移t（↑>0）个单位长度后，其图象经过点（2，8），则t的值为（）

A、1 B、2 C、3 D、4

查看试题解析
8. 已知某植物园的成人票每张50元，学生票每张20元.设植物园已收门票的总费用为y元，若植物园内有成人x名和学生1名，则y与x之间的函数解析式为（）

A、y=20x B、y=50x C、y=20x+50 D、y=50x+20

查看试题解析
9. 如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4.D是边AB上的动点，过点D分别作边AC，BC的垂线DE，DF，垂足分别为E，F.连接EF，则EF的最小值为（）

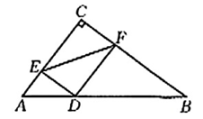A、3 B、2.4 C、4 D、2.5

查看试题解析
10. 某校为强化学生安全教育学习成果，考查学生面对突发事件的应急处理能力和自救互救能力，组织七、八年级学生进行了理论知识测试（分数为整数，满分为10分）.已知两个年级被随机抽取参与测试的学生人数相同，根据成绩整理并绘制了如图所示的统计表和统计图，下列判断正确的是（）
统计量
平均数
众数
中位数
方差
七年级
8
8
c
1.16
八年级
8
b
8
1.56

A、两个年级被抽取参与测试的学生人数均为40 B、若该校八年级有900名学生，估计该校八年级学生成绩为满分的人数约为105 C、b=9，c=8 D、七年级测试成绩为9分的学生人数最多，说明七年级学生成绩较稳定

查看试题解析

二、填空题:本大题共5小题，每小题3分，共15分.

11. 计算： $(\sqrt{3})^{2} =$ .

查看试题解析
12. 计算 $(2 \sqrt{48} - 3 \sqrt{27}) \div \sqrt{6}$ 的结果是.

查看试题解析
13. 当前，我国新能源汽车产业实现了快速发展，产销量和出口量均居世界第一，形成了完整且竞争力强的产业链，涌现了一批具有国际竞争力的企业，某汽车制造公司对旗下四款新型新能源汽车进行续航性能测试，下表记录了A，B，C，D四款车型在满电状态下的平均续航里程（单位：km）与续航里程的方差：
车型
A款
B款
C款
D款
均续航里程/km
420
420
410
400
方差
0.03
0.06
0.03
0.05
根据表中数据，要选择一款平均续航里程长且续航表现稳定的车型投人市场，应该选择款车型.

查看试题解析
14. DeepSeek训练AI模型时，GPU温度y（单位：℃）与运行时间x（单位：h）的关系如图所示，则运行到10h时，GPU的温度是℃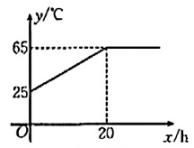

查看试题解析
15. 中国传统房屋往往将屋脊做成三角形形状，如图1，用三角形房梁支撑房擦，做成三角形屋脊，图2是房梁的平面图，MN是加固房梁的一根横撑.若AB=AC=5米，BC＝6米，M为BC的中点，MN⊥AC于点N.则MN的长度为米.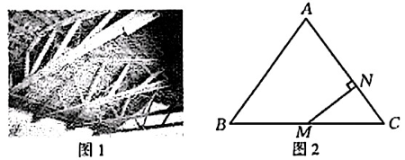

查看试题解析

三、解答题（一）:本大题共3小题，共21分，其中16题6分，17题7分，18题8分.

16. 计算：

(1)、 $4 \sqrt{12} - 6 \sqrt{\frac{1}{3}} + \sqrt{48}$ ；

(2)、 $(3 \sqrt{2} + 2 \sqrt{3}) (3 \sqrt{2} - 2 \sqrt{3})$ .

查看试题解析
17. 在数学课外学习活动中，小明和他的同学遇到一道题：
已知 $a = \frac{1}{2 + \sqrt{3}}$ ，求 $2 a^{2} - 8 a + 1$ 的值.
对于该题，小明是这样解答的：
∵ $a = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ，
∴ $a - 2 = - \sqrt{3}$ ，
∴ $(a - 2)^{2} = 3$ ， $a^{2} - 4 a + 4 = 3$ ，
∴ $a^{2} - 4 a = - 1$ ，
∴ $2 a^{2} - 8 a + 1 = 2 (a^{2} - 4 a) + 1 = 2 \times (- 1) + 1 = - 1$ .
请你根据小明的解题过程，解决以下问题：

(1)、 $\frac{1}{\sqrt{2} + 1} =$ ； $\frac{1}{\sqrt{3} + \sqrt{2}} =$

(2)、化简： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + ⋯ + \frac{1}{\sqrt{169} + \sqrt{168}}$ .

(3)、若 $a = \frac{1}{\sqrt{5} - 2}$ ，求 $a^{2} - 4 a + 3$ 的值.

查看试题解析
18. 为提高学生的劳动技能，某学校开辟了一块空地并在空地上搭建大棚，数学兴趣小组在空地上种下某速生植物的种子，种植后第5天种子开始发芽（记长度为0cm）.组员在每天同一时间对该速生植物的长度进行了测量并记录，第10天该速生植物的长度为20cm.经过研究，发现该速生植物的长度y（单位：cm）与种植时间x（单位：天）成一次函数关系.

(1)、请根据以上信息在所给的平面直角坐标系中画出函数图象．

(2)、求第20 天该植物的长度．

查看试题解析

四、解答题（二）:本大题共3小题，每小题9分，共27分.

19. 植树造林是生态文明建设的重要一环.2025年4月3日，习近平总书记在参加首都义务植树活动时强调绿化祖国必须坚持“三绿”并举、“四库”联动，要更加注重“提质”“兴业”“利民”.某校组织学生参加植树活动，要求每人植树4~7棵，活动结束后随机调查了部分学生植树的棵数，并将调查结果整理并绘制成如下不完整的统计图，
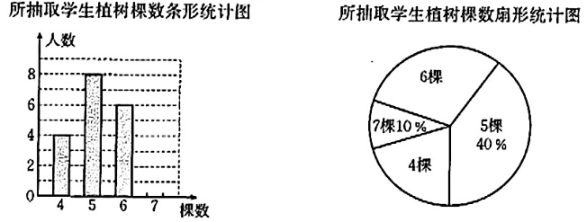
根据以上信息，解答下列问题：

(1)、补全条形统计图，所抽取学生植树棵数的中位数是棵，众数是棵.

(2)、求所抽取的学生平均每人植树的棵数.

(3)、若该校共有500名学生参加此次植树活动，请你估计该校此次活动植树的总棵数。

查看试题解析
20. 如图，在□ABCD中，BE⊥AD，交DA的延长线于点E，AE=AD.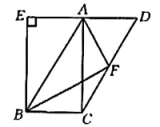

(1)、求证：四边形AEBC是矩形.

(2)、F为CD的中点，连接AF，BF.已知AB=6，BF⊥AF，求BF的长.

查看试题解析
21. 如图，直线 $l : y = \sqrt{3} x + \sqrt{3}$ 与x轴、y轴分别交于B，A两点，M为线段AB的中点.

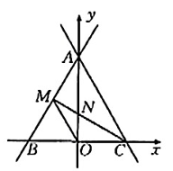(1)、求点A，B，M的坐标.

(2)、直线l关于y轴对称的直线为 $l^{^{'}}$ ，直线 $l^{^{'}}$ 交x轴于点C，求直线 $l^{^{'}}$ 的解析式.

(3)、在（2）的条件下，直线MC与y轴的交点为N，连接OM，求 $\frac{O M}{O N}$ 的值.

查看试题解析

五、解答题（三）:本大题共2小题，共27分，其中22题13分，23题14分.

22. 综合与实践
【项目背景】在数字化农业快速发展的时代，大数据分析与智能决策在水果产业中的作用愈发关键，芒果作为深受消费者喜爱的热带水果，其市场需求持续增长，为提升芒果产业的整体效益，实现精准化种植与科学化管理，某农业科技研究小组针对2024年n个芒果主产区的产量数据展开深入研究，通过对这些数据的专业分析，为芒果种植园的规划布局、采摘时间安排、仓储保鲜策略及市场销售渠道拓展提供有力的数据支撑，借助科技力量优化芒果产业的全产业链环节.
【数据收集与整理】将收集的n个芒果主产区的产量（产量记为x，单位：万吨）数据进行如下分组：
组别
A
B
C
D
E
x/万吨
30≤x<40
40≤x<50
50≤x<60
60≤x<70
70≤x<80
整理数据后得到部分信息如下：
①C组的数据（单位：万吨）为51，56，56，54，55，58.
②2024年芒果主产区产量的频数分布直方图和扇形统计图如图所示.
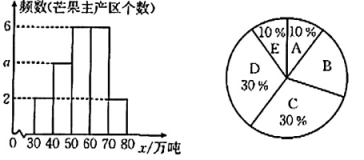
（任务1）n=    ▲         ， a=    ▲        .
【数据分析与运用】（任务2）C组数据的众数是    ▲        、收集的这n个芒果主产区2024年芒果产量的中位数是    ▲        .
（任务3）2024年各组芒果的平均产量如下表：
组别
A
B
C
D
E
平均产量/万吨
35
43
55
68
74
求这n个芒果主产区2024年芒果的平均产量.
（任务4）下列结论正确的是    ▲        （填序号）.
①如果收集的n个芒果主产区的产量数据都增加0.5万吨，那么这些地区芒果产量的总数
会增加0.5万吨.
②如果A组的所有数据都增加5万吨，那么这n个芒果主产区芒果产量的平均数会增加0.5万吨.
③如果各地区芒果产量数据的最大值与最小值相差40万吨，且最低产量在A组，那么最高产量一定在E组.

查看试题解析
23. 综合与探究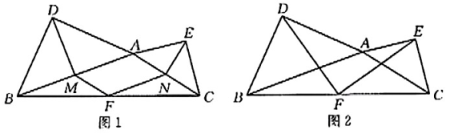
【问题情境】在△ABC中，分别以AB和AC为边向外作等腰直角三角形ABD和等腰直角三角形ACE，其中∠ADB=∠AEC=90°，AD=BD，AE=CE，F是边BC的中点.
【猜想验证】

(1)、如图1，若DM丄AB，ENLAC，垂足分别是M，N，连接MF，NF.试判断四边形AM-FN的形状，并说明理由。

(2)、【深入探究】
如图2，连接DF，EF.
①试判断线段DF与EF的数量关系和位置关系，并说明理由，
②若DF= $\sqrt{2}$ ，求四边形ADBC和△ACE的面积之和.

查看试题解析

统计量	平均数	众数	中位数	方差
七年级	8	8	c	1.16
八年级	8	b	8	1.56

车型	A款	B款	C款	D款
均续航里程/km	420	420	410	400
方差	0.03	0.06	0.03	0.05

组别	A	B	C	D	E
x/万吨	30≤x<40	40≤x<50	50≤x<60	60≤x<70	70≤x<80

组别	A	B	C	D	E
平均产量/万吨	35	43	55	68	74