广东省深圳市龙岗区2024-2025学年七年级下学期期末考试数学试题
试卷更新日期:2025-07-14 类型:期末考试
一、选择题(本大题共8小题,每小题3分,共24分,每小题有四个选项,其中只有一个是正确的)
-
1. 2024年12月4日,我国的传统节日“春节”被成功列入《人类非物质文化遗产代表作名录》。在春节期间贴窗花已经是一种历史悠久的习俗。下面几幅漂亮的窗花剪纸图案中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 某科技公司研发的智能系统在分析数据时,其算法对微观结构的测量精度可达0.00000009米,用科学记数法表示0.00000009=9×10n , 则n为( )A、-9 B、9 C、-8 D、83. 如图,要把河中的水引到水池A中,应在河岸B处(AB丄CD)开始挖渠才能使水渠的长度最短,这一做法蕴含的数学原理是( )
2. 某科技公司研发的智能系统在分析数据时,其算法对微观结构的测量精度可达0.00000009米,用科学记数法表示0.00000009=9×10n , 则n为( )A、-9 B、9 C、-8 D、83. 如图,要把河中的水引到水池A中,应在河岸B处(AB丄CD)开始挖渠才能使水渠的长度最短,这一做法蕴含的数学原理是( )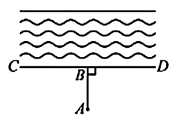 A、点到直线,垂线段最短 B、经过一点有无数条直线 C、两点确定一条直线 D、两点之间,线段最短4. 下列计算正确的是( )A、 B、 C、 D、5. 将一副三角板按不同位置摆放,下列选项中,∠α与<β互余的是( )A、
A、点到直线,垂线段最短 B、经过一点有无数条直线 C、两点确定一条直线 D、两点之间,线段最短4. 下列计算正确的是( )A、 B、 C、 D、5. 将一副三角板按不同位置摆放,下列选项中,∠α与<β互余的是( )A、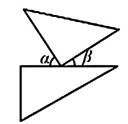 B、
B、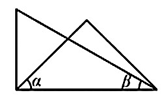 C、
C、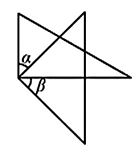 D、
D、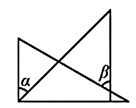 6. 数学兴趣小组做“抛瓶盖试验”获得的数据如下表:
6. 数学兴趣小组做“抛瓶盖试验”获得的数据如下表:拋掷次数
100
200
300
400
500
600
700
800
900
1000
盖口向上的频数
64
118
189
252
310
370
434
498
558
621
盖口向上的频率
0.64
0.59
0.63
0.63
0.62
0.61
0.62
0.62
0.62
0.62
下列说法正确的是( )
A、根据实验结果,“盖口向上”和“盖口向下”具有等可能性 B、若再抛掷瓶盖100次,则一定有62次“盖口向上” C、若抛掷瓶盖10次,结果“盖口向上”8次,则“盖口向上”的概率为0.8 D、若抛掷瓶盖2000次,则“盖口向上”的次数大约有1240次7. 如图,点E在BC的延长线上,下列条件能判定ABI//CD的是( )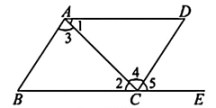 A、∠1=∠2 B、∠D=∠5 C、∠3=∠4 D、∠1+∠3+∠B=180°8. 漏刻是我国古代的一种计时工具,据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用。数学活动小组依据漏刻的原理制作了一个简单的漏刻计时工具模型,每2分钟记录一次箭尺读数,得到漏刻水位h(cm)与时间t(min)的实验数据如下表:
A、∠1=∠2 B、∠D=∠5 C、∠3=∠4 D、∠1+∠3+∠B=180°8. 漏刻是我国古代的一种计时工具,据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用。数学活动小组依据漏刻的原理制作了一个简单的漏刻计时工具模型,每2分钟记录一次箭尺读数,得到漏刻水位h(cm)与时间t(min)的实验数据如下表:数据记录
第1次
第2次
第3次
第4次
第5次
……
t(min)
0
2
4
6
8
……
h(cm)
2
2.8
3.6
4.2
5.2
……
下列说法错误的是( )
A、在实验开始时,漏刻水位是2cm B、第4次数据记录出现了错误,正确的漏刻水位应该是4.4cm C、第7次数据记录时,漏刻水位应为6.8cm D、当漏刻水位为10cm时,对应实验的时间是10min二、填空题(本大题共5小题,每小题3分,共15分)
-
9. 已知一个三角形的边长均为整数,且其中两条边长分别3cm和5cm,则第三边的长度可能是cm。(写出满足条件的一个答案即可)10. 如图,左图是一个可调节平板支架,其结构示意图如右图所示,当CB平分∠ACD时,点B到桌面CD的距离是12cm,则点B到AC的距离是cm。
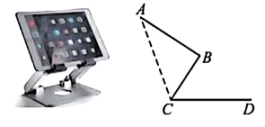 11. 如图是某款婴儿手推车的平面示意图,若∠1=130°,∠2=85°,则∠3的度数为。
11. 如图是某款婴儿手推车的平面示意图,若∠1=130°,∠2=85°,则∠3的度数为。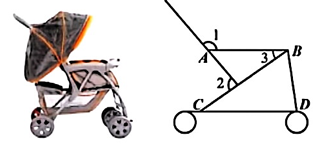 12. 如图,秋千OB垂直地面时所在直线与地面交于点E,当秋千拉至OA处,点A距离地面高度AD=0.7m,与OB的水平距离DE=1.2m。推动秋千从OA至OC处,此时恰好∠AOC=90°,点C距离OB的水平距离EF=2m,则点C距离地面的高度CF为m。
12. 如图,秋千OB垂直地面时所在直线与地面交于点E,当秋千拉至OA处,点A距离地面高度AD=0.7m,与OB的水平距离DE=1.2m。推动秋千从OA至OC处,此时恰好∠AOC=90°,点C距离OB的水平距离EF=2m,则点C距离地面的高度CF为m。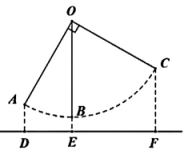 13. 如图,正方形ABCD和正方形AEFG的面积和为15,D、A、E三点共线且DE=5,则图中阴影部分图形的面积为。
13. 如图,正方形ABCD和正方形AEFG的面积和为15,D、A、E三点共线且DE=5,则图中阴影部分图形的面积为。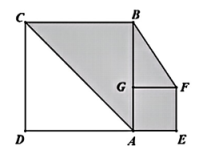
三、解答题(本题共7小题,共61分)
-
14. 计算:(1)、(2)、15. 先化简,再求值: , 其中。16. 某学校班级为表彰一周量化考核评价为优秀的同学,设制如图1的电子刮刮卡抽奖活动,评为优秀的同学获得抽奖机会一次。其中4张刮刮卡奖励内容分别为“①免作业券1张;②与好朋友同桌一天:③薯片一包;④牛奶1瓶”。抽完奖后系统自动更新出4张上述内容的刮刮卡,并把顺序打乱。
 (1)、小明同学在某周考核中评为优秀,他在刮刮卡抽奖活动中抽中“①”的概率是:(2)、通过调查发现,该班同学对“①”最感兴趣,对“③”和“④”喜好程度一样。于是,老师将抽奖方式改为转盘,并设定:①的概率是 , ②的概率是 , ③的概率为。请在图2转盘中的扇形写上“①②③④”,使得自由转动这个转盘,当它停止时,指针分别落在“①②③④”上的概率满足上述设定。(备注:转盘中扇形的圆心角均相等)17. 小亮骑自行车去上学,当他以往常的速度骑行至点A处时,忽然想起要买某本书,于是又折回到刚经过的一家书店,买到书后继续赶去学校。以下是他本次上学离家距离与时间的关系示意图。根据图中提供的信息回答下列问题:
(1)、小明同学在某周考核中评为优秀,他在刮刮卡抽奖活动中抽中“①”的概率是:(2)、通过调查发现,该班同学对“①”最感兴趣,对“③”和“④”喜好程度一样。于是,老师将抽奖方式改为转盘,并设定:①的概率是 , ②的概率是 , ③的概率为。请在图2转盘中的扇形写上“①②③④”,使得自由转动这个转盘,当它停止时,指针分别落在“①②③④”上的概率满足上述设定。(备注:转盘中扇形的圆心角均相等)17. 小亮骑自行车去上学,当他以往常的速度骑行至点A处时,忽然想起要买某本书,于是又折回到刚经过的一家书店,买到书后继续赶去学校。以下是他本次上学离家距离与时间的关系示意图。根据图中提供的信息回答下列问题: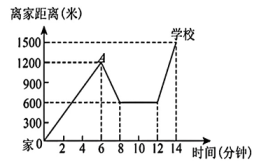 (1)、图象所表示的两个变量中,自变量是;因变量是:(2)、小亮家到学校的距离是米;本次上学途中,小亮一共骑行了米;(3)、点A的实际意义是什么?(4)、如果小亮不买书,以往常的速度去学校,从家到学校需要多少分钟?18. 【课本回顾】你还记得怎样用尺规作一个角等于已知角吗?你能说明其中的道理吗?小明回顾了作图过程,并进行了如下思考:
(1)、图象所表示的两个变量中,自变量是;因变量是:(2)、小亮家到学校的距离是米;本次上学途中,小亮一共骑行了米;(3)、点A的实际意义是什么?(4)、如果小亮不买书,以往常的速度去学校,从家到学校需要多少分钟?18. 【课本回顾】你还记得怎样用尺规作一个角等于已知角吗?你能说明其中的道理吗?小明回顾了作图过程,并进行了如下思考: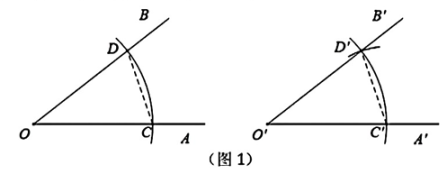
如图1,由尺规作图可知,OC=O'C',OD=O'D', ①
所以△OCD≌△O'C'D'( ② ),(填全等判定依据,如SSS,ASA,AAS,SAS)
(1)、完成上述小明思考过程中的填空;(2)、【操作应用】如图2,已知线段a和∠α,请用尺规作一个△ABC,使BC=a,AC=2a,∠BCA=∠α;
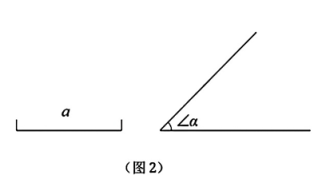 (3)、如图3,在四边形ABCD中,AB=AD,请利用尺规在CD边上作一点E,使得△ADE≌△ABE。(保留作图痕迹,标明字母,不写作法)
(3)、如图3,在四边形ABCD中,AB=AD,请利用尺规在CD边上作一点E,使得△ADE≌△ABE。(保留作图痕迹,标明字母,不写作法)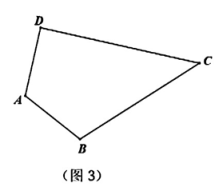 19.(1)、【特例感知】
19.(1)、【特例感知】已知:152=225,252=625,352=1225,·……
猜想:个位数字是5的两位数平方后,结果末尾的两个数字是25。
证明:设此两位数的十位数字是m,……
请完成上述剩余证明过程。
(2)、【类比迁移】观察下列等式:
32×38=1216;54×56=3024;79×71=5609;83×87= ▲ ;
①请写第四个等式的结果;
②数学兴趣小组发现,这若干组等式满足下列的规律:
十位数字相同、个位数字之和等于10的两个两位数相乘,可以把十位数字乘比它大1的数作为积的前两位,把个位数字的乘积作为积的后两位。”
例如
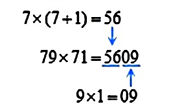
请写出一个满足此规律的一个等式: ▲ ;(不得抄写已给出的4个等式)
③设满足此规律的两个两位数中十位数字为a,其中第一个两位数的个位数字为b。请用含a、b的式子表示②中的规律,并证明其正确性。
20. 【背景】数学兴趣小组在学习对顶角知识时,发现若两个三角形存在对顶角的关系时,则这两个三角形的内角存在某种关系,对此数学兴趣小组展开探究。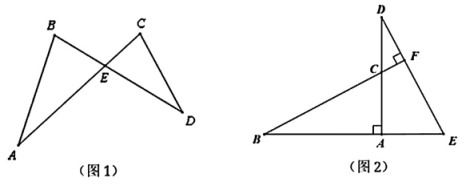 (1)、【发现】如图1,在△ABE和△DCE中,点E为AC与BD的交点。
(1)、【发现】如图1,在△ABE和△DCE中,点E为AC与BD的交点。①若∠A+∠B=100°,则∠C+∠D=;
②若∠B=∠C,则∠A与∠D之间的数量关系是;
(2)、【应用】如图2,B、A、E在同一直线上,DA⊥BE,BF⊥DE交AD于点C,BC=DE。求证:△ABC≌△ADE;
(3)、如图3,在等腰△ABC中,AB=AC,∠B=30°,D是BC边上一点,将△ABD沿AD折叠至△ADE,AB的对应边AE与BC交于点F,当△ADF为等腰三角形时,直接写出∠CDE的度数: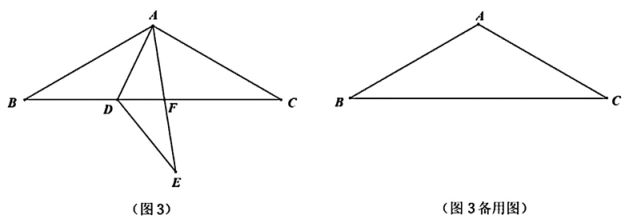 (4)、如图4,在Rt△ABC中,∠ABC=90°,BD是AC边上的高,AD=2,E是∠ABC外一点且满足∠EDC=∠EBC,BA=BE,DE=BD。记BD =x,y=S△ABD-S△BDE , 求y与x的关系式。
(4)、如图4,在Rt△ABC中,∠ABC=90°,BD是AC边上的高,AD=2,E是∠ABC外一点且满足∠EDC=∠EBC,BA=BE,DE=BD。记BD =x,y=S△ABD-S△BDE , 求y与x的关系式。