广东省广州市番禺区2024-2025学年高一下学期期末教学质量监测数学试卷
试卷更新日期:2025-07-06 类型:期末考试
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 设集合 , , 则集合的元素个数为A、4 B、3 C、2 D、12. 已知复数 , , 在复平面内,复数和所对应的两点之间的距离是( )A、 B、10 C、 D、53. 如图,圆台的侧面展开图扇环的圆心角为 , 其中 , 则该圆台的高为( )
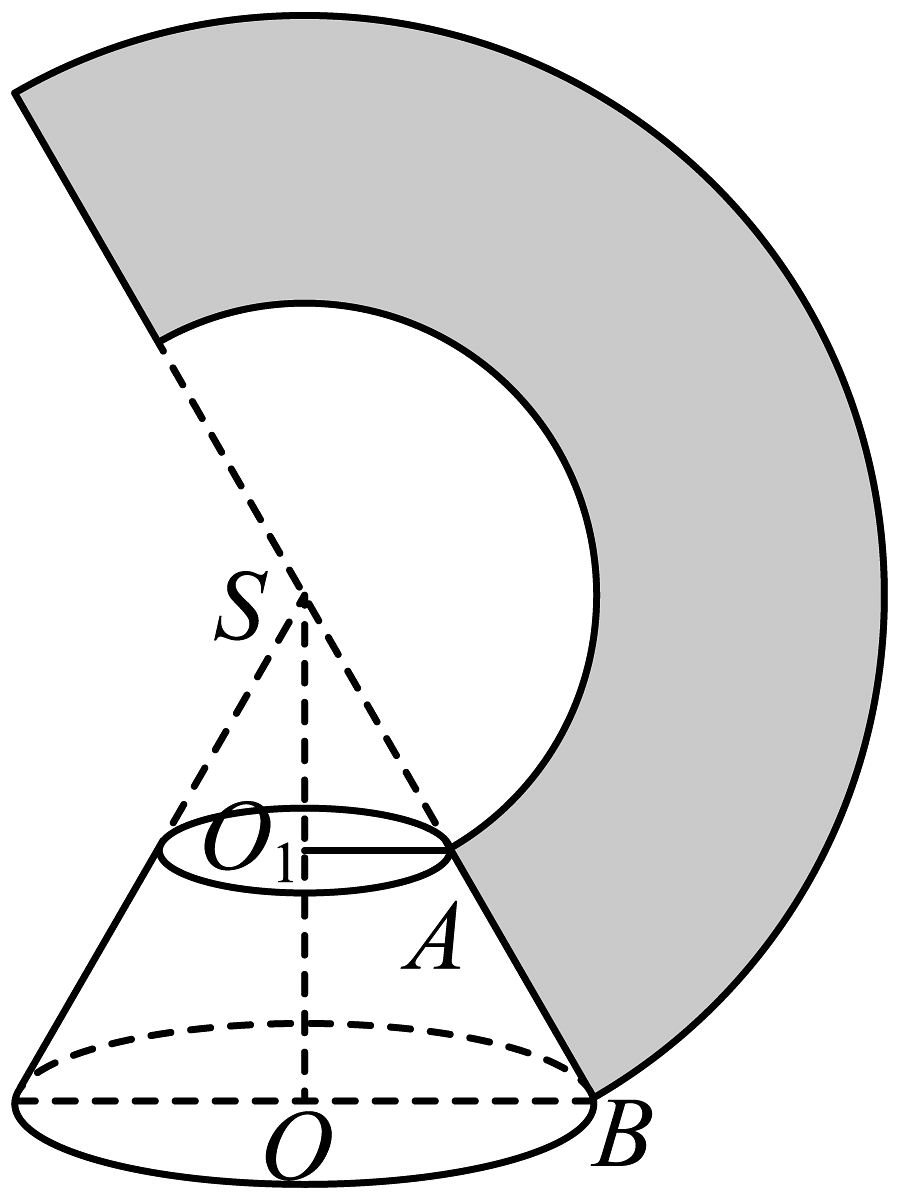 A、 B、 C、1 D、44. 已知 , , 则( )A、 B、 C、 D、或5. 已知一组数据39,41,44,46,49,50,x,55的第65百分位数是50,那么实数的取值范围是( )A、 B、 C、 D、6. 已知向量 , , 若 , 则实数( )A、3 B、6 C、 D、7. 已知函数 , 若 , 则的取值范围是( )A、 B、 C、 D、8. 对于一个古典概型的样本空间和事件A,B,C,D,用表示事件中的样本点个数.若 , , , , , , , , 则( )A、与对立 B、与不对立 C、与互斥 D、与相互独立
A、 B、 C、1 D、44. 已知 , , 则( )A、 B、 C、 D、或5. 已知一组数据39,41,44,46,49,50,x,55的第65百分位数是50,那么实数的取值范围是( )A、 B、 C、 D、6. 已知向量 , , 若 , 则实数( )A、3 B、6 C、 D、7. 已知函数 , 若 , 则的取值范围是( )A、 B、 C、 D、8. 对于一个古典概型的样本空间和事件A,B,C,D,用表示事件中的样本点个数.若 , , , , , , , , 则( )A、与对立 B、与不对立 C、与互斥 D、与相互独立二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
-
9. 如图,在长方体中, , 分别为 , 的中点, , 分别为 , 的中点,则下列说法正确的是( )
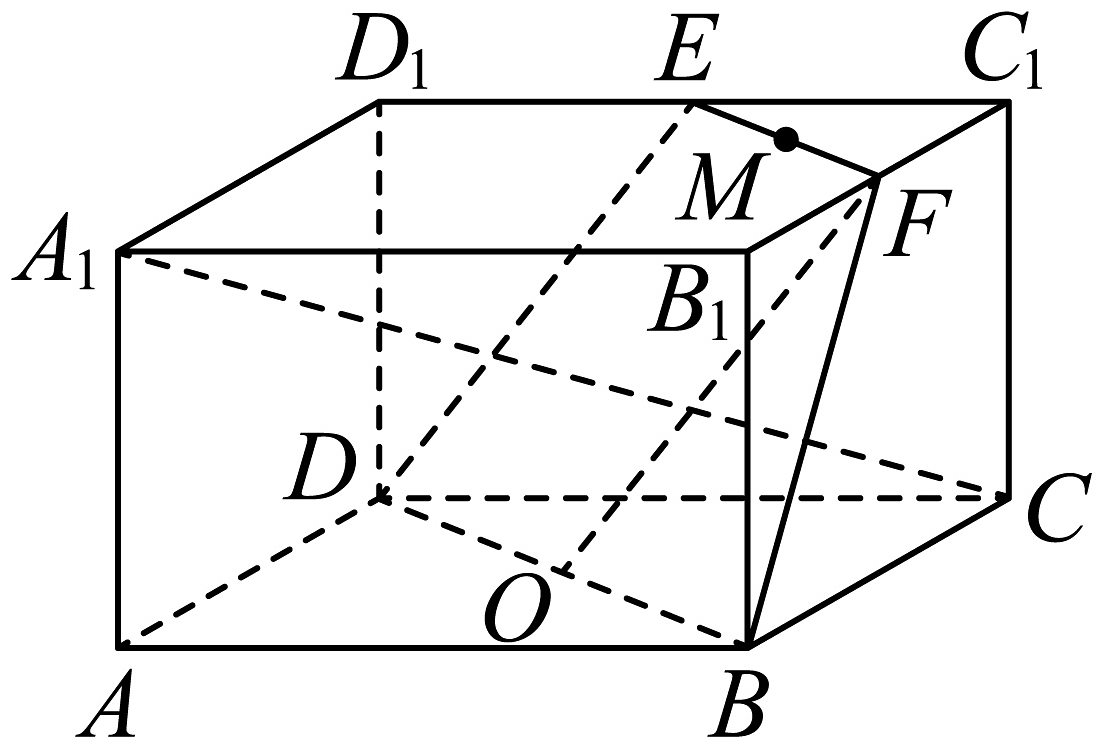 A、四点 , , , 在同一平面内 B、三条直线 , , 有公共点 C、直线与直线不是异面直线 D、直线上存在点使 , , 三点共线10. 假设某人在出生起180天内的体力、情绪、智力呈周期性变化,它们的变化规律遵循如图所示的正弦型曲线模型:
A、四点 , , , 在同一平面内 B、三条直线 , , 有公共点 C、直线与直线不是异面直线 D、直线上存在点使 , , 三点共线10. 假设某人在出生起180天内的体力、情绪、智力呈周期性变化,它们的变化规律遵循如图所示的正弦型曲线模型: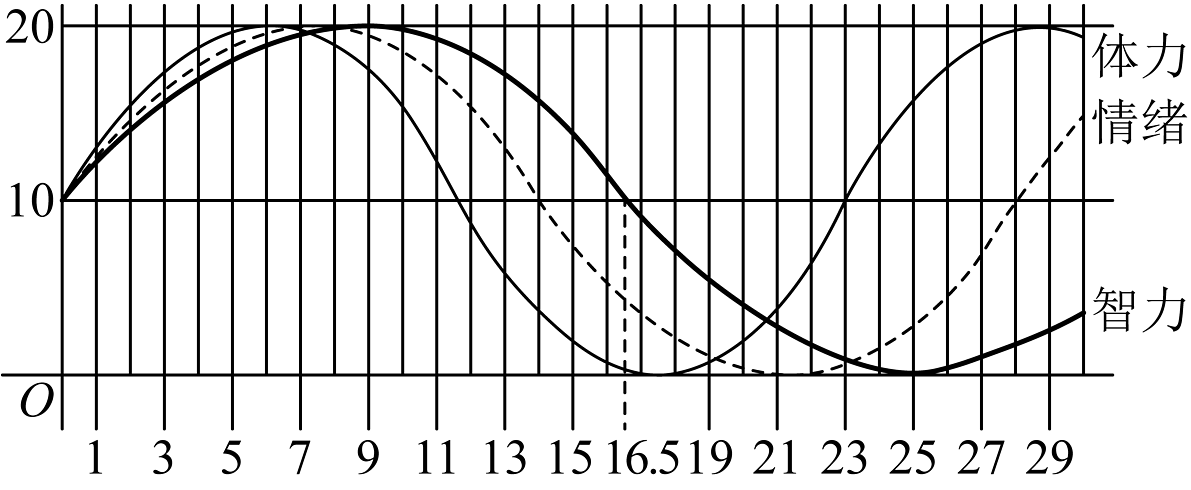
记智力曲线为 , 情绪曲线为 , 体力曲线为 , 且三条曲线的起点位于坐标系的同一点处、均为可向右延伸,则( )
A、智力曲线的最小正周期是三个曲线中最大的 B、在出生起180天内,体力共有7次达高峰值 C、第94天时,情绪值小于15 D、第62天时,智力曲线和情绪曲线均处于上升期11. 著名数学家狄利克雷在数学领域成就显著,以其命名的函数 , 被称为狄利克雷函数,其中为实数集,为有理数集,下面关于狄利克雷函数的正确结论是( )A、对于任意的 , 都有 B、函数是偶函数 C、若且为有理数,则对任意的恒成立 D、在图象上存在不同的三个点 , 使得为直角三角形三、填空题:本题共3小题,每小题5分,共15分.
-
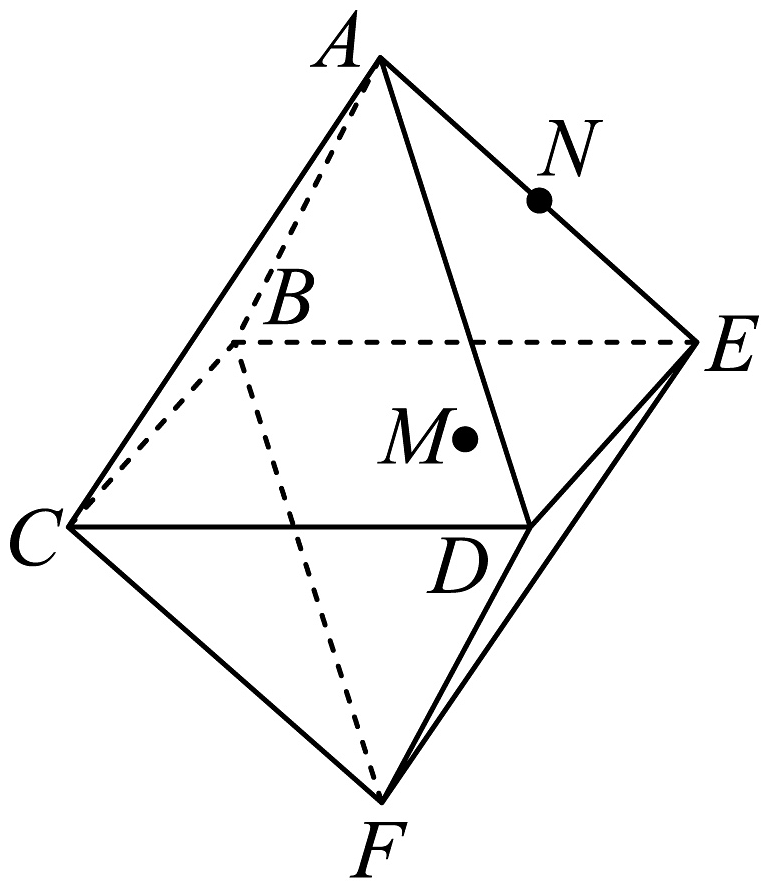
12. 使成立的一个充分而非必要的条件是 .13. 当时,的解集为 .14. 如图,八面体的每一个面都是边长为4的正三角形,且顶点B,C,D,E,在同一个平面内.若点在四边形内(包含边界)运动,当时,则点的轨迹的长度为 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
-
15. 如图,在四边形中, , , 设 , .
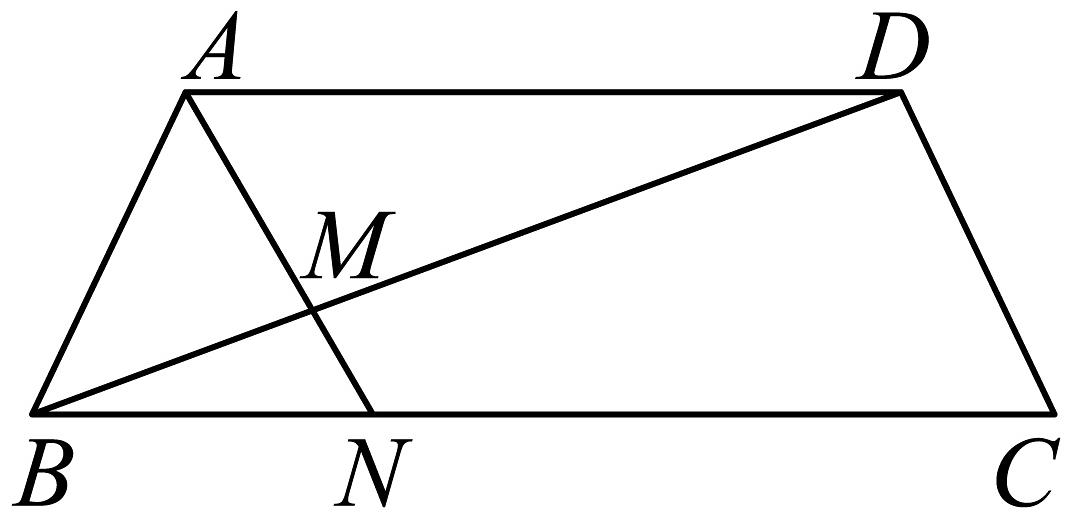 (1)、用 , 表示 , ;(2)、若与相交于点 , , , , 求 .16. 如图,已知三棱台中,平面平面、是以为直角顶点的等腰直角三角形,且 , .
(1)、用 , 表示 , ;(2)、若与相交于点 , , , , 求 .16. 如图,已知三棱台中,平面平面、是以为直角顶点的等腰直角三角形,且 , .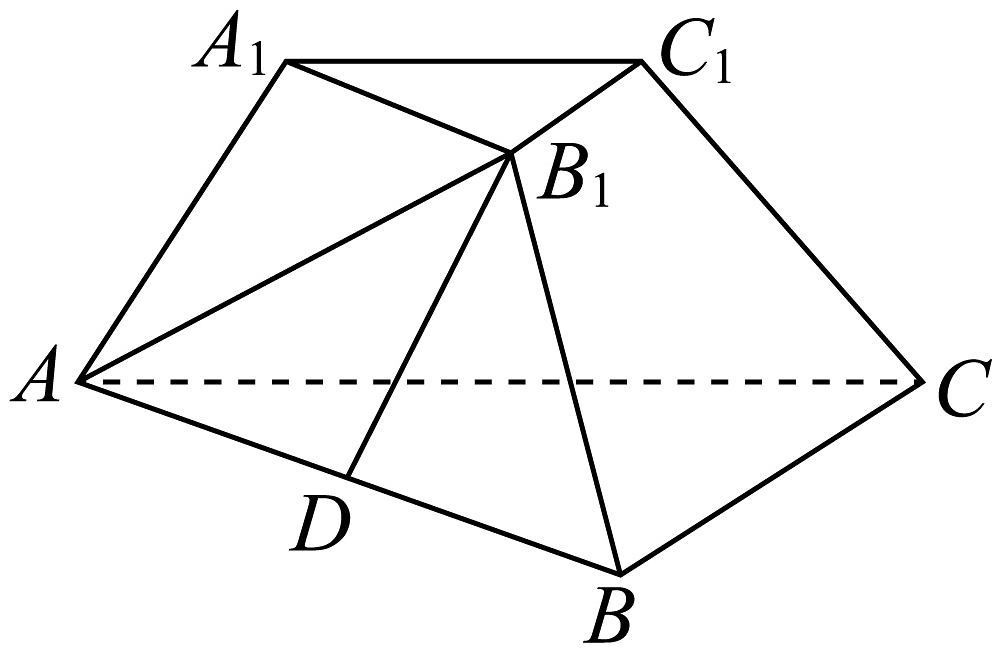 (1)、证明:平面;(2)、若的中点为 , 求直线与平面所成角的大小.17. 在花市志愿者选拔的面试结果中,随机抽取了100名候选者的面试成绩,并分成五组:第一组 , 第二组 , 第三组 , 第四组 , 第五组 , 绘制成如图所示的频率分布直方图.
(1)、证明:平面;(2)、若的中点为 , 求直线与平面所成角的大小.17. 在花市志愿者选拔的面试结果中,随机抽取了100名候选者的面试成绩,并分成五组:第一组 , 第二组 , 第三组 , 第四组 , 第五组 , 绘制成如图所示的频率分布直方图.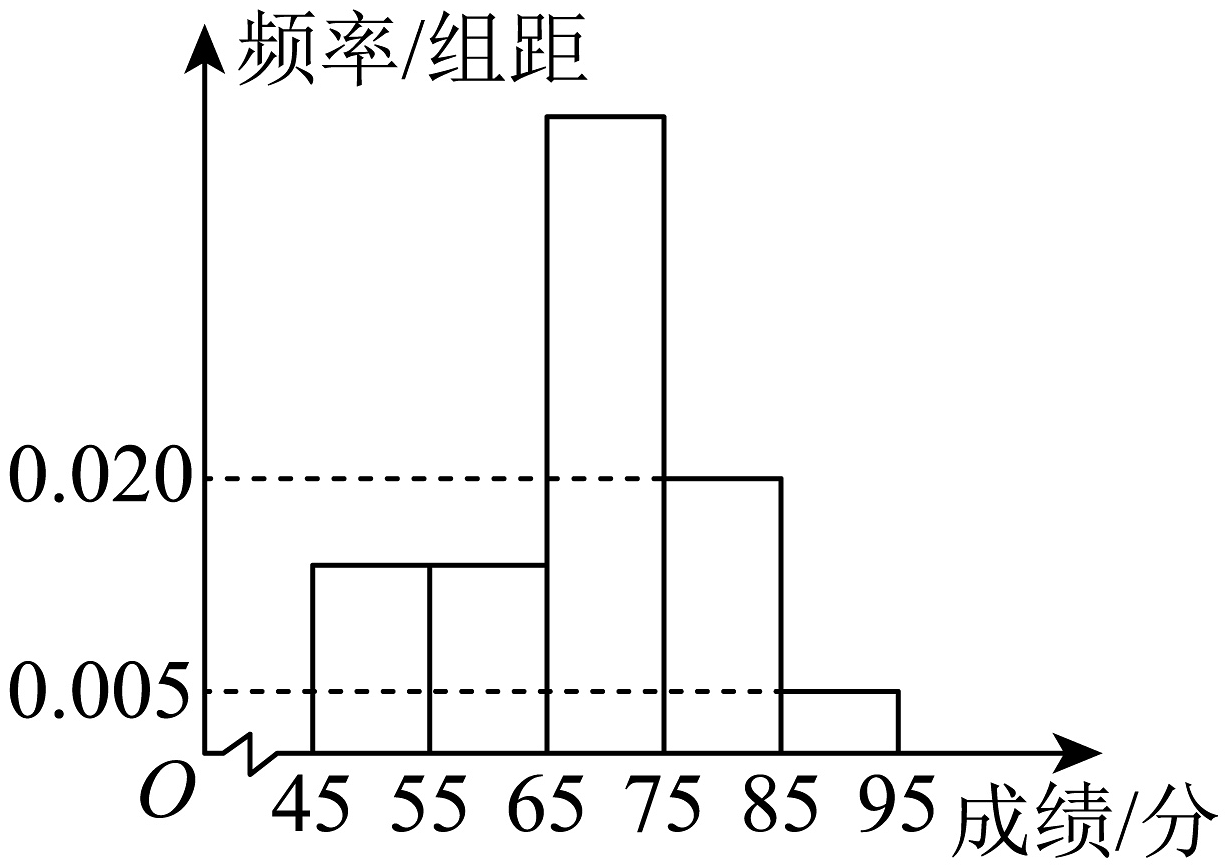 (1)、已知在上述分组中用分层随机抽样的方法从第四组和第五组中共选取了5人,若从这5人中用简单随机抽样的方法选取2人,求这两名候选者来自不同组的概率;(2)、若前三组候选者的面试成绩的平均数和方差分别为64和64,后两组候选者的面试成绩的平均数和方差分别为82和16,根据上述信息估计此次选拔所有候选者的面试成绩的平均数和方差.
(1)、已知在上述分组中用分层随机抽样的方法从第四组和第五组中共选取了5人,若从这5人中用简单随机抽样的方法选取2人,求这两名候选者来自不同组的概率;(2)、若前三组候选者的面试成绩的平均数和方差分别为64和64,后两组候选者的面试成绩的平均数和方差分别为82和16,根据上述信息估计此次选拔所有候选者的面试成绩的平均数和方差.