广东省佛山市顺德区普通高中2025届高三下学期5月适应性考试数学试题
试卷更新日期:2025-06-11 类型:高考模拟
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
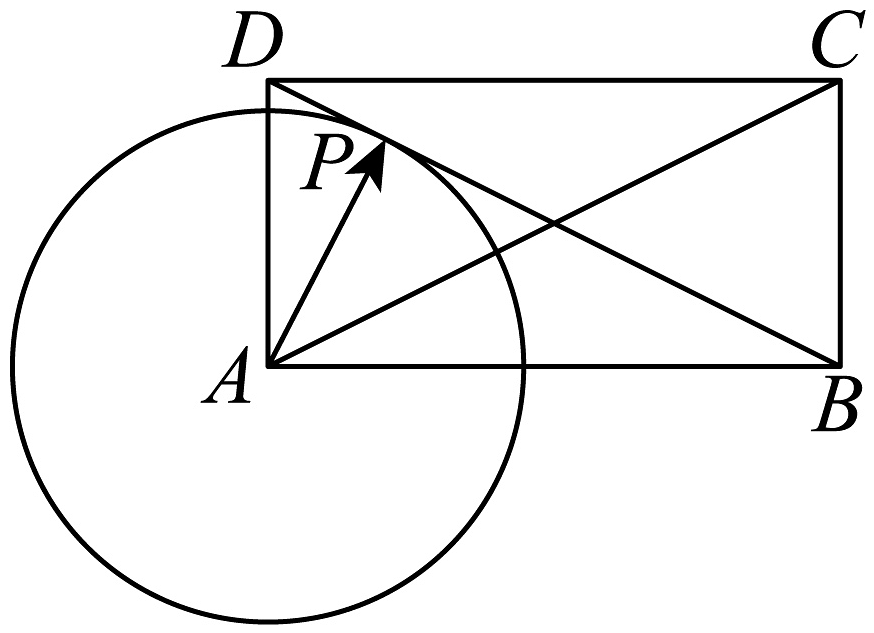
1. 复平面上两点对应的复数分别是 , 向量对应的复数为 , 则( )A、17 B、 C、13 D、2. 设集合 , 则的元素个数为( )A、6 B、5 C、4 D、33. 已知抛物线上的点的横坐标为4,抛物线的焦点为 . 若 , 则的值为( )A、18 B、9 C、4 D、24. 将函数的图象向右平移个单位长度,得到函数的图象,则下列结论正确的是( )A、是奇函数 B、的图象关于直线对称 C、在上的值域为 D、在上单调递增5. 若的展开式中的常数项为31,则( )A、 B、0 C、1 D、26. 如图,已知矩形的边长满足 , 以为圆心的圆与相切于 , 则( )
 A、 B、 C、8 D、7. 在中,角的对边分别为 . 已知 , 且的内角平分线 , 则面积的最小值为( )A、2 B、 C、3 D、8. 已知函数 , 若存在最小值,则实数的取值范围是( )A、 B、 C、 D、
A、 B、 C、8 D、7. 在中,角的对边分别为 . 已知 , 且的内角平分线 , 则面积的最小值为( )A、2 B、 C、3 D、8. 已知函数 , 若存在最小值,则实数的取值范围是( )A、 B、 C、 D、二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
-
9. 生活经验告诉我们,儿子的身高与父亲的身高不仅线性相关,而且还是正相关.有人调查了10名男大学生的身高(单位:)及其父亲身高(单位:)的数据 , 已知其中一组数据为 , 且 , 求得经验回归方程为 , 并绘制了如下残差图(残差观测值预测值),则
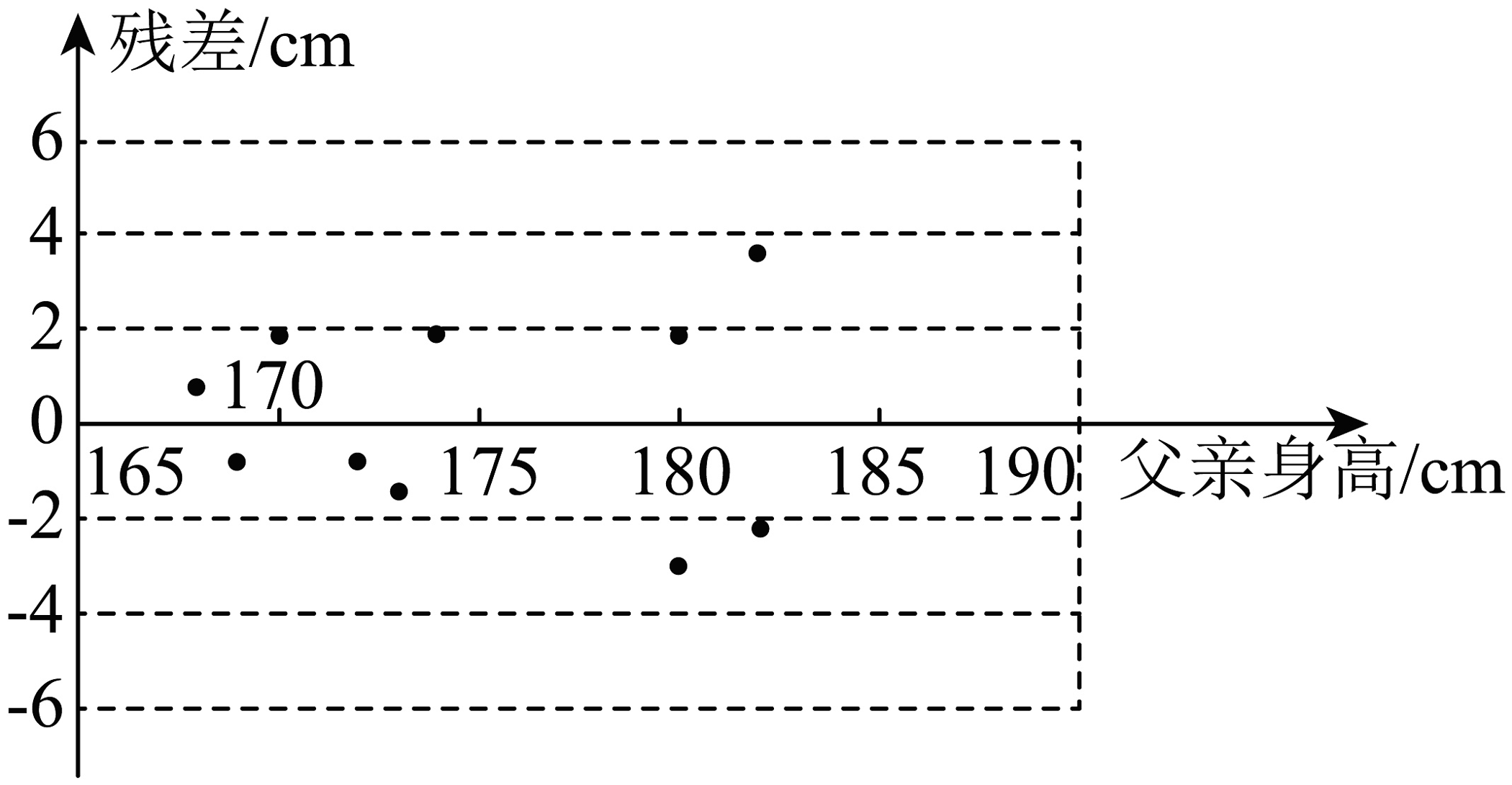 A、这10名男大学生的身高的平均值为176.75 B、由残差图可判定儿子身高与父亲身高的关系不符合上述回归模型 C、数据对应的残差为3.7 D、去掉数据后,重新求得的回归直线的决定系数变小10. 如图,已知棱长为2的正方体中心为 , 将四棱锥绕直线顺时针旋转之后,得到新的四棱锥 , 则( )
A、这10名男大学生的身高的平均值为176.75 B、由残差图可判定儿子身高与父亲身高的关系不符合上述回归模型 C、数据对应的残差为3.7 D、去掉数据后,重新求得的回归直线的决定系数变小10. 如图,已知棱长为2的正方体中心为 , 将四棱锥绕直线顺时针旋转之后,得到新的四棱锥 , 则( )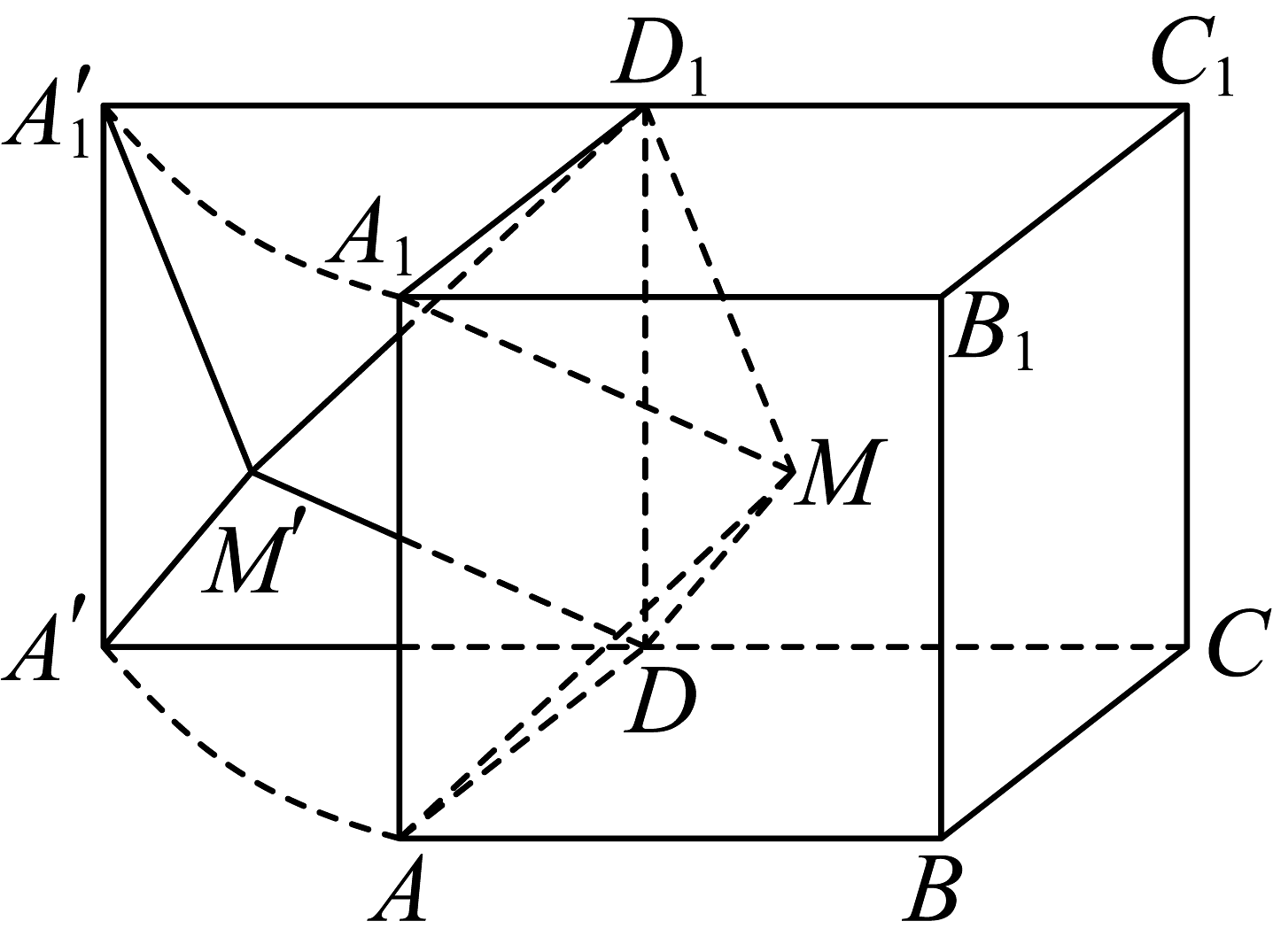 A、 B、当时,四棱锥顶点运动的轨迹长度为 C、当时,平面平面 D、存在旋转的角度 , 使得四点共面11. 已知函数及其导函数的定义域为 , 若为奇函数, , 且对任意 , , 则下列结论正确的是( )A、 B、 C、 D、
A、 B、当时,四棱锥顶点运动的轨迹长度为 C、当时,平面平面 D、存在旋转的角度 , 使得四点共面11. 已知函数及其导函数的定义域为 , 若为奇函数, , 且对任意 , , 则下列结论正确的是( )A、 B、 C、 D、三、填空题:本题共3小题,每小题5分(第14题第一空2分,第二空3分),共15分.
-
12. 已知函数 , 则 .13. 圆锥曲线在物理光学上都有各自光学性质.在双曲线中,从一个焦点发出的光线,经双曲线反射后,反射光线会散开,但反射光线的反向延长线经过双曲线的另一个焦点.已知双曲线的方程为 , 一束光线从的右焦点射出.经过反射后到达点 . 则光线从到所经过的路径长为 .14. 有个大小外观一致、重量各不相同的小纸箱和一个天平,设为确保找到第二重的小纸箱时使用天平的最少次数.则; .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
-
15. 已知数列满足 , 且是关于的方程的两个根.(1)、求;(2)、设 , 求数列的前21项和 .16. 已知函数 .(1)、若曲线在点处的切线经过坐标原点,求的值;(2)、若存在两个极值点,求的取值范围.17. 设椭圆的左、右焦点分别为 . 已知在椭圆上,且的面积为 .
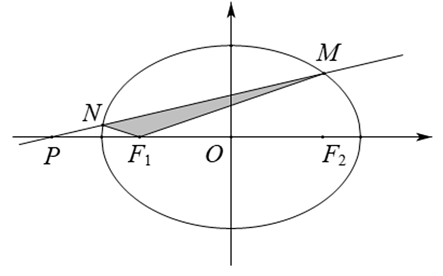 (1)、求椭圆的标准方程;(2)、如图,过点的直线与椭圆交于另一点与轴交于点 , 若 , 求的面积.18. 如图,在直三棱柱中, , . 侧棱 . 分别为上的动点,当运动到的中点时,异面直线与所成角的余弦值为 .
(1)、求椭圆的标准方程;(2)、如图,过点的直线与椭圆交于另一点与轴交于点 , 若 , 求的面积.18. 如图,在直三棱柱中, , . 侧棱 . 分别为上的动点,当运动到的中点时,异面直线与所成角的余弦值为 .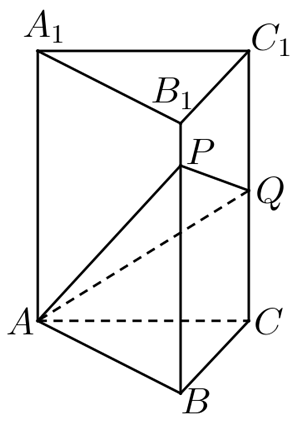 (1)、证明:是正三棱柱;(2)、若运动时,总满足 . 当面积最小时,求二面角的大小.19. 如图,四人围成一圈玩成语接龙游戏,游戏开始时随机抽取一个成语,第1次由接龙,下一次接龙的人由掷硬币决定,规则如下:随机掷3枚硬币,如果3枚硬币都是反面朝上,则第2次由接龙;如果3枚硬币中仅有1枚正面朝上,则第2次由接龙;如果3枚硬币中仅有2枚正面朝上,则第2次由接龙;如果3枚硬币都是正面朝上,则第2次由接龙.记第2次接龙的人(为或或或),再次掷3枚硬币决定下一次的接龙人,若掷出的硬币中有枚硬币正面朝上,则按顺时针方向数,下一次由后面的第个人接龙(若 , 则下一次由接龙).此后每次接龙以此类推.
(1)、证明:是正三棱柱;(2)、若运动时,总满足 . 当面积最小时,求二面角的大小.19. 如图,四人围成一圈玩成语接龙游戏,游戏开始时随机抽取一个成语,第1次由接龙,下一次接龙的人由掷硬币决定,规则如下:随机掷3枚硬币,如果3枚硬币都是反面朝上,则第2次由接龙;如果3枚硬币中仅有1枚正面朝上,则第2次由接龙;如果3枚硬币中仅有2枚正面朝上,则第2次由接龙;如果3枚硬币都是正面朝上,则第2次由接龙.记第2次接龙的人(为或或或),再次掷3枚硬币决定下一次的接龙人,若掷出的硬币中有枚硬币正面朝上,则按顺时针方向数,下一次由后面的第个人接龙(若 , 则下一次由接龙).此后每次接龙以此类推.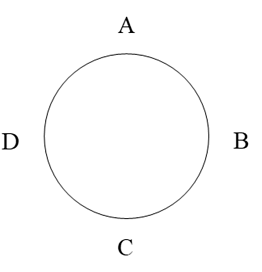 (1)、分别求出第2次由接龙的概率;(2)、记前3次中由接龙的次数为 , 求的分布列及期望;(3)、记第次由接龙的概率为 , 证明 .
(1)、分别求出第2次由接龙的概率;(2)、记前3次中由接龙的次数为 , 求的分布列及期望;(3)、记第次由接龙的概率为 , 证明 .