广东省深圳市福田区2024-2025学年八年级下学期数学期末教学质量检测

试卷更新日期：2025-07-11 类型：期末考试

进入出卷网下载

一、选择题(本题共8小题，每小题3分，共24分.每小题给出4个选项，其中只有一个是正确的.)

1. 下列由 AI 设计的四组图案中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知 $x < y$ ，则下列不等式一定成立的是（）

A、 $x + 1 > y + 1$ B、 $- 2 x < - 2 y$ C、 $x - 2 > y - 2$ D、 $\frac{x}{2} < \frac{y}{2}$

查看试题解析
3. 下列分式是最简分式的是（）

A、 $\frac{1}{x - y}$ B、 $\frac{4}{8 a}$ C、 $\frac{x - y}{x^{2} - y^{2}}$ D、 $\frac{x^{2} - x}{x}$

查看试题解析
4. 下列等式中，从左到右的变形属于因式分解的是（）

A、 $(x + 1) (x + 2) = x^{2} + 3 x + 2$ B、 $x^{2} - 4 x + 5 = (x - 2)^{2} + 1$ C、 $x^{2} - 9 = (x + 3) (x - 3)$ D、 $x^{2} + 5 x + 6 = x (x + 5) + 6$

查看试题解析
5. 如图1，战国时期《考工记》详细记载了用几何方法校验轮轴支架（“轸”）为平行四边形的技术：“凡察车之道，必自载于地者始也.合矩以为方，中规乃行”.如图2，实际操作为：构成轮轴支架四边形的顶点分别为A，B，C，D，若 $A O = C O$ ，且 $B O = D O$ ，则轮轴支架形成的四边形是平行四边形的最简明理由是（）

A、对角线互相平分 B、两组对边分别相等 C、一组对边平行且相等 D、两组对边分别平行

查看试题解析
6. 如图，一次函数 $y_{1} = x + b$ (b是常数)，与正比例函数 $y_{2} = k x$ (k是常数， $k \neq 0$ ) 的图象相交于点 M(2， 1)，则关于x的不等式 $k x > x + b$ 的解集是（）

A、 $x > 2$ B、 $x \geq 2$ C、 $x < 2$ D、 $x \leq 2$

查看试题解析
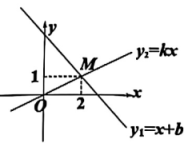7. 某企业要购进两款机器狗共5只.如图所示，已知 Cyber Dog 2 单价是 1.3 万元/只，Unitree Go 2 单价是 1 万元/只，且该企业购进两款机器狗的总费用不超过 6.2 万元，则 Cyber Dog 2 最多可以购进（）

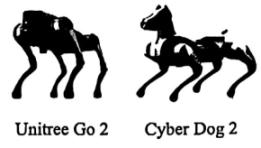A、1 只 B、2 只 C、3 只 D、4 只

查看试题解析
8. 如图，在 $△ A B C$ 中， $A B = A C = 2$ ， $∠ B A C = 12 0^{°}$ ，将BC边绕着点A逆时针旋转90°，旋转后的对应线段B'C'与BC边交于点E，连接AE，则AE的长为（）

A、1 B、 $\sqrt{2}$ C、 $\frac{2 \sqrt{3}}{3}$ D、 $\sqrt{3}$

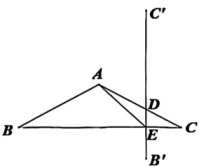查看试题解析

二、填空题(本题共5小题，每小题3分，共15分.

9. 因式分解：x²-x= ．

查看试题解析
10. 如图，八角窗花的窗格是中国古代建筑中一抹独到的风景，其外观是一个正八边形，则它的每一个外角为 $^{°}$ .

查看试题解析
11. 如果不等式组 ${\begin{array}{l} x + 8 < 4 x - 1 \\ x > m \end{array}$ 的解集是 $x > 3$ ，则 m 的值可以是（写出一个符合要求的值即可）.

查看试题解析
12. 如图，平行四边形ABCD的面积为7，对角线AC，BD交于点O，线段EF经过点O，交AD于点E，交BC于点F，则阴影部分面积为 .

查看试题解析
13. 如图，点P是长方形ABCD边上的一个动点，从A点开始，沿 $A \to D \to C \to B \to A$ 顺时针运动一周，运动速度是1cm/s.当运动时间t为5s或35s时，点P均满足 $P B = P D$ ，则AB的长为 cm.

查看试题解析

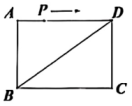
三、解答题(本题共7小题，其中第14题8分，第15题6分，第16题8分，第17题9分，第18题8分，第19题10分，第20题12分，共61分)

14. 下面是小明解不等式， ${\begin{array}{l} \frac{1 - 2 x}{3} + 1 \geq 0, \\ 3 (1 - x) > 2 x - 4 \end{array}$ 的过程，请认真阅读并完成相应的任务.
解：不等式①，去分母，得 $1 - 2 x + 3 \geq 0$ ，（第一步）
移项，合并同类项，得 $- 2 x \geq - 4$ ，（第二步）
系数化为1，得 $x \geq 2$ ，（第三步）
解不等式②，得 $x < \frac{7}{5}$ ，（第四步）|
所以原不等式组无解. （第五步）
根据以上材料，解答下列问题：

(1)、第一步去分母的依据是.

(2)、在解答过程中，从第步开始出错，错误原因是.

(3)、解不等式组： ${\begin{array}{l} \frac{1 - 2 x}{3} + 1 \geq 0, \\ 3 (1 - x) > 2 x - 4 \end{array}$

查看试题解析
15. 先化简，再求值： $(x + 2 - \frac{5}{x - 2}) + \frac{x - 3}{x^{2} - 4 x + 4}$ ，其中 $x = 1$ .

查看试题解析
16. 如图，在平面直角坐标系中， $△ A B C$ 的三个顶点坐标分别为 A(3，4)，B(4，1)，C(1，2).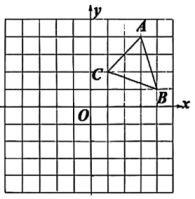
⑴ 将 $△ A B C$ 先向左平移 4 个单位长度，再向下平移 1 个单位长度，得到 $△ A_{1} B_{1} C_{1}$ ，其中点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的对应点分别是 $A_{1}$ ， $B_{1}$ ， $C_{1}$ ，请在图中画出 $△ A_{1} B_{1} C_{1}$ ；
⑵将 $△ A B C$ 绕点 (0，0) 顺时针旋转 $9 0^{°}$ 得到图形 $△ A_{2} B_{2} C_{2}$ ，其中点 $A_{2}$ ， $B_{2}$ ， $C_{2}$ 的对应点分别是 $A_{2}$ ， $B_{2}$ ， $C_{2}$ ，请在图中画出 $△ A_{2} B_{2} C_{2}$ ；
⑶ 观察线段 $B_{1} C_{1}$ 和线段 $B_{2} C_{2}$ ，它们所在直线的位置关系为 ▲ .

查看试题解析
17. 【阅读材料】
我们知道，多项式 $a^{2} + 2 a b + b^{2}$ 可以因式分解为 $(a + b)^{2}$ .当一个二次三项式(如 $a^{2} + 6 a + 8$ )不是完全平方式时，我们可以采用下面的方法进行因式分解：
$a^{2} + 6 a + 8 = (a^{2} + 6 a + 9) - 9 + 8$
$= (a + 3)^{2} - 1$
$= [(a + 3) + 1] [(a + 3) - 1]$
$= (a + 4) (a + 2)$ .
【解决问题】请仿照上面的方法，完成下列试题：

(1)、填空：
$a^{2} - 2 a - 3 = (a^{2} - 2 a +$ ①) -② $- 3$
= $(a - 1)^{2} - 4 = [(a - 1) + 2] [(a - 1) - 2]$
$= (a + 1) (a - 3)$ .
$a^{2} - 6 a + 5 = a^{2} - 6 a +$ ③ -④+ 5 $= (a - 3)^{2} - 4 = (a - 1) (a - 5)$ .

(2)、将下列各式因式分解：
① $a^{2} - 4 a + 3 =$ ▲；
② $x^{2} - 2 n x + n^{2} - 4$ .

查看试题解析
18. 已知平行四边形 ABCD.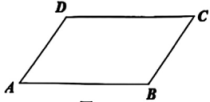

(1)、如图所示，请你用无刻度的直尺和圆规在 CD 边上找一个点 F，使得点 F 到直线 AD 和直线 AB 的距离相等；(请保留作图痕迹，不写作法)

(2)、连接 BF，若 $B F ⊥ C D$ ， $A D = 5$ 且 $B F = 4$ ，请你求出平行四边形 ABCD 的面积.

查看试题解析
19. 深圳福田区部分小区，如图1，居民可通过智能回收箱扫描二维码投放废纸和废塑料，废品回收可实现资源循环利用.某学习小组对一批回收废纸和回收废塑料进行了调查，相应数据如下：
名称
每吨生产再生纸
数量（单位：吨）
共生产再生纸
废纸
x
①
16吨
名称
每吨可回炼无铅汽油
数量（单位：吨）
共回炼无铅汽油
废塑料
②
③
18吨

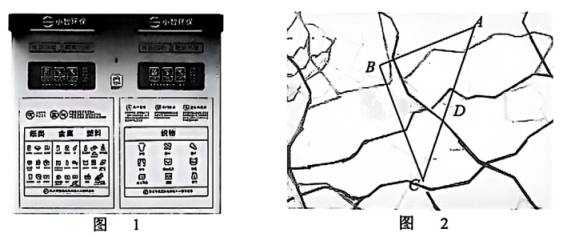
(1)、任务一：现回收废纸和废塑料共 50 吨，已知每吨废塑料回炼的无铅汽油量是每吨废纸生产再生纸数量的 $\frac{3}{4}$ 倍，设每吨废纸可生产 x 吨再生纸，请补全表格数据（用含 x 的代数式表示）；

(2)、任务二：请求出（1）中 x 的值；

(3)、任务三：如图 2，在某区的智能回收箱运营体系中，点 A 为清运回收点，点 B 为分拣点，点 C 为打包点，点 D 为回收加工点，且满足： $A B ⊥ B C$ ， $A B = 6$ 千米， $B C = 8$ 千米，AB 的垂直平分线 DF 与 AC 交于点 D.将各点位置简化为图3.现需在 BC 边上设置智能回收运营点 G，使得点 G 到点 A，B，C，D 四个流程点的距离之和最小，请求出其最小值.

查看试题解析
20. 【特例研究】

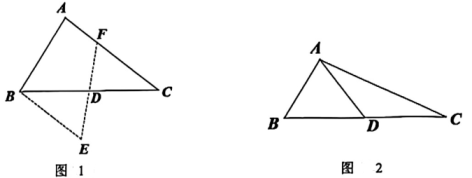(1)、在 $△ A B C$ 中，点 D 是 BC 的中点，
①如图 1，点 F 是 AC 边上的一点，连接 FD 并延长FD 至点 E，使得 $D E = F D$ ，连接 BE，求证： $F C ∥ B E$ 且 $F C = B E$ ；
②如图 2，若 $A B = 3$ ， $A C = 6$ ， AD的取值范围为 ▲ .

(2)、【拓展延伸】
如图 3，线段 $A B = 10$ ，过点 B 作一条射线 BC，使得 $∠ A B C = 12 0^{°}$ ，动线段 EF 在射线 BC 上运动（点 E 在点 F 的下方），且 $E F = A B$ ，点 D 是 AF 的中点，连接 DE.
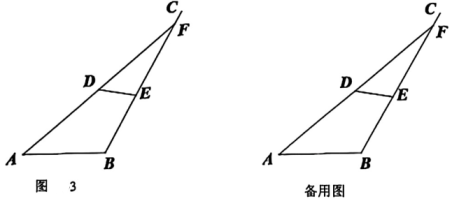
①请求出 DE 的最小值；
②当 BE 等于多少时， $∠ D E B = 4 5^{°}$ ？请说明理由.

查看试题解析

名称	每吨生产再生纸	数量（单位：吨）	共生产再生纸
废纸	x	①	16吨
名称	每吨可回炼无铅汽油	数量（单位：吨）	共回炼无铅汽油
废塑料	②	③	18吨