广东省深圳市福田区2024-2025学年七年级下学期数学期末教学质量检测

试卷更新日期：2025-07-10 类型：期末考试

进入出卷网下载

一、选择题(本题共8小题，每小题3分，共24分，每小题给出4个选项，其中只有一个是正确的)

1. 下列人工智能应用图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 某款无人机的影像传感器像素点间距为0.0000024米，能够捕捉到丰富的细节.数据0.0000024用科学记数法表示为（）

A、 $2.4 \times 1 0^{- 5}$ B、 $2.4 \times 1 0^{- 6}$ C、 $24 \times 1 0^{- 7}$ D、 $0.24 \times 1 0^{- 5}$

查看试题解析
3. 小福每天早上七点在站台等候搭乘公共汽车，他把每天等待上车的时间整理如下：
等候次数
10
20
50
100
200
300
等待上车的时间少于5min的次数
5
13
38
79
162
240
等待上车的时间少于5min的频率
0.50
0.65
0.76
0.79
0.81
0.80
小福再等一次公共汽车，等待上车的时间少于5min 概率是（）

A、0.5 B、0.6 C、0.7 D、0.8

查看试题解析
4. 下列运算正确的是（）

A、 $(a^{2})^{3} = a^{6}$ B、 $a^{2} + a^{3} = a^{5}$ C、 $a^{2} \cdot a^{3} = a^{6}$ D、 $(a b)^{5} = a b^{5}$

查看试题解析
5. 图1 是视觉错觉艺术风格的作品，这种设计利用背景线条、图案的干扰，制造出视觉认知偏差的冲突，具有很强的趣味性与迷惑性.如图2，现将其中的一组背景线条与直线a，b抽象出来，下列说法能判断出 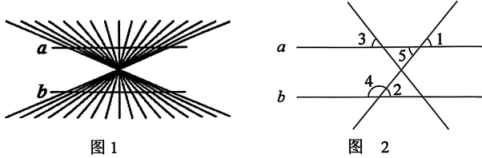$a ∥ b$ 的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 1 = ∠ 5$ C、 $∠ 2 + ∠ 4 = 18 0^{°}$ D、 $∠ 2 = ∠ 3$

查看试题解析
6. 某款自行车的三角形车架中，有两根钢架长分别为5分米和8分米，则第三根的长可能是（）

A、3分米 B、9分米 C、13分米 D、15分米

查看试题解析
7. 图是一段双向等宽道路，点A，B是马路两边正对面的两个公交站牌，点E是隔离带EF中的一个花坛， $A C ∥ B D ∥ E F$ .小田所在点C，学校门口D和花坛E在同一条直线上.小田测量出点A，C之间的距离是18m，就可知道学校门口D与公交站牌B之间的距离为18m.此方案的依据是（）

A、SSS B、ASA C、SSA D、SAS

查看试题解析
8. 如图1，2025年首届具身智能机器人运动会在江苏省无锡市举办.某研发公司为了测试某新型智能机器人的竞速跑情况，在一条笔直的跑道上设置了甲、乙、丙三个测试点.该机器人从甲处以1.5m/s的速度匀速跑到乙处，停留一会儿后，再以2m/s的速度匀速跑到丙处，停留15s后，从丙处匀速返回甲处.该机器人离测试点甲的距离y(m)与离开测试点甲的时间x(s)之间的关系如图2所示，下列说法错误的是（）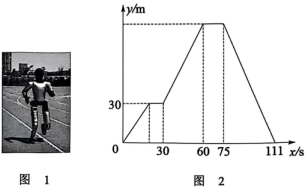

A、该机器人从测试点甲到测试点乙用了20s B、该机器人在测试点乙处停留了10s C、测试点乙与测试点丙之间的距离为60m D、该机器人从测试点丙返回到测试点甲的速度为2.7m/s

查看试题解析

二、填空题(本大题共5小题，每小题3分，共15分)

9. 计算： $2 m (m + 1) =$ .

查看试题解析
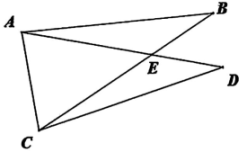
10. 如图， $∠ A C B = ∠ C A D$ ，要使 $△ A C B ≅ △ C A D$ ，还需要添加一个条件是 (添加一个即可).

查看试题解析
11. 如图，把一块直角三角尺的直角顶点放在直尺的一边上，若 $∠ 1 = 3 2^{°}$ ，则 $∠ 2$ 的度数是.

查看试题解析
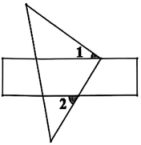12. 如图，四边形 ABCD 的面积是 10，各边的中点分别为 M，N，P，Q，MP 与 NQ 相交于点 O，图中阴影部分的总面积为.

查看试题解析
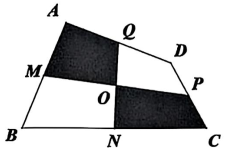13. 转化是解决数学问题的一种重要策略，可将不规则的图形转化为规则图形，达到化繁为简、化难为易、化不熟悉为熟悉的目的.如图，是两个部分重合的等腰直角三角形，腰长分别为a，b(a>b)，a+b=7，a-b=2，阴影部分面积分别为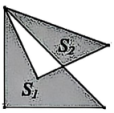 $S_{1}$ ， $S_{2}$ ，则 $S_{1} - S_{2}$ =.

查看试题解析

三、解答题(本题共7小题，其中第14题10分，第15题7分，第16题8分第17题8分，第18题8分，第19题9分，第20题11分，共61分)

14. 计算：

(1)、 $4 \times (- 2)^{- 2} - (- 1)^{2025} + (π - 3)^{0}$ ；

(2)、 $3 m^{2} \cdot m^{4} + (2 m^{3})^{2}$ .

查看试题解析
15. 先化简，再求值： $[(x + y)^{2} - (x + 3 y) (x - 3 y)] + 2 y$ ，其中 $x = 2$ ， $y = 1$ .

查看试题解析
16. 如图，在 $△ A B C$ 中，点D，E分别在边AB和AC上，过点C作 $C F ∥ A B$ 交DE的延长线于点F， $∠ D E C + ∠ A C B = 18 0^{°}$ ，

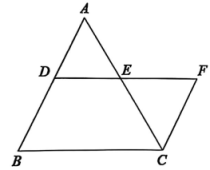(1)、试说明： $∠ B = ∠ F$ （将过程补充完整，并写出每一步的推理依据）
解： ∵ $∠ D E C + ∠ A C B = 18 0^{°}$ ，（已知）
∴ $D F ∥ B C$ ，（ ▲ ）
∴ $∠ B = ∠ A D E$ ，（ ▲ ）
∴ ▲ ，（已知）
∴ $∠ A D E =$ ▲ ，（ ▲ ）
∴ $∠ B = ∠ F$ .（等量代换）

(2)、若 $∠ C E F = 7 0^{°}$ ， $∠ A = 4 5^{°}$ ，求 $∠ B C F$ 的度数.

查看试题解析
17. 某景区向雪糕厂定制了一批包装相同的文创盲盒雪糕在景区小卖部售卖，其中巧克力口味50个，芒果口味40个，香蕉口味30个.

(1)、小方从景区小卖部买一个雪糕，能买到巧克力口味是一个事件(填写“必然”、“随机”、“不可能”)

(2)、小程从景区小卖部买了一个雪糕，是芒果口味的概率是多少？

(3)、因天气炎热，第一批雪糕供不应求，景区准备定制第二批雪糕，原计划各口味定制的数量与第一批定制的相同.后来，为了让旅客买到巧克力口味的概率为 $\frac{1}{2}$ ，需把部分香蕉口味的雪糕替换成巧克力口味，求替换的雪糕数量.

查看试题解析
18. 如图，点E，A，D，B在同一条直线上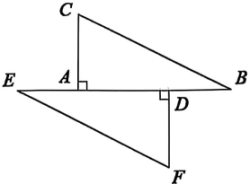， $∠ C A B = ∠ F D E = 9 0^{°}$ ， $D B = A E$ ， $B C ∥ E F$ .

(1)、 $△ A B C$ 与 $△ D E F$ 全等吗？请说明理由；

(2)、尺规作图：作 $∠ B$ 的角平分线，与AC交于点P（不要求写作法，保留作图痕迹）；

(3)、在条件（2）下，若 $E F = 6$ ， $A P = \frac{5}{2}$ ，求 $△ P B C$ 的面积.

查看试题解析
19. 综合与实践——万花筒里的数学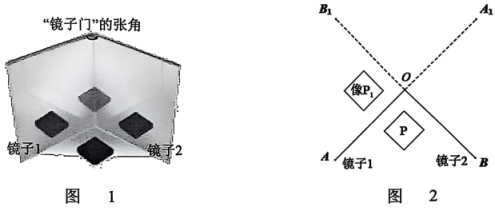
【发现问题】如图1，学习小组在制作万花筒时，先将两面平面镜的背面用胶带粘贴，形成一个可以自由开合的“镜子门”，发现观察到的图形数量与“镜子门”张角的大小有关，进而研究此规律.
【查阅资料】平面镜成像原理：物体与它在平面镜中的像关于平面镜成轴对称
【数学探究】
探究一：如图2，正方形 P 放在“镜子门”中间，当“镜子门”张角 $∠ A O B$ 为 $9 0^{°}$ 时，正方形 P 关于镜子 OA 的轴对称图形是像 $P_{1}$ .

(1)、请你画出正方形 P 在镜子 OB 中的像 $P_{2}$ （不限作图工具）；

(2)、像 $P_{1}$ ，像 $P_{2}$ 会在镜子中再次轴对称成像，像 $P_{1}$ 关于 $O B_{1}$ 的轴对称图形是像 $P_{3}$ ，像 $P_{2}$ 关于 $O A_{1}$ 的轴对称图形是像 $P_{4}$ ，请分析像 $P_{3}$ 与像 $P_{4}$   重合（填写“是”或“否”）.

(3)、探究二：如图3，当“镜子门”张角 $∠ A O B$ 大小是 $36 0^{°}$ 的因数时，观察到的图形数量（包含实物与像，重合的像看作一个像）是有规律的.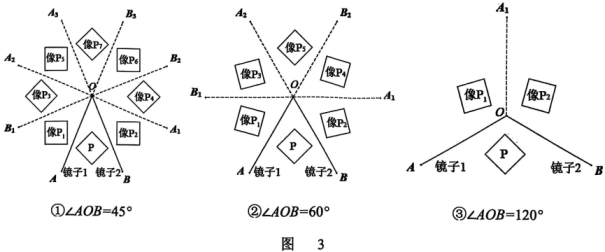
改变张角 $∠ A O B$ 的大小，并记录观察到的图形数量，得到以下表格：
$∠ A O B$ 的度数x/度
45
60
72
90
120
观察到的图形数量y/个
8
6
▲
4
3
①在这个变化过程中，    ▲    是自变量，    ▲    是因变量；
②补充上述表格；
③请写出观察到的图形数量y与 $∠ A O B$ 的度数x的关系式：    ▲    .

查看试题解析
20. 定义：两个不全等的三角形，若有一组公共边和一个公共角，且公共角所对的边相等，我们就称这两个三角形为“双赢三角形”.例如，在图 1 中， $△ M P Q$ 与 $△ M P N$ 有公共边 MP 和公共角 $∠ M$ ，且 $P Q = P N$ ，则 $△ M P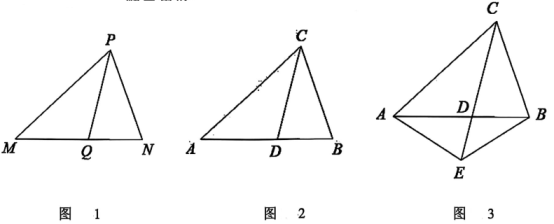 Q$ 与 $△ M P N$ 是双赢三角形.
如图2，在 $△ A B C$ 中，D 是 AB 边上任意一点，

(1)、若 $△ A C D$ 和 $△ A C B$ 是“双赢三角形”， $∠ B C D = 4 2^{°}$ ，则 $∠ B$ = ；

(2)、如图3，延长 CD 到点 E，连接 AE 和 BE， $∠ A C D = ∠ E C B$ ， $∠ C D B + ∠ C B E = 18 0^{°}$ ， $A D = E B$ ，
① 试说明： $△ A C D$ 与 $△ A C B$ 是“双赢三角形”；
② 若 $B C = 12$ ， $A C = 18$ ，求 DE 的长；
③ 若 $∠ C A B = 5 4^{°}$ ， $∠ A B C = 7 8^{°}$ ，求 $∠ A E B$ 的度数.

查看试题解析

等候次数	10	20	50	100	200	300
等待上车的时间少于5min的次数	5	13	38	79	162	240
等待上车的时间少于5min的频率	0.50	0.65	0.76	0.79	0.81	0.80

$∠ A O B$ 的度数x/度	45	60	72	90	120
观察到的图形数量y/个	8	6	▲	4	3