广东省深圳市罗湖区2024-2025学年七年级下学期数学期末质量检测
试卷更新日期:2025-07-10 类型:期末考试
一、单选题
-
1. 甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,不是轴对称的是( )A、
 B、
B、 C、
C、 D、
D、 2. 我国知名华为技术有限公司最新上市的mate70系列搭载了麒麟9000s芯片,这个被华为称之为全球首个5纳米工艺的AI芯片,拥有8个全球第一,5纳米就是0.000000005米,数据0.000000005用科学记数法表示应为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,A,B,C,D四点在直线l上,点M在直线l外, , 若 , , , 则点M到直线l的距离是( )
2. 我国知名华为技术有限公司最新上市的mate70系列搭载了麒麟9000s芯片,这个被华为称之为全球首个5纳米工艺的AI芯片,拥有8个全球第一,5纳米就是0.000000005米,数据0.000000005用科学记数法表示应为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,A,B,C,D四点在直线l上,点M在直线l外, , 若 , , , 则点M到直线l的距离是( )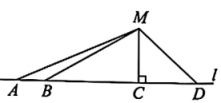 A、2cm B、3cm C、4cm D、5cm5. 下列说法中正确的是( )A、种植一种花卉成活率是 , 则种100株这种花一定会有95株成活 B、天气预报“明天降水概率是”是指明天有的时间会下雨 C、某位体育老师参加深圳市半程马拉松比赛一定能获得大奖 D、随机掷一枚质地均匀的骰子,若前3次都掷出“1”,则第4次仍然可能掷出“1”6. 漏刻是我国古代的一种计时工具.小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现了水位h(单位:cm)和时间t(单位:min)两个变量之间的关系.下表是小明记录的部分数据,当h为10cm时,对应的时间t为( )
A、2cm B、3cm C、4cm D、5cm5. 下列说法中正确的是( )A、种植一种花卉成活率是 , 则种100株这种花一定会有95株成活 B、天气预报“明天降水概率是”是指明天有的时间会下雨 C、某位体育老师参加深圳市半程马拉松比赛一定能获得大奖 D、随机掷一枚质地均匀的骰子,若前3次都掷出“1”,则第4次仍然可能掷出“1”6. 漏刻是我国古代的一种计时工具.小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现了水位h(单位:cm)和时间t(单位:min)两个变量之间的关系.下表是小明记录的部分数据,当h为10cm时,对应的时间t为( )t/min
...
1
2
3
4
...
h/cm
...
2.4
2.8
3.2
3.6
...
 A、10min B、12min C、16min D、20min7. 如图,直线 , 将直角三角板的直角顶点放在直线b上. 若 , 则的度数为( )
A、10min B、12min C、16min D、20min7. 如图,直线 , 将直角三角板的直角顶点放在直线b上. 若 , 则的度数为( )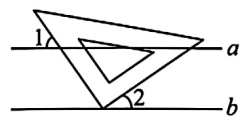 A、 B、 C、 D、8. 如图,在的正方形网格中,线段AB,CD的端点均在格点上,则和的数量关系是( )
A、 B、 C、 D、8. 如图,在的正方形网格中,线段AB,CD的端点均在格点上,则和的数量关系是( )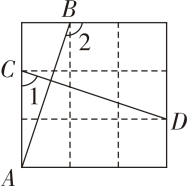 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,飞镖游戏板由大小相等的小正方形格子构成,小东向游戏板随机投掷一枚飞镖,击中黑色区域的概率是 .
 10. 若 , 则m的值是.11. 如图是小颖同学劳动节前夕,在街上拍到的路灯维护工程车的工作示意图,工作篮底部与支撑平台平行,若 , , 则的度数为.
10. 若 , 则m的值是.11. 如图是小颖同学劳动节前夕,在街上拍到的路灯维护工程车的工作示意图,工作篮底部与支撑平台平行,若 , , 则的度数为.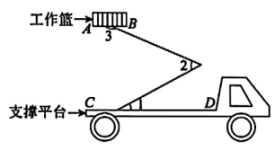 12. 如上图,公园里有一座假山,要测量假山两端 A、B 的距离,先在平地上取一个可以直接到达 A、B 的点 C,分别延长 AC、BC 到 D、E,使 , , 连接 DE,这样就可以利用三角形全等,通过测量 DE 的长得到假山两端 A、B 的距离,则判定这两个三角形全等的依据是.
12. 如上图,公园里有一座假山,要测量假山两端 A、B 的距离,先在平地上取一个可以直接到达 A、B 的点 C,分别延长 AC、BC 到 D、E,使 , , 连接 DE,这样就可以利用三角形全等,通过测量 DE 的长得到假山两端 A、B 的距离,则判定这两个三角形全等的依据是.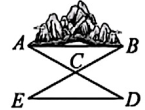 13. 如图,在中, , 和的平分线相交于点 , 交AC于 , 交BC于 , , , , 则周长为.
13. 如图,在中, , 和的平分线相交于点 , 交AC于 , 交BC于 , , , , 则周长为.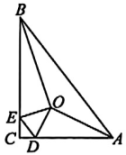
三、解答题
-
14. 计算:.15. 先化简,再求值: , 其中x=-2, .16. 随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷. 为此,某团队设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种)进行随机调查. 将统计结果绘制了如图所示的两幅不完整的统计图,请结合图中所给的信息解答下列问题:
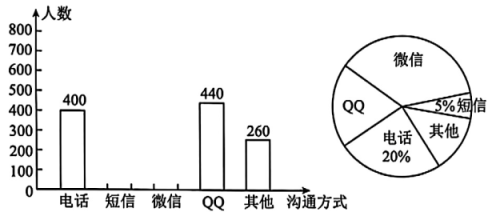 (1)、 这次参与调查的共有人;在扇形统计图中,表示“微信”的扇形圆心角的度数为°;(2)、 将条形统计图补充完整;(3)、 如果某市有 1000 万人在使用手机:
(1)、 这次参与调查的共有人;在扇形统计图中,表示“微信”的扇形圆心角的度数为°;(2)、 将条形统计图补充完整;(3)、 如果某市有 1000 万人在使用手机:①则估计该市最喜欢用“微信”进行沟通的人数为万人;
②在该市使用手机的人中随机抽取一人,用频率估计概率,则抽取的最喜欢使用“QQ”沟通的概率是.
17. 如图,科技改变世界,为提高快递包裹分拣效率,物流公司引进了快递自动分拣流水线,如图①所示,图②是将部分流水线抽象而成的数学模型示意图.如图②,已知: , OE平分 , CF平分.试说明:.阅读下面的解答过程,并填空(理由或数学式).
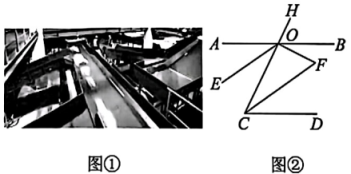
解:∵(已知),
∴ = ▲ ( ▲ ).
∵OE平分∠AOC(已知),
∴ ▲ ( ▲ ).
同理 ▲ ( ▲ ).
∴( ▲ ),
∴ ▲ ( ▲ ).
∴( ▲ ).
18. 某校为了选拔百米运动员,让学生进行百米比赛,小明和小亮同时起跑,比赛情况如图所示,其中横轴表示时间t(s),纵轴表示距起跑点的距离s(m),根据图象回答下列问题.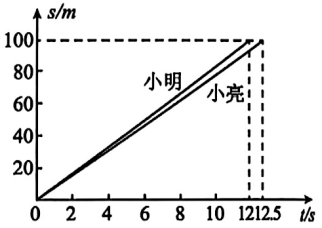 (1)、 小明和小亮的百米成绩各是多少?(2)、 两人的速度各是多少?(3)、 当小明到达终点时,小亮所跑的路程是多少?19. (学习情境·动手操作)综合与实践课上,同学们动手折叠一张正方形纸片ABCD,如图1,其中E点在边AD上,F、G分别在边AB、CD上,分别以EF、EG为折痕进行折叠并压平,点A、D的对应点分别是点和点.
(1)、 小明和小亮的百米成绩各是多少?(2)、 两人的速度各是多少?(3)、 当小明到达终点时,小亮所跑的路程是多少?19. (学习情境·动手操作)综合与实践课上,同学们动手折叠一张正方形纸片ABCD,如图1,其中E点在边AD上,F、G分别在边AB、CD上,分别以EF、EG为折痕进行折叠并压平,点A、D的对应点分别是点和点.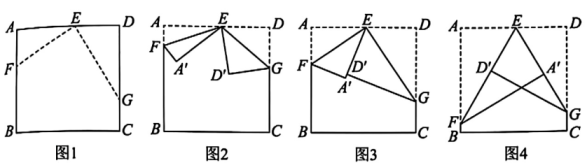
甲同学的操作如图2,其中;
乙同学的操作如图3,A'落在所在直线上;
丙同学的操作如图4,A'落在EG上,落在EF上.
【阅读理解】
(1)、 图2中的度数为;(2)、 图3中 ;(3)、 图4中的度数为 ;(4)、 若折叠后 , 求的度数(用含n的代数式表示),且说明理由.20. 【模型呈现】“数学区别于其它学科最主要的特征是抽象与推理”.“一线三等角”模型是几何世界中常见的模型之一,只要细心观察,你就可以从中找到全等三角形.
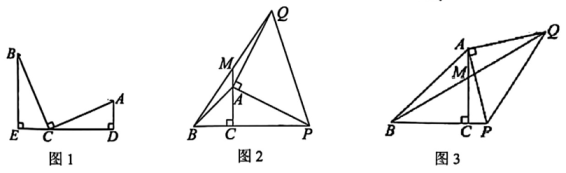 (1)、 【模型理解】如图1,已知,点C在线段DE上, , 若 , 则BE与CD的数量关系为 , BE, AD与DE的数量关系为;(2)、 【拓展延伸】在Rt中, , 分别以AC、AP为腰,在左侧作等腰直角三角形ABC,在右侧作等腰直角三角形APQ,其中 , ,
(1)、 【模型理解】如图1,已知,点C在线段DE上, , 若 , 则BE与CD的数量关系为 , BE, AD与DE的数量关系为;(2)、 【拓展延伸】在Rt中, , 分别以AC、AP为腰,在左侧作等腰直角三角形ABC,在右侧作等腰直角三角形APQ,其中 , ,① 如图2,连接BQ,当交线段CA的延长线于点M时,求证:;
② 如图3,连接BQ,当交线段CA于点M,且时,求BP的长.