四川成都市郊区联考2024-2025学年七年级下学期数学期末试卷
试卷更新日期:2025-07-09 类型:期末考试
一、A卷,选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)
-
1. 许多高校的校微设计都蕴含着数学的美感,下列四所高校校徽主体图案是轴对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 下列事件中,说法正确的是( )A、打开电视,正在播放动画片是必然事件 B、两直线平行,同旁内角相等 C、三条线段的长分别是3,4,7,正好能构成三角形 D、同位角相等,两直线平行3. 如图,将木条a,b与c钉在一起,∠1=68°,∠2=51°,要使木条a与b平行,木条a需顺时针旋转的度数是( )
A、1个 B、2个 C、3个 D、4个2. 下列事件中,说法正确的是( )A、打开电视,正在播放动画片是必然事件 B、两直线平行,同旁内角相等 C、三条线段的长分别是3,4,7,正好能构成三角形 D、同位角相等,两直线平行3. 如图,将木条a,b与c钉在一起,∠1=68°,∠2=51°,要使木条a与b平行,木条a需顺时针旋转的度数是( )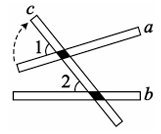 A、13° B、15° C、17° D、19°4. 下列运算中,正确的是( )A、3a2-a2=2a B、(a+b)2=a2+b2 C、a3b2÷a2=a D、(a2b)2=a4b25. 如图,若△ABC≌△ADE,则下列结论中不成立的是( )
A、13° B、15° C、17° D、19°4. 下列运算中,正确的是( )A、3a2-a2=2a B、(a+b)2=a2+b2 C、a3b2÷a2=a D、(a2b)2=a4b25. 如图,若△ABC≌△ADE,则下列结论中不成立的是( )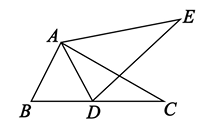 A、BC=DE B、∠BAD=∠CDE C、DA平分∠BAE D、∠CAE=∠CDE6. 通过实验发现凸透镜能使与主光轴平行的光线聚在主光轴上一点,如图,箭头所画的是光线的方向,点F是凸透镜的焦点,AC//BD//OF,若∠ACF=151°,∠BDF=160°,则∠CFD的度数是( )
A、BC=DE B、∠BAD=∠CDE C、DA平分∠BAE D、∠CAE=∠CDE6. 通过实验发现凸透镜能使与主光轴平行的光线聚在主光轴上一点,如图,箭头所画的是光线的方向,点F是凸透镜的焦点,AC//BD//OF,若∠ACF=151°,∠BDF=160°,则∠CFD的度数是( )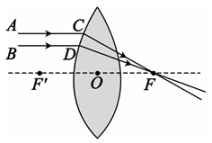 A、9° B、10° C、11° D、12°7. “儿子学成今日返,儿子已到父未到,父亲到后细端详,父子高兴把家还,”如图,用y轴表示父亲与儿子行进中离家的距离,用x轴表示父亲离家的时间,那么下列图象与上述诗的含义大致相吻合的是( )A、
A、9° B、10° C、11° D、12°7. “儿子学成今日返,儿子已到父未到,父亲到后细端详,父子高兴把家还,”如图,用y轴表示父亲与儿子行进中离家的距离,用x轴表示父亲离家的时间,那么下列图象与上述诗的含义大致相吻合的是( )A、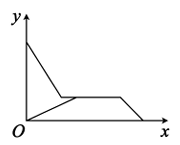 B、
B、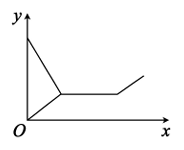 C、
C、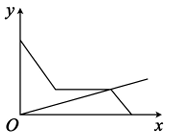 D、
D、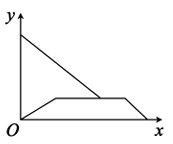 8. 我国南宋数学家杨辉在所著的《详解九章算术》一书中,用如图的三角形给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序)的系数规律,例如:此三角形中第3行的3个数1、2、1,恰好对应着(a+b)2=a2+2ab+b2展开式中的各项的系数,则(a+b)2025的展开式所有项的系数和是( )
8. 我国南宋数学家杨辉在所著的《详解九章算术》一书中,用如图的三角形给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序)的系数规律,例如:此三角形中第3行的3个数1、2、1,恰好对应着(a+b)2=a2+2ab+b2展开式中的各项的系数,则(a+b)2025的展开式所有项的系数和是( )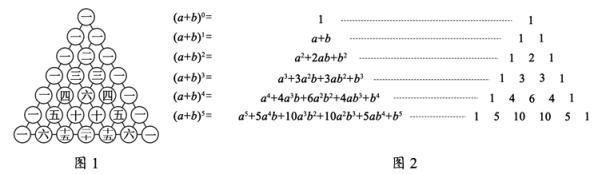 A、4050 B、20242 C、22024 D、22025
A、4050 B、20242 C、22024 D、22025二、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
-
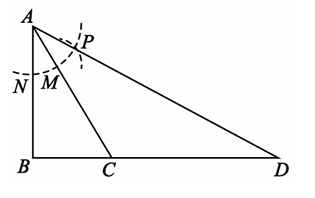
9. 计算:8x2y÷(-2x)2=.10. 已知方程35x-y+20=0,用含x的代数式表示y的形式为.11. 在直角三角形中,较小锐角的度数是较大锐角的度数的 , 较大锐角的度数为.12. A和B两个纸箱中装有苹果和梨.A中苹果有m个,梨8个,B中苹果有10个,梨n个,从两个纸箱中摸出苹果的概率均为 , 则m+n=.13. 如图,在Rt△ABC中,∠B=90°,以点A为圆心,任意长为半径画弧分别交AB,AC于点N和M,再以点M为圆心,线段MN为半径画弧,两弧交于点P,连接AP并延长,交BC的延长线于点D.如果∠ACB=66°,则∠D=.
三、解答题(本大题共5个小题,共48分,解答过程写在答题卡上)
-
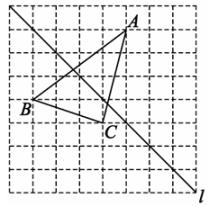
14. 计算下列各题:(1)、;(2)、.15. 先化简,再求值:[(x+2y)2-(3x+y)(3x-y)-5y2]÷(-2x),其中x=-2,y=1.16. 如图,在长度为1个单位长度的小正方形组成的正方形网格中,△ABC的三个顶点A,B,C都在格点上.
 (1)、画出△ABC关于直线l成轴对称的△A1B1C1;(2)、求△ABC的面积;(3)、在直线l上找一点P使得A1P+CP的值最小,并标出点P位置.17. 某校在劳动手工课上需要给作品添加花边,学生将长为20cm,宽为10cm的长方形彩纸按图所示的方法黏合起来,黏合部分的宽为2cm.
(1)、画出△ABC关于直线l成轴对称的△A1B1C1;(2)、求△ABC的面积;(3)、在直线l上找一点P使得A1P+CP的值最小,并标出点P位置.17. 某校在劳动手工课上需要给作品添加花边,学生将长为20cm,宽为10cm的长方形彩纸按图所示的方法黏合起来,黏合部分的宽为2cm.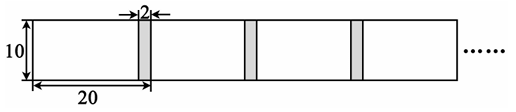 (1)、根据题意,将表格补充完整;
(1)、根据题意,将表格补充完整;彩纸张数/张
1
2
3
4
5
……
纸条长度/cm
20
56
74
……
(2)、设x张彩纸黏合后的总长度为y厘米,写出y与x之间的关系式,并求出50张彩纸黏合后的总长度;(3)、若彩纸黏合后的总长度为2702cm,请问需要多少张彩纸?18. 如图,在等腰△ABC中,AB=AC,点D在BC的延长线上,∠ADB=∠BAC,BE⊥AD交于AC于点F.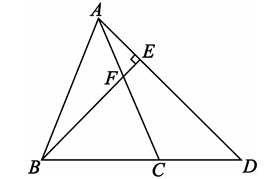 (1)、证明:AD=BD;(2)、若∠CAD=12°,求∠BAC的度数;(3)、若△BCF为等腰三角形,求∠BAC度数.
(1)、证明:AD=BD;(2)、若∠CAD=12°,求∠BAC的度数;(3)、若△BCF为等腰三角形,求∠BAC度数.四、B卷,填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
-
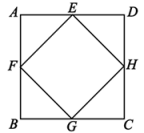
19. 已知2a=16,2b=12,2c=48,则a+b-c=.20. 若 , 则的值为 .21. 如图,在正方形ABCD中,取四条边的中点E,F,G,H,并依次连接形成四边形EFGH.若随机向正方形ABCD内投掷一枚小针,则针尖落在四边形EFGH内的概率为.
 22. 如图,正方形ABCD和正方形CGFE的面积之和为52,若DE=2,则BG=.
22. 如图,正方形ABCD和正方形CGFE的面积之和为52,若DE=2,则BG=.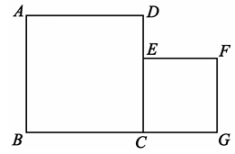 23. 如图,在“问题解决策略:特殊化”课中,小茗同学拿了两块相同的含45°的三角尺,即等腰直角△MNK和等腰直角△ABC做了一个探究活动:将MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=5,此时重叠部分四边形CEMF的面积为.
23. 如图,在“问题解决策略:特殊化”课中,小茗同学拿了两块相同的含45°的三角尺,即等腰直角△MNK和等腰直角△ABC做了一个探究活动:将MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=5,此时重叠部分四边形CEMF的面积为.
五、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)
-
24. 阅读:若x满足(80-x)(x-60)=30,求(80-x)2+(x-60)2的值.
解:设80-x=a,x-60=b,
则(80-x)(x-60)=ab=30,a+b=(80-x)+(x-60)=20,
∴(80-x)2+(x-60)2=a2+b2=(a+b)2-2ab=202-2×30=340.
请仿照上述例子解决下列问题:
(1)、若x满足(20-x)(x-30)=-10,求(20-x)2+(x-30)2的值;(2)、若x满足(2025-x)2+(2024-x)2=2025,求(2025-x)(2024-x)的值;(3)、如图,正方形ABCD的边长为x,AE=25,CG=40,长方形EFGD的面积是600,四边形NGDH和MEDQ都是正方形,四边形PQDH是长方形,求图中阴影部分的面积(用具体的数值表示).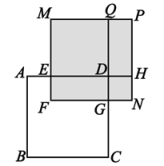 25. 如图1,在四边形ABCD中,AB//CD,∠B=∠C=90°,一点P从点A出发沿着A→B→C→D的方向以每秒2个单位的速度运动,其中CD长为10.在运动过程中,△APD的面积与时间的关系如图2所示.
25. 如图1,在四边形ABCD中,AB//CD,∠B=∠C=90°,一点P从点A出发沿着A→B→C→D的方向以每秒2个单位的速度运动,其中CD长为10.在运动过程中,△APD的面积与时间的关系如图2所示.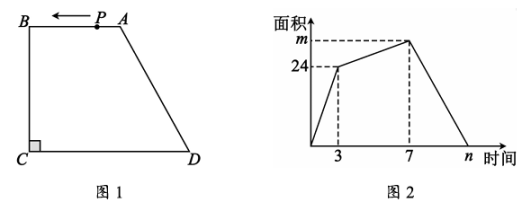 (1)、直接写出AB= , BC=;(2)、求出m与n的值;(3)、在点P的整个运动过程中,若设△APD的面积为S,请求出S与时间t的函数关系式,并写出自变量t的取值范围,26. 如图,△ABC是等边三角形,D为平面内一点,连接AD,将AD绕点D逆时针旋转α度得到线段DE,连接BD,CE.
(1)、直接写出AB= , BC=;(2)、求出m与n的值;(3)、在点P的整个运动过程中,若设△APD的面积为S,请求出S与时间t的函数关系式,并写出自变量t的取值范围,26. 如图,△ABC是等边三角形,D为平面内一点,连接AD,将AD绕点D逆时针旋转α度得到线段DE,连接BD,CE.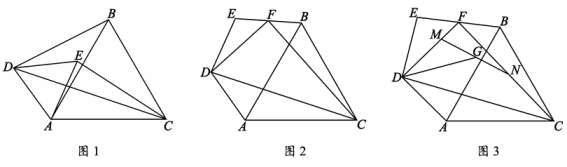 (1)、如图1,若α=60°,求BD和CE的数量关系;(2)、如图2,若α=120°,连接CD,BE,已知F是BE的中点,试判断DF与CF的位置关系并证明;(3)、如图3,在(2)的条件下,M,N分别是DF,CF上的动点,且DM=CN,G是线段MN的中点,连接DG,求当DG取最小值时∠GDC的度数.
(1)、如图1,若α=60°,求BD和CE的数量关系;(2)、如图2,若α=120°,连接CD,BE,已知F是BE的中点,试判断DF与CF的位置关系并证明;(3)、如图3,在(2)的条件下,M,N分别是DF,CF上的动点,且DM=CN,G是线段MN的中点,连接DG,求当DG取最小值时∠GDC的度数.