辽宁省2025年中考真题数学试题
试卷更新日期:2025-07-09 类型:中考真卷
一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)
-
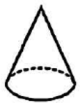
1. 下列几何体中,主视图为三角形的是( )A、
 B、
B、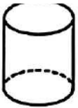 C、
C、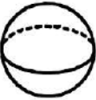 D、
D、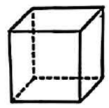 2. 十年砥砺,春华秋实.据2025年5月6日《辽宁日报》报道,辽宁省科学技术馆作为我省重要的科普宣传阵地和科学文化交流平台,自2015年开馆以来,累计接待4超1900万人次.数据19000000用科学记数法表示为( )A、 B、 C、 D、3. 数学中有许多优美的曲线.下列四条曲线既是轴对称图形又是中心对称图形的是( )A、
2. 十年砥砺,春华秋实.据2025年5月6日《辽宁日报》报道,辽宁省科学技术馆作为我省重要的科普宣传阵地和科学文化交流平台,自2015年开馆以来,累计接待4超1900万人次.数据19000000用科学记数法表示为( )A、 B、 C、 D、3. 数学中有许多优美的曲线.下列四条曲线既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、 B、2 C、 D、5. 不透明袋子中仅有红、黄小球各一个,这两个小球除颜色外都相同.从中随机摸出一个小球,记下颜色后,放回并摇匀,再从中随机摸出一个小球,则两次摸出相同颜色的小球的概率为( )A、 B、 C、 D、6. 如图,点C在的边上, , 垂足为D , , 若 , 则 的度数为( )
4. 下列计算正确的是( )A、 B、2 C、 D、5. 不透明袋子中仅有红、黄小球各一个,这两个小球除颜色外都相同.从中随机摸出一个小球,记下颜色后,放回并摇匀,再从中随机摸出一个小球,则两次摸出相同颜色的小球的概率为( )A、 B、 C、 D、6. 如图,点C在的边上, , 垂足为D , , 若 , 则 的度数为( )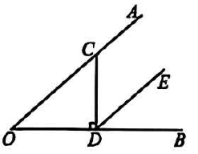 A、50° B、120° C、130° D、140°7. 如图,在矩形中,点在边上, , 连接 , 若 , , 则的长为( )
A、50° B、120° C、130° D、140°7. 如图,在矩形中,点在边上, , 连接 , 若 , , 则的长为( )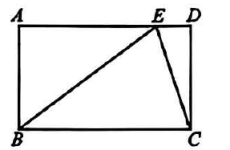 A、1 B、5 C、2 D、8. 在平面直角坐标系xOy中,点的坐标为(3,0),点的坐标为(2,-2),将线段平移得到线段 , 点的对应点的坐标为(3,5),则点的对应点的坐标为( )A、(7,-2) B、(2,3) C、(2,-7) D、(-3,-2)9. 中国古代数学家杨辉的《田亩比类乘除捷法》中记载:“直田积八百六十四步,只云长阔共六十步,问长多阔几何.”其大意是:一块矩形田地的面积为864平方步,只知道它的宽共60步,问它的长比宽多多少步?设这个矩形的宽为步,根据题意可列方程为( )A、 B、 C、 D、210. 如图,在中, , , , 的平分线与相交于点 . 在线段上取一点 , 以点为圆心,长为半径作弧,与射线相交于点和点 , 再分别以点和点为圆心,大于的长为半径作弧,两弧相交于点 , 作射线 , 与相交于点 , 连接 . 则的周长为( )
A、1 B、5 C、2 D、8. 在平面直角坐标系xOy中,点的坐标为(3,0),点的坐标为(2,-2),将线段平移得到线段 , 点的对应点的坐标为(3,5),则点的对应点的坐标为( )A、(7,-2) B、(2,3) C、(2,-7) D、(-3,-2)9. 中国古代数学家杨辉的《田亩比类乘除捷法》中记载:“直田积八百六十四步,只云长阔共六十步,问长多阔几何.”其大意是:一块矩形田地的面积为864平方步,只知道它的宽共60步,问它的长比宽多多少步?设这个矩形的宽为步,根据题意可列方程为( )A、 B、 C、 D、210. 如图,在中, , , , 的平分线与相交于点 . 在线段上取一点 , 以点为圆心,长为半径作弧,与射线相交于点和点 , 再分别以点和点为圆心,大于的长为半径作弧,两弧相交于点 , 作射线 , 与相交于点 , 连接 . 则的周长为( ) A、12 B、14 C、16 D、18
A、12 B、14 C、16 D、18二、填空题(本题共5小题,每小题3分,共15分)
-
11. 在乒乓球质量检测中,如果一只乒乓球的质量超出标准质量记作 , 那么低于标准质量记作 .12. 在电压不变的情况下,电流(单位:)与电阻(单位:)是反比例函数关系.当时, . 则电流与电阻之间的函数表达式为 .13. 甲、乙两名运动员进行跳远测试,每人测试10次,他们各自测试成绩(单位:cm)的平均数和方差如下表:
运动员
平均数
方差
甲
601
95.4
乙
601
243.4
则这两名运动员测试成绩更稳定的是(填“甲”或“乙”).
14. 如图,为了测量树的高度,在水平地面上取一点 , 在处测得 , , 则树的高约为(结果精确到 . 参考数据: , ).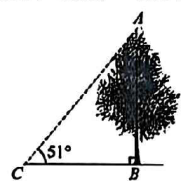 15. 如图,在菱形中,对角线与相交于点 , 点在线段上, , 点在线段上, , 连接 , 点为的中点,连接 , 则的长为 .
15. 如图,在菱形中,对角线与相交于点 , 点在线段上, , 点在线段上, , 连接 , 点为的中点,连接 , 则的长为 .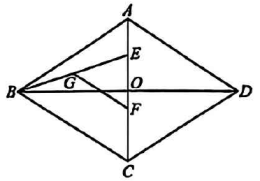
三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)
-
16.(1)、计算:;(2)、计算: .17. 小张计划购进两种文创产品,在“文化夜市”上进行销售.已知种文创产品比种文创产品每件进价多3元,购进2件种文创产品和3件种文创产品共需花费26元.(1)、求种文创产品每件的进价;(2)、小张决定购进A , B两种文创产品共100件,且总费用不超过550元,那么小张最多可以购进多少件种文创产品?18. 种下绿色希望,建设美丽辽宁.某学校学生积极参与春季义务植树活动,在活动结束后,该学校为了解八年级学生植树棵数的情况,随机抽取若干名八年级参加植树的学生,统计每人的植树棵数,并对数据进行整理、描述和分析,部分信息如下:
抽取的八年级学生植树棵数的人数统计表
棵数/棵
1
2
3
4
5
人数/人
4
10
6
抽取的八年级学生植树棵数的人数扇形统计图

请根据以上信息,解答下列问题:(1)、求的值;(2)、求被抽取的八年级学生植树棵数的中位数;(3)、本次植树活动中,植树不少于4棵的学生将被学校评为“绿动先锋”,该学校八年级有40名学生参加了此次植树活动,请你估计这些学生中被评为“绿动先锋”的人数.19. 为方便悬挂电子屏幕,学校需要在校门上方的抛物线形框架结构上增加立柱.为此,某数学兴趣小组开展了综合与实践活动,记录如下:活动主题
为校门上方的抛物线形框架结构增加立柱
活动准备
1.去学校档案馆查阅框架结构的图纸;
2.准备皮尺等测量工具.
采集数据
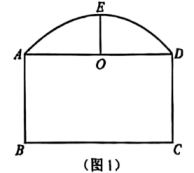
图1是校门及上方抛物线形框架结构的平面示意图,信息如下:
1.大门形状为矩形(矩形);
2.底部跨度(的长)为
;3.立柱的长为 , 且 , 垂足为 .
设计方案
考虑实用和美观等因素,在间增加两根与垂直的立柱,垂足分别为 , 立柱的另一端点在抛物线形框架结构上,其中 .
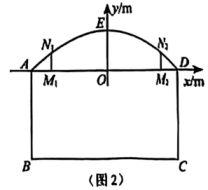
确定思路
小组成员经过讨论,确定以点为坐标原点,线段所在直线为轴,建立如图2所示的平面直角坐标系.点的坐标为(0,2),设抛物线的表达式为 , 分析数据得到点或点的坐标,进而求出抛物线的表达式,再利用表达式求出增加立柱的长度,从而解决问题.
根据以上信息,解决下列问题:
(1)、求抛物线的表达式;(2)、现有一根长度为的材料,如果用它制作这两根立柱,请你通过计算,判断这根材料的长度是否够用(因施工产生的材料长度变化忽略不计)20. 如图,在平面直角坐标系中,直线与轴相交于点 , 与轴相交于点 , 点在线段上(不与点 , 重合),过点作的垂线,与直线相交于点 , 点关于直线的对称点为 , 连接 .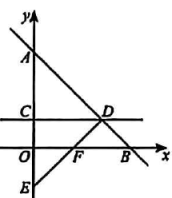 (1)、求证:(2)、设点的坐标为(0,),当时,线段与线段相交于点 , 求四边形面积的最大值.21. 如图,在中, , 以为直径作 , 与相交于点 . 连接 , 与相交于点 .
(1)、求证:(2)、设点的坐标为(0,),当时,线段与线段相交于点 , 求四边形面积的最大值.21. 如图,在中, , 以为直径作 , 与相交于点 . 连接 , 与相交于点 . (1)、如图1,连接 , 求的度数;(2)、如图2,若点为的中点,且 , 求的长.22. 如图
(1)、如图1,连接 , 求的度数;(2)、如图2,若点为的中点,且 , 求的长.22. 如图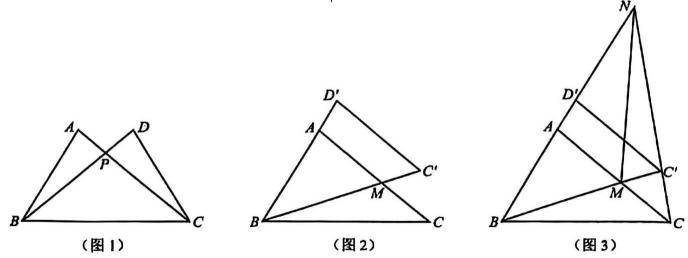 (1)、如图1,在与中,与相交于点 , , 求证:;(2)、如图2,将图1中的绕点逆时针旋转得到 , 当点的对应点在线段的延长线上时,与相交于点:若 , 求的长;(3)、如图3,在(2)的条件下,连接并延长,与的延长线相交于点 , 连接 , 求的面积.23. 如图,在平面直角坐标系中,二次函数的图象与轴的正半轴相交于点 , 二次函数的图象经过点 , 且与二次函数的图象的另一个交点为 , 点的横坐标为 .
(1)、如图1,在与中,与相交于点 , , 求证:;(2)、如图2,将图1中的绕点逆时针旋转得到 , 当点的对应点在线段的延长线上时,与相交于点:若 , 求的长;(3)、如图3,在(2)的条件下,连接并延长,与的延长线相交于点 , 连接 , 求的面积.23. 如图,在平面直角坐标系中,二次函数的图象与轴的正半轴相交于点 , 二次函数的图象经过点 , 且与二次函数的图象的另一个交点为 , 点的横坐标为 .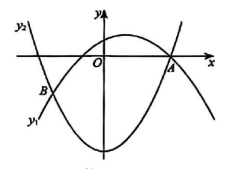 (1)、求点的坐标及的值.(2)、直线与二次函数的图象分别相交于点 , 与直线相交于点 , 当时,
(1)、求点的坐标及的值.(2)、直线与二次函数的图象分别相交于点 , 与直线相交于点 , 当时,①求证:;
②当四边形的一组对边平行时,请直接写出的值.
(3)、二次函数与二次函数组成新函数 , 当时,函数的最小值为 , 最大值为 , 求的取值范围.