浙江省台州市天台县2024-2025学年七年级下学期期末调测数学试题

试卷更新日期：2025-07-08 类型：期末考试

进入 出卷网 下载

一、选择题(本题有10小题，每小题3分，共30分，每小有且只有一个选项是正确的，不选、多选、错选均不给分)1. 下列哪组数是方程 rId5 的解（ ）

  • 1.  下列哪组数是方程 x+y=2 的解（    ）
    A、{x=1y=1 B、{x=1y=−1 C、{x=−1y=1 D、{x=−1y=−1

    查看试题解析

  • 2.  碳纳米管是一种前沿纳米材料，某种碳纳米管的直径是12纳米.已知1纳米=10−9米，那么这种碳纳米管的直径用科学记数法可以表示为（    ）
    A、12×10−6米 B、1.2×10−8米 C、0.12×10−7米 D、0.012×10−6米

    查看试题解析

  • 3.  将数据 80，83，83，84，85，86，86，87，88，89，90 分组，则 86.5~88.5 这一组的频数是（    ）
    A、1 B、2 C、3 D、4

    查看试题解析

  • 4.  下列计算正确的是（    ）
    A、x2⋅x2=2x2 B、x2+x2=2x2 C、(y3)2=y9 D、a9÷a3=a3

    查看试题解析

  • 5.  下列从左到右的变形中，属于因式分解的是（    ）
    A、x(x−1)=x2−x B、x2−x=x(x−1) C、(x+y)(x−y)=x2−y2 D、x2−2x+2=(x−1)2+1

    查看试题解析

  • 6.  若 x+y=2xy ， 则分式 3x+3y−xyxy 的值为（    ）
    A、2 B、3 C、4 D、5

    查看试题解析

  • 7.  将长方形纸带按如图所示折叠，若∠1=70° ， 则∠a的度数为（    ）

    A、40° B、50° C、55° D、60°

    查看试题解析

  • 8. 《九章算术》中记载了一个称重问题：5只麻雀、6只燕子分别放在天平秤上，麻雀一端重，燕子一端轻.麻雀、燕子从两端各交换1只，天平秤就平衡.已知麻雀、燕子总重1斤.问：麻雀、燕子每只重多少？设每只麻雀重x斤，每只燕子重y斤，则可列方程组为（    ）
    A、{5x=6y5x+6y=1 B、{5x−y=6y−x5x+6y=1 C、{4x+y=5y+x5x+6y=1 D、{5x+y=6y+x5x+6y=1

    查看试题解析

  • 9.  图1是某汽车销售店1~4月份的汽车总销量的统计图，图2是其中A品牌的新能源车销量的分析统计图，下列对汽车销售店的销售情况分析错误的是（    ）

    A、4个月共销售汽车300辆 B、1~4月份A品牌新能源车的销量在汽车总销量中的占比呈增长趋势 C、1~4月份A品牌新能源车的销量一直在增长 D、4月份A品牌新能源车销量最高

    查看试题解析

  • 10.  如图，在科学《光的反射》活动课中，老师将支架平面镜放置在水平桌面上，镜面AB延长线与地面的夹角∠ACM=60° ， 激光笔发出的光束DE射到平面镜后，形成反射光束EF. 由科学原理可知：∠CED=∠AEF ， 若反射光束与天花板的夹角∠EFP=70° ， 且PQ//MN ， 则∠CED的度数为（    ）

    A、40° B、50° C、60° D、70°

    查看试题解析

二、填空题(本题有6小题，每小题3分，共18分)

  • 11.  若分式1x−3有意义，则实数x的取值范围为.

    查看试题解析

  • 12. 分解因式： x2 －9= ．

    查看试题解析

  • 13.  2025年全国两会提出“体重管理年”，为了解某校七年级学生的体重情况，从中抽查100名学生的体重进行统计分析，那么这次抽样调查的样本容量是.

    查看试题解析

  • 14.  下面是解方程组{x+y=53x−2y=5的过程导图：

    其中，“ ? ”处为.

    查看试题解析

  • 15.  当m=时，解分式方程：xx−2+1=m2−x会产生增根.

    查看试题解析

  • 16.  一个大长方形由4个正方形①、②、③、④和1个小长方形⑤组成. 已知大长方形面积等于48，正方形④的面积等于1，则正方形①与正方形③的面积之和为.

    查看试题解析

三、解答题(本题有8小题，第17~21题每题8分，第22~23 题每题10分，第24题 12 分，共 72 分)

  • 17.  解方程组：{x=2yx+y=6

    查看试题解析

  • 18.  计算：
    (1)、 20250+2−1；
    (2)、 (x+1)2−x(x+2).

    查看试题解析

  • 19.  如图，已知BE平分∠ABC ， 且∠1=∠2.试判断DE与BC是否平行，并说明理由.

    查看试题解析

  • 20.  在化简分式2aa2−1−1a+1时，一位同学的解答过程如下：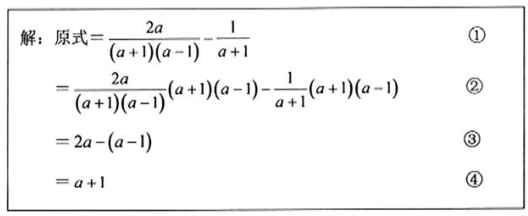

    (1)、该同学的解答从第步开始出错（填序号）；
    (2)、 请写出正确的完整解答过程.

    查看试题解析

  • 21.  如图，在 5×5 的正方形网格中，每个小正方形的边长为 1，其顶点称为格点，格点三角形 ABC 与点 D 的位置如图所示.

    (1)、平移格点三角形 ABC，画出平移后的格点三角形 DEF（点 A，B，C 的对应点分别为点 D，E，F）.
    (2)、请直接写出三角形 DEF 的面积 .

    查看试题解析

  • 22.  为落实“保障中小学生每天校园体育活动时间不低于2小时”政策，某校随机抽查部分学生，对他们喜爱的体育项目展开问卷调查（每人只能选择其中的一项），并将调查数据整理后绘制如下两幅统计图. 请根据图中信息解答下列问题：

    (1)、 求参与问卷调查的学生总人数；
    (2)、 全校共有学生800名学生，根据统计信息，估计该校喜欢乒乓球的男生人数；
    (3)、 小杨同学认为参与问卷调查中喜爱篮球和羽毛球的人数相同，由此可以估计全校喜爱篮球和羽毛球的人数大致相同. 你认为这个说法正确吗？请简要说明理由.

    查看试题解析

  • 23.  三角板 ABC 与三角板 DEF 如图 1 所示摆放，其中 ∠ABC=30° ， ∠DFE=45° ， MN∥PQ ， 点 A，C 在直线 MN 上，点 E，F 在直线 PQ 上。固定三角板 ABC，将三角板 DEF 向右平移.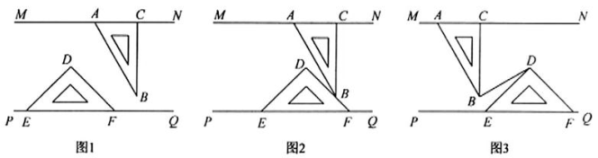

    (1)、 如图 2，当点 B 落在线段 DF 上时，求 ∠ABD 的度数；
    (2)、 在三角板 DEF 平移过程中，连接 BD，记 ∠ABD 为 α ， ∠BDF 为 β.

    ① 如图 1，当点 D 在直线 BC 左侧时，α−β 的值是否为定值，若是定值，请求出这个值；若不是定值，请说明理由.

    ② 如图 3，继续向右平移三角板 DEF，当点 B 在直线 DE 左侧时，第①题中结论是否仍成立？请说明理由.

    查看试题解析

  • 24.  如图，共享单车停放点 A，B 和电影院 C 依次在同一自西向东的道路上.小天和小台从两停放点之间的 P 点同时出发，去往 3060 米远的电影院.小天先步行 3 分钟到停放点 A，然后骑共享单车去往电影院；小台先步行 6 分钟到停放点 B，然后骑共享单车去往电影院.已知两人步行速度均为 60 米/分，小天的骑车速度是小台骑车速度的 0.9 倍，两人同时到达电影院.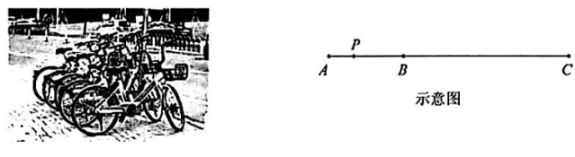

    (1)、 求停放点 A，B 之间的距离；
    (2)、 请分别求出小天和小台的骑车速度；
    (3)、 小山同学在线段 AC 之间的 Q 处，当他得知小天和小台已经出发 1 分钟后，马上走到离他最近的共享单车停放点，骑车赶往电影院，结果三人同时到达电影院.已知小山的步行速度为 70 米/分，他骑车速度与小天相同.求小山出发点 Q 和电影院 C 之间的距离.

    查看试题解析