浙江省杭州市西湖区2024-2025学年第二学期七年级期末教学质量调研数学试题卷

试卷更新日期：2025-07-07 类型：期末考试

进入出卷网下载

一、选择题:本大题有10个小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的.

1. $2^{- 1}$ =( )

A、-2 B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
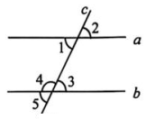
2. 要使分式 $\frac{3}{x - 2}$ 有意义，则 $x$ 的取值应满足（）

A、 $x = 2$ B、 $x \neq 2$ C、 $x = 0$ D、 $x \neq 0$

查看试题解析
3. 要了解某地三个片区共2.7万名初中生的视力情况，某兴趣小组的同学制定了如下调查方案，最合理的是（）

A、抽取某一片区的七年级学生进行调查 B、抽取三个片区的九年级学生进行调查 C、抽取某所学校的所有学生进行调查 D、按片区各抽取3所学校，对9所学校的所有学生进行调查

查看试题解析
4. 如图，直线 $a$ ， $b$ 被直线 $c$ 所截，若要使 $a ∥ b$ ，则需具备条件（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 3 + ∠ 4 = 18 0^{°}$ C、 $∠ 1 = ∠ 4$ D、 $∠ 1 + ∠ 4 = 18 0^{°}$

查看试题解析
5. 下列各式中，运算结果为 $4 a^{6}$ 的是（）

A、 $(- 2 a^{3})^{2}$ B、 $a^{3} \cdot (- 2 a)^{2}$ C、 $2 a^{3} + 2 a^{3}$ D、 $4 a^{6} \div a$

查看试题解析
6. 若 $a - b = - 2$ ， $a b = 3$ ，则 $a^{3} b - 2 a^{2} b^{2} + a b^{3}$ 的值为（）

A、-12 B、-6 C、12 D、6

查看试题解析
7. 《孙子算经》中有这样一道题：今有木，不知长短，引绳度之，余绳四尺五寸，屈绳量之，不足一尺，问几何. 意思是：用一根绳子去量一根木头，绳子剩余4.5尺，将绳子对折再量木头，木头剩余1尺，问木头长多少尺. 设绳子长x尺，木头长y尺，可列出方程组（）

A、 ${\begin{array}{l} x - y = 4.5, \\ y - \frac{1}{2} x = 1 . \end{array}$ B、 ${\begin{array}{l} x - y = 4.5, \\ \frac{1}{2} x - y = 1 . \end{array}$ C、 ${\begin{array}{l} y - x = 4.5, \\ 2 y - x = 1 . \end{array}$ D、 ${\begin{array}{l} y - x = 4.5, \\ 2 x - y = 1 . \end{array}$

查看试题解析
8. 如图，直线 AB， CD 与直线 l 分别交于点 E， F， $∠ B E F$ 的平分线 EG 交 CD 于点 G， $F H ⊥ E G$ 于点 H. 若 $A B ∥ C D$ ，则( )

A、 $∠ E F G = ∠ E G F$ B、 $∠ E F H = ∠ G F H$ C、 $∠ A E G = ∠ C F E$ D、 $∠ B E H + ∠ D F H = 10 0^{°}$

查看试题解析
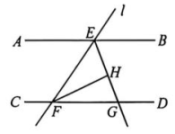9. 近年来，我国新能源汽车产业实现高质量发展. 上图是2018-2023年我国汽车销量和新能源汽车销量折线统计图，则（）

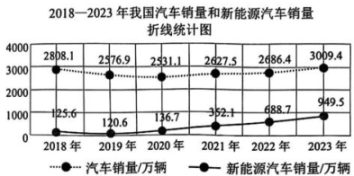A、2018-2023年新能源汽车销量一直保持增长 B、2020-2023年新能源汽车销量的年增长率持续增大 C、2020-2021年新能源汽车销量的年增长率最大 D、2022年新能源汽车销量占当年汽车销量的比例最大

查看试题解析
10. 如图，正方形 ABCD 与正方形 CEFH 的面积和为 58，点 C 在线段 BE 上，点 H 在线段 CD 上，延长 FH 交 AB 于点 G. 若 $B E = 10$ ，则长方形 BCHG 的面积为（）

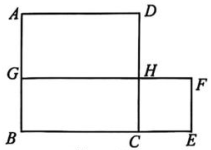A、21 B、24 C、34 D、42

查看试题解析

二、填空题:本大题有6个小题，每小题3分，共18分

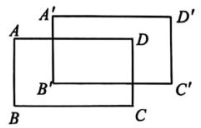
11. 分解因式： $x^{2}$ －9= ．

查看试题解析
12. 如图，将长方形 ABCD 先向右平移 2 个单位长度，再向上平移 1 个单位长度，得到长方形 A'B'C'，若 $A B = 3$ ， $B C = 6$ ，则重合部分的面积为.

查看试题解析
13. 如图，是某市今年连续30天中晴天、阴天、雨天天数的扇形统计图，则晴天有天.

查看试题解析
14. 已知 $x + y = 3 x y$ ，则分式 $\frac{3 x - 2 x y + 3 y}{x + x y + y}$ 的值为.

查看试题解析
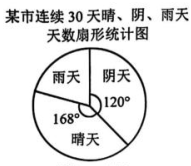15. 一个圆柱形容器中装有一定量的水，放入若干个大铁球和小铁球后（假设所有球都浸没在水中），水面上升情况如图所示，要使水面高度为21，则可以放入个大铁球和个小铁球.（写出一组符合要求的值即可）

查看试题解析
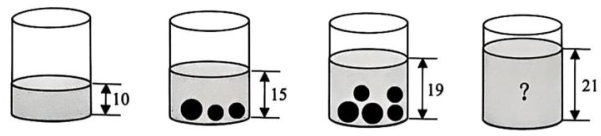16. 如图，将长方形纸片ABCD沿MN折叠得到图1，再沿PM折叠得到图2，已知 $A B ∥ C D$ ， $A M > D N$ .
①如图1，若 $∠ E P N = 5 0^{°}$ ，则 $∠ A M N$ 的度数为 $°$ ；
②如图2，若 $∠ A M G = k ∠ C N M$ ，则 $∠ C P M$ 的度数为 $°$ （用含k的代数式表示）.

查看试题解析

三、解答题:本大题有8个小题，共72分，解答应写出文字说明、证明过程或演算步骤

17. 解方程或方程组.

(1)、 ${\begin{array}{l} 3 x + y = - 1, \\ 2 x - y = 6 . \end{array}$

(2)、 $\frac{2 x - 3}{x + 6} = \frac{1}{2}$ .

查看试题解析
18.

(1)、计算： $\frac{3 x + 2 y}{x^{2} - y^{2}} - \frac{x}{x^{2} - y^{2}}$ .

(2)、当 $x = - 3$ 时，求代数式 $(2 x + 1)^{2} - (2 x - 5) (2 x + 5)$ 的值.

查看试题解析
19. 为了解某校七年级男生的耐力情况，某兴趣小组随机抽取了该年级部分男生的1000m跑成绩，将所得数据进行整理，分成 $A (3^{'} 30 " \leq x < 3^{'} 35 ")$ ， $B (3^{'} 35 " \leq x < 3^{'} 40 ")$ ， $C (3^{'} 40 " \leq x < 3^{'} 45 ")$ ， $D (3^{'} 45 " \leq x < 3^{'} 50 ")$ ， $E (3^{'} 50 " \leq x < 3^{'} 55 ")$ 五组，并绘制成如图所示的未完成的频数表与频数分布直方图（每一组含前一个边界值，不含后一个边界值）.
抽取的男生1000m跑成绩频数表
组别
频数
频率
A
3
a
B
6
0.1
C
12
0.2
D
b
c
E
15
0.25
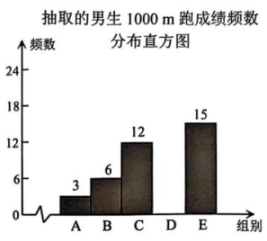
请根据所给信息，解答下列问题：

(1)、填空： $a$ = ， $b$ = ， $c$ =.

(2)、补全频数分布直方图.

(3)、若该校七年级有800名男生，请根据样本估计1000m跑成绩在3'45”(不含3'45”)内的男生人数.

查看试题解析
20. 如图，已知直线 l与直线 AB，CD 分别交于点 E，F， $E G ⊥ C D$ 于点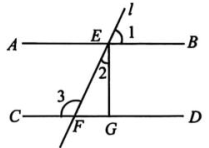 G， $∠ 1$ 与 $∠ 2$ 互余.

(1)、判断直线 AB 与 CD 的位置关系，并说明理由.

(2)、若 $∠ 1 = 3 ∠ 2$ ，求 $∠ 3$ 的度数.

查看试题解析
21. 定义关于*的一种运算： $a * b = a^{b} + a b (a \neq 0 ， b$ 是整数)，例如： $(- 1) * 3 = (- 1)^{3} + (- 1) \times 3 = - 1 - 3 = - 4$ .

(1)、求 $(- 4) * 2$ 的值.

(2)、若 $a * 2 = 1$ ，求 $a * (- 1)$ 的值.

查看试题解析
22. 综合与实践
【问题情境】
自行车的尾灯自身并不发光，但当强光照射到尾灯上时光线会被强烈地反射回去，从而起到提醒汽车驾驶员的目的. 这一效果正是利用了角反射器的原理. 最简单的角反射器是由两个互相垂直的平面镜组成的.
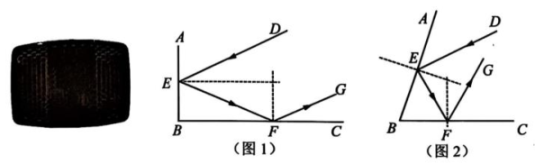
【数学探究】
如图，入射光线DE经过两次反射后，得到光线FG，已知 $∠ A E D = ∠ B E F$ ， $∠ E F B = ∠ G F C$ .

(1)、如图1，AB，BC是两个互相垂直的平面镜， $∠ A B C = 9 0^{°}$ ，
①若 $∠ A E D = 7 0^{°}$ ，求 $∠ G F C$ 的度数.
②试判断入射光线DE和反射光线FG是否平行，并说明理由.

(2)、如图2，改变镜子位置，设平面镜AB，BC的夹角 $∠ A B C = α (α < 9 0^{°})$ ， $∠ A E D = β$ ， $9 0^{°} < α + β < 18 0^{°}$ ，求 $∠ D E F + ∠ E F G$ 的值（用含有 $α$ 或 $β$ 的代数式表示）.

查看试题解析
23. 为了增强学生体质，某校新增了羽毛球、乒乓球两大社团，现要购买一批羽毛球拍和乒乓球拍。已知购买2个羽毛球拍和3个乒乓球拍共需195元；购买3个羽毛球拍和2个乒乓球拍共需230元。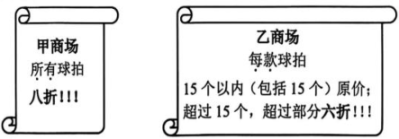

(1)、求羽毛球拍和乒乓球拍的销售单价。

(2)、甲、乙两个商场同时出售这两款球拍，现搞促销活动，海报信息如下：
设学校计划购买a个羽毛球拍，b个乒乓球拍，且两种球拍数量都大于15个，
①请分别计算参加每个商场促销活动的付款金额（用含a，b的代数式表示）.
②若付款金额相等，求a，b满足的数量关系.

查看试题解析
24. 将两张边长分别为a和b（ $a > b$ ）的正方形纸片按图1，图2两种方式放在长方形ABCD内（ $A D > A B$ ），每个正方形都有一组邻边与长方形的边重合.两种放置均有部分重叠，阴影部分是未被这两张正方形纸片覆盖的部分，记图1阴影部分的周长和面积分别为 $C_{1}$ 和 $S_{1}$ ，图2阴影部分的面积为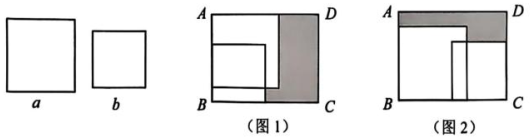 $S_{2}$ .

(1)、若 $A D = 2 b = 16$ ， $A B = 12$ ， $a = 10$ ，直接写出 $C_{1}$ 的值.

(2)、若 $A D - A B = 5$ ， $b = 2$ ，求 $S_{1} - S_{2}$ 的值.

(3)、已知长方形ABCD的周长为36，面积为80， $C_{1} = 28$ ，求 $S_{1} - S_{2}$ 的值.

查看试题解析

组别	频数	频率
A	3	a
B	6	0.1
C	12	0.2
D	b	c
E	15	0.25